
- •Классическая статистическая физика Основные положения
- •Фазовое пространство системы частиц
- •Число степеней свободы
- •«Вымерзание» степеней свободы
- •Размерность фазового пространства
- •Число микросостояний в элементе объема Элемент объема фазового пространства равен
- •Объем и площадь n-мерной сферы
- •Фазовая траектория
- •Фазовый ансамбль
- •Теорема Лиувилля
- •, . (2.5)
- •Следствия теоремы Лиувилля
- •Пример. Идеальный газ двухатомных молекул
- •Микроканоническое распределение Основные понятия и определения
- •Распределение микросостояний по фазовому пространству
- •Энергетическая плотность состояний
- •Пример энергетической плотности состояний
- •Нормировочная постоянная микроканонического распределения
- •Микроканоническое распределение
- •Число микросостояний газа
- •Число микросостояний частицы
- •Энергетическая плотность состояний газа
- •Энергетическая плотность состояний частицы
- •Характеристики макросостояния
- •Вариация числа микросостояний при изменении объема
- •Статистический смысл давления
- •Соотношение между статистическими и термодинамическими характеристиками
- •Статистический смысл температуры
- •Статистический смысл энтропии
- •Пример 1
- •Пример 2
- •Каноническое распределение
- •Распределение микросостояний газа по энергии
- •Макрохарактеристики и статистический интеграл
- •Принцип Ландауэра
- •Статистический интеграл поступательного движения
- •Статистический интеграл колебательного движения
- •Статистический интеграл вращательного движения
- •Теорема Бора – Ван-Лёвен
- •Распределение тепловой энергии по степеням свободы
- •Примеры
- •Вопросы коллоквиума
Классическая статистическая физика Основные положения
Объект
– идеальный
газ независимых микрочастиц, подчиняющихся
классической механике и описываемых
уравнениями
Гамильтона.
Эти уравнения являются законами динамики,
записанными через гамильтониан
– полную энергию, выраженную через
координаты и импульсы частиц. Выбор
этих переменных вызван тем, что
микрочастицы подчиняются законам
квантовой физики. Неопределенности
координат и импульсов частицы связаны
соотношением Гейзенберга
![]() ,
что существенно используется при
статистическом описании даже в рамках
классической физики. Используется также
тождественность микрочастиц.
,
что существенно используется при
статистическом описании даже в рамках
классической физики. Используется также
тождественность микрочастиц.
Задача – найти статистические распределения частиц газа по координатам, импульсам, энергии. Используется метод Гиббса, разработанный в 1902 г.

Джозайя Уиллард Гиббс (1839–1903)
Основные понятия: микросостояние газа, макросостояние газа, фазовое пространство, функция распределения по фазовому пространству.
Микросостояние системы частиц – совокупность координат и импульсов всех частиц газа, зафиксированных в один момент времени. Микросостояние отображает точка X в фазовом пространстве. С течением времени микросостояние изменяется и точка перемещается по фазовому пространству.
Функция
распределения плотности вероятности
![]() – вероятность обнаружения микросостояния
газа в единице объема фазового пространства
около точкиX.
– вероятность обнаружения микросостояния
газа в единице объема фазового пространства
около точкиX.
Статистический интеграл Z – нормировочная постоянная функции распределения.
Макросостояние системы частиц – состояние газа как единого целого. Описывается термодинамическими величинами – температурой Т, давлением Р, внутренней энергией U, свободной энергией F и др. Одно макросостояние реализуется множеством разных микросостояний, образующих фазовый ансамбль. Термодинамическая величина, характеризующая макросостояние, получается усреднением по фазовому ансамблю с использованием функции распределения, и выражается через статистический интеграл Z.
Фазовое пространство системы частиц
Микросостояние системы частиц отображается точкой фазового пространства
![]() ,
,
где
![]() и
и![]() – обобщенные координата и импульс
частицы системы;n
– число степеней свободы системы. Число
n
равно числу проекций координат всех
частиц и пропорционально числу частиц.
Число проекций импульсов равно числу
проекций координат, поэтому число
независимых координат фазового
пространства равно 2n.
Для каждой системы используется свое
фазовое пространство.
– обобщенные координата и импульс
частицы системы;n
– число степеней свободы системы. Число
n
равно числу проекций координат всех
частиц и пропорционально числу частиц.
Число проекций импульсов равно числу
проекций координат, поэтому число
независимых координат фазового
пространства равно 2n.
Для каждой системы используется свое
фазовое пространство.
Координата частицы газа и ее импульс с течением времени изменяются согласно уравнениям Гамильтона
 ,
(2.1а)
,
(2.1а)
 .
(2.1б)
.
(2.1б)

Уильям Гамильтон (1805–1865)
Гамильтониан– полная энергия системы в виде суммы кинетических и потенциальных энергий всех частиц, выраженная через координаты и импульсы частиц:
 .
.
Для
нерелятивистской частицы k
массой
![]() кинетическая энергия
кинетическая энергия
 .
.
Для консервативной системы полная энергия сохраняется
![]()
и микросостояния находятся на гиперповерхности фазового пространства.
Уравнения Гамильтона для одномерного движения частицы. Используем гамильтониан
 .
.
Из уравнения Гамильтона (2.1а)
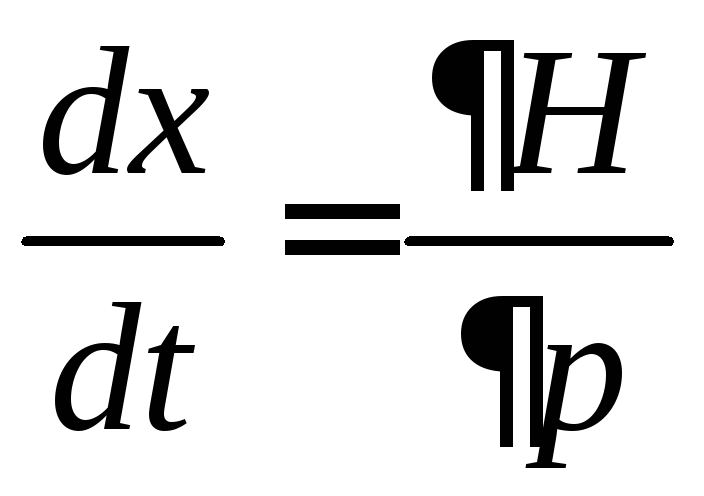
с учетом определения скорости
![]()
получаем известное соотношение между импульсом и скоростью
![]() .
.
Из уравнения Гамильтона (2.1б)
![]()
находим
![]()
– второй закон Ньютона. Уравнения Гамильтона являются унифицированной формой записи известных уравнений механики на основе гамильтониана.
