Случай

Лабораторная работа №31

«Некоторые законы случайных событий»

Выполнили:

Куликов Н. С.

Королёв Н. С.

ВШ ОПФ

2015 г.

Цель работы: исследование законов случайных событий.

Оборудование и материалы: доска Гальтона, пшено (частицы), мерный стакан, линейка, мультиметр, резисторы (R_ном=620 Ом ±10% ) х67 шт.

Теоретическое обоснование:

Случайное событие и случайная величина

Неопределенность исхода опыта при соблюдении основных условий его проведения характерна для широкого круга явлений.

В теории вероятностей наблюдение, производимое при неизменном комплексе контролируемых событий, называется статистическим испытанием. И его исход является случайным событием.

Случайными величинами в случае доски Гальтона будут например траектории движения зерен, количество зерен в ячейке или, например, время полета каждого зерна.

Свойство статистической устойчивости.

Снова рассмотрим доску Гальтона. Допустим зернышко было брошено N раз. За N_k возьмем количество испытаний в которых зернышко попало в K-ую ячейку. Тогда отношение P*(N,k)=N_k/N – относительная частота событий.

Относительная частота – также случайная величина. Однако если провести N независимых одинаковых испытаний, то выяснится, что при большом N относительная частота практически не зависит от N. Именно это называется статистической устойчивостью. Именно она позволяет построить для случайных явлений и величин теорию, предсказывающую результаты многократно повторяемых событий.

С точки зрения математики:

Соответственно величину P(k) называют вероятностью случайного события. Простыми словами это вероятность того, что случайная величина окажется равной K.

Дискретность и непрерывность случайных величин.

Случайная величина, которая может принимать только целое и ограниченное число значений называется дискретной. В случае доски Гальтона – это номер ячейки.

Величины принимающие непрерывный ряд значений называются непрерывными случайными величинам.

Закон распределения случайной величины.

1. Интегральная функция распределения.

Запись распределения случайных величин в виде таблиц неудобна. Значительно удобнее использовать функции распределения.

– интегральная функция распределения.

При этом стоит отметить, что интегральная функция распределения имеет одинаковый смысл как для дискретных величин, так и для непрерывных.

Она обладает следующими свойствами:

1. Монотонно возрастает на всем протяжении.

2. Наименьшее значение принимается при -∞, а наибольшее при +∞.

Т.е.:

Для дискретной случайной величины F(x) она представляет собой кусочно-постоянную функцию, со скачками в точках разрешённых x_k: , при этом

Для интегральной функции будет гладкой и монотонно возрастающей.

Типичные графики таких функций представлены ниже:

2. Дифференциальная функция распределения.

Наряду с интегральной функцией, распределения часто используют дифференциальную функцию распределения или плотность вероятностей. По определению она равна:

При достаточно малом Δx, плотность вероятности будет равна вероятности попадания случайной величины в заданный интервал.

Если же необходимо отыскать вероятность попадания на большой отрезок, пользуются следующей формулой:

Ее смысл очевиден из самого определения дифференциальной функции распределения. Ведь:

Общие свойства плотностей вероятности:

1. Имеет размерность обратную размерности случайной величины X/

2. Плотность вероятностей всегда больше нуля (следует из монотонного возрастания интегральной функции).

3. Выполняется условие:

Среднее значение и дисперсия.

Допустим случайная величина X в N принимает значения x₁,…,x_n. Тогда среднее значение (обозначается чертой сверху):

Перегруппировав:

Среднее же значение непрерывной величины:

Другой важной характеристикой является дисперсия случайной величины:

В инженерных приложениях удобнее использовать не дисперсию а среднеквадратичное отклонение . По-другому её еще называют стандартным отклонением или просто стандартом величины X. Случайные отклонения величины от среднего её значения называются флуктуациями. Относительная флуктуация: .

Закон распределения для доски Гальтона.

В опытах с доской Гальтона при больших количествах частиц вероятность пропорциональна высоте столбика и обратно пропорциональна сумме их высот во всех столбиках. При этом график функции P(k) будет иметь колоколообразную форму. И при достаточно большом количестве ячеек Вероятность приближенно описывается формулой: , где – вероятность попадания в столбик с наибольшей высотой.

В таком случае

Это значит что

Для этой формулы выполняются все необходимые для дифференциального распределения условия.

Кроме того оказывается:

Если же в качестве случайной величины рассматривать не номер ячейки а координату x, то дифференциальная функция распределения будет записываться :

Задание I: Примерная траектория

одного зернышка.

По рисунку очевидно, что траектория зернышка случайна.

Задание II: Серия испытаний с 10 зернами.

	1	2	3		1	2	3		1	2	3
1			1	21				41	1		1
2	1			22				42
3				23		1		43
4				24				44
5	1			25	1			45
6	1			26				46			1
7				27			1	47		1
8				28		1		48
9		1		29				49
10				30				50		1
11				31			1	51			1
12				32	1
13			1	33		1
14				34		1
15	1			35
16				36
17		1		37
18	2		1	38	1
19			1	39			1
20		1		40	1	1

В общем-то эта таблица не даёт никакой информации. Но подтверждает тот факт, что при малом количестве испытаний невозможно составить статистическую картину.

Задание III:

Таблица для половины стакана.

Для упрощения я не строил график для каждого опыта, но построил для средних значений.

Необходимо отметить, что красная линия – прогнозируемая высота столбца в ячейке, зеленые линии по центру «подсвечивают» столбец с максимальной высотой, единичная зеленая линия, перпендикулярная им – отмечает высоту . При этом полученое на графике значение достаточно близко к значению полученному из этой () формулы.

По нему хорошо видно, что для доски Гальтона хорошо выполняется нормальное распределение.

То же для целого стакана.

По нему мы видим примерно то же самое.

Примечание: На самом деле при построении расчётного распределения в качестве высоты столбца бралось не его собственное значение, а значение его и двух соседних элементов, взятых с определенными весовыми коэффициентами, в сумме образующими 1.

Т.е. как и ожидалось почти в 2 раза меньше.

Задание IV:

Выше представлена таблица, полученная в результате прямого измерения сопротивления каждого резистора. На основании этих данных были построены интегральная и дифференциальная функции распределения.

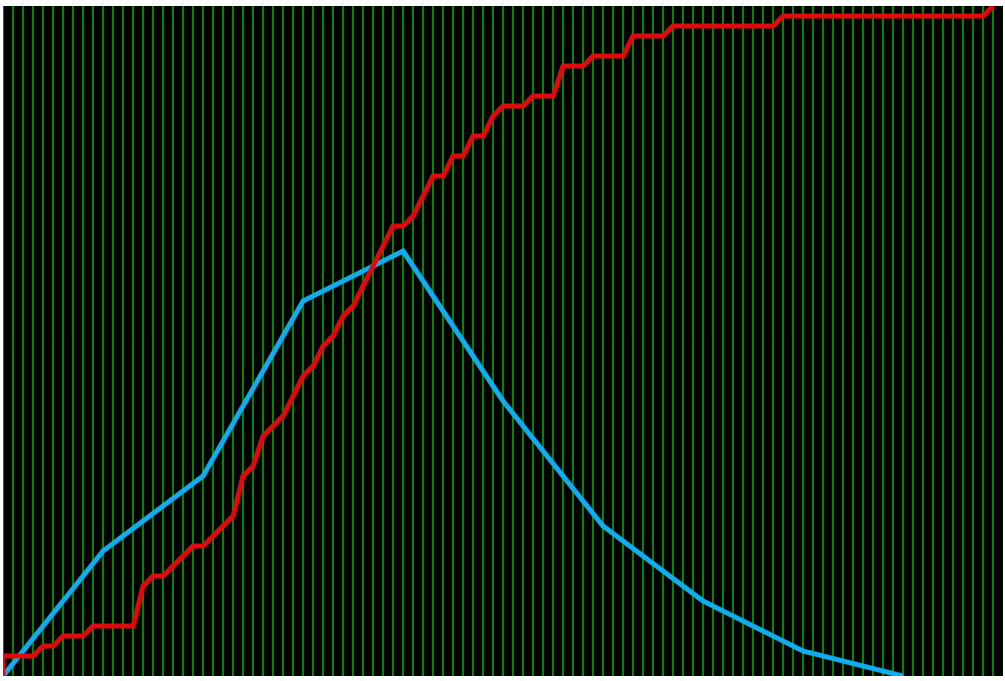
На первом рисунке видна интегральная функция распределения и дифференциальная функция распределения. На втором представлена (в лучшем масштабе) та же дифференциальная функция и сравнение ее с расчётной.

Вывод: нами были исследованы законы случайных событий. Проверено их выполнение на практике и сравнены прогнозируемые и экспериментальные результаты в результате чего была выявлена хорошая связь между ними.

15