- •Санкт-Петербургский университет управления и экономики
- •2014 Оглавление
- •Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •Рекомендуемая литература
- •Краткие теоретические сведения для выполнения контрольной работы № 1 и решение типовых задач
- •1.1. Матрицы и действия над ними
- •Действия над матрицами
- •1.2. Определители 2-го и 3-го порядков
- •Вычисление определителей 2-го и 3-го порядка
- •Свойства определителей
- •1.3. Обратная матрица
- •1.4. Решение систем линейных алгебраических уравнений (слаУр)
- •Формулы Крамера для решения слаУр
- •Рассмотрим матрицу специального вида
- •Метод Гаусса решения слаУр
- •Краткие теоретические сведения для выполнения контрольной работы № 2 и решение типовых задач
- •2.1. Прямая на плоскости
- •Условие параллельности двух прямых
- •Условие перпендикулярности двух прямых
- •2.2. Элементы векторной алгебры и аналитической геометрии в пространстве
- •Краткие теоретические сведения для выполнения контрольной работы № 3 и решение типовых задач
- •3.1. Раскрытие неопределенности вида .
- •3.2. Раскрытие неопределенности вида
- •3.3. Вычисление пределов с использованием второго замечательного предела
- •3.4. Непрерывность функции
- •Классификация точек разрыва
- •3.5. Правила дифференцирования
- •Правила дифференцирования
- •3.6. Производная сложной функции
- •3.7. Метод логарифмического дифференцирования
- •3.8. Производная функции, заданной неявно
- •3.9. Дифференцирование функций, заданных параметрически
- •3.10. Исследование функций и построение графиков функций
- •Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
- •4.1. Метод интегрирования подведением под знак дифференциала
- •4.2. Метод интегрирования по частям
- •4.3. Интегрирование тригонометрических выражений
- •4.4. Вычисление площадей с помощью определенного интеграла
- •1. Элементы линейной алгебры
- •2. Элементы векторной алгебры и аналитической геометрии
- •3. Предел и производная функции одной переменной
- •4. Интегральное исчисление функции одной переменной
Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
4.1. Метод интегрирования подведением под знак дифференциала
Функция
![]() называется первообразной для функции
называется первообразной для функции![]() на
интервале
на
интервале![]() ,
конечном или бесконечном, если в любой
точке
,
конечном или бесконечном, если в любой
точке![]() этого интервала функция
этого интервала функция![]() дифференцируема и имеет производную
дифференцируема и имеет производную![]() .
.
Совокупность
всех первообразных для функции
![]() ,
определенных на интервале
,
определенных на интервале![]() ,
называетсянеопределенным
интегралом
от функции
,
называетсянеопределенным
интегралом
от функции
![]() на этом интервале и обозначается символом
на этом интервале и обозначается символом
![]() .
.
Метод подведения под знак дифференциала следует из свойства инвариантности неопределенного интеграла.
Пусть дан
интеграл
![]() .
Справедливо равенство
.
Справедливо равенство
![]() ,
,
где
![]() – некоторая непрерывно дифференцируемая
функция.
– некоторая непрерывно дифференцируемая
функция.
Таблица интегралов
|
1.
|
8.
|
|
2.
|
9.
|
|
3.
|
10.
|
|
4.
|
11.
|
|
5.
|
12.
|
|
6.
|
13.
|
|
7.
|
14.
|
|
15.
| |
При интегрировании методом подведения под знак дифференциала необходимо иметь в виду следующие равенства:
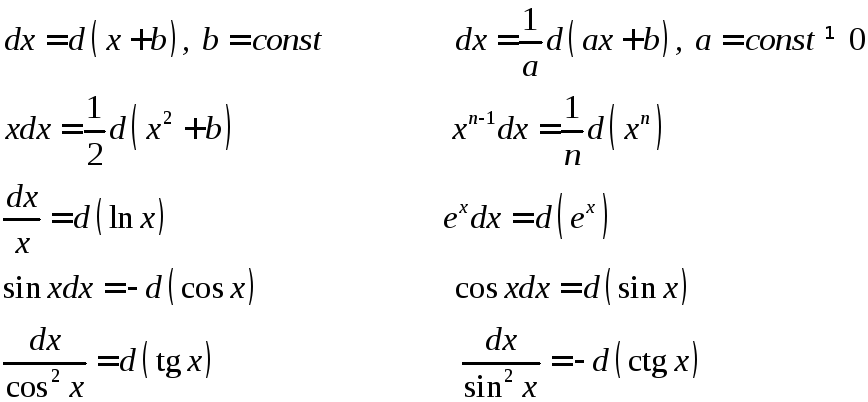
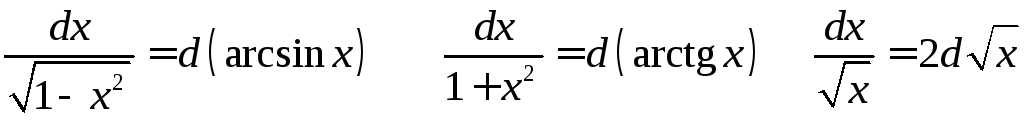
В общем случае
![]() .
.
Пример 1
Найти интеграл![]() .
.
Так как
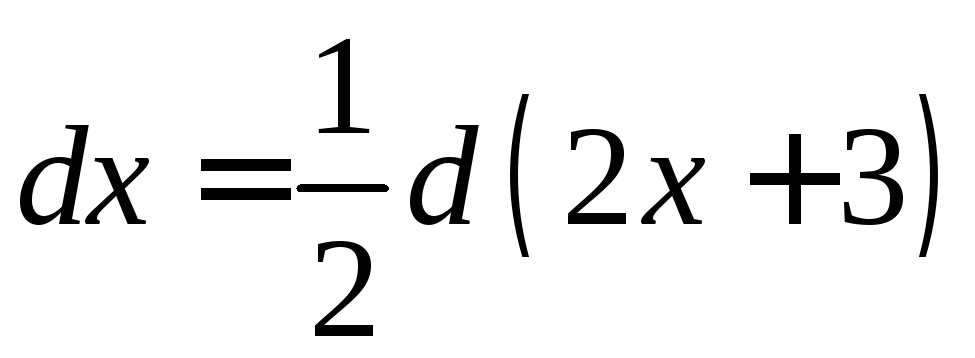 ,
то
,
то
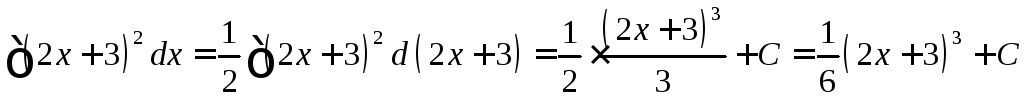 .
.
Пример 2
Найти интеграл
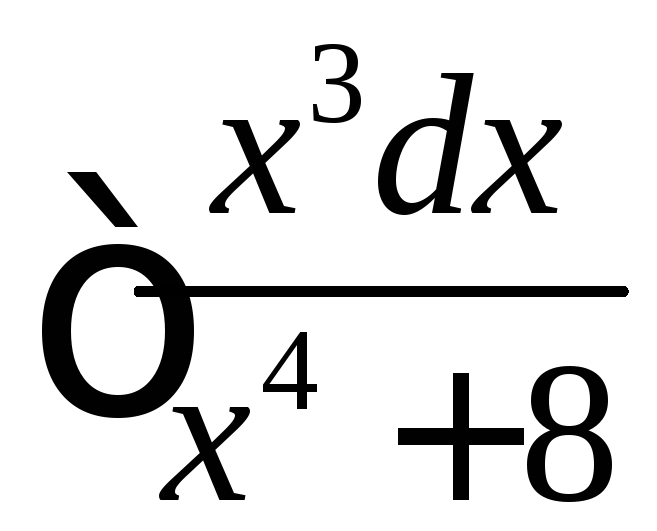 .
.
Так как
 ,
то
,
то
 .
.
Пример 3
Найти интеграл
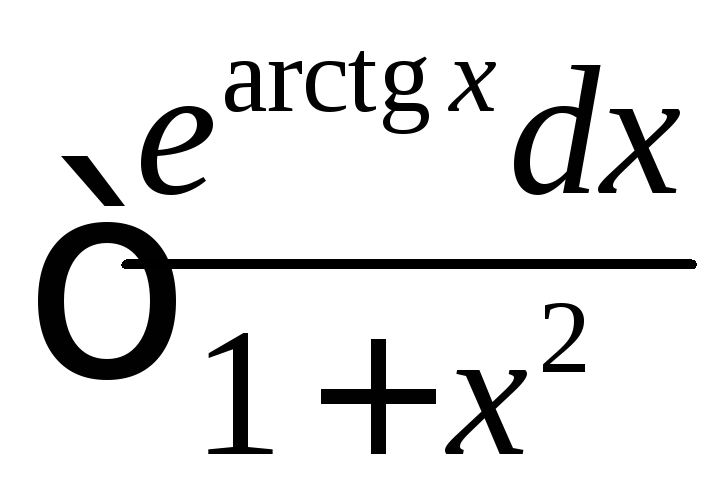 .
.
Так как
 ,
то
,
то
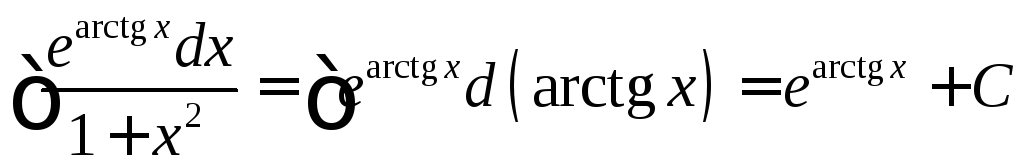
Пример 4
Найти интеграл
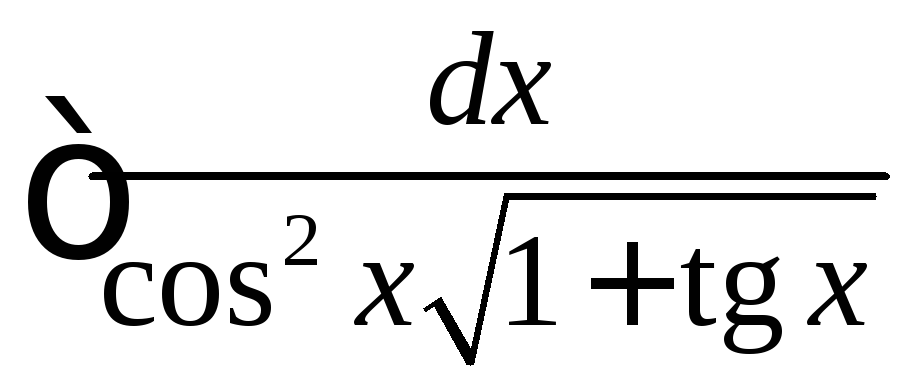 .
.
Так как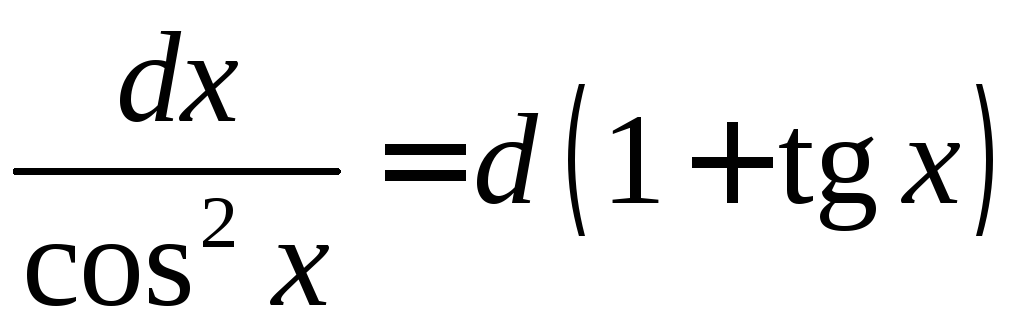 ,
то
,
то
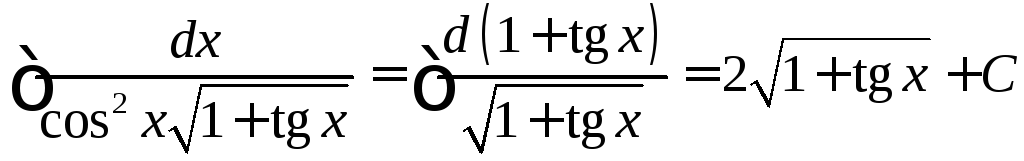 .
.
4.2. Метод интегрирования по частям
Пусть дан интеграл
вида
![]() ,
где
,
где![]() - непрерывно дифференцируемые функции.
Справедлива формула интегрирования по
частям
- непрерывно дифференцируемые функции.
Справедлива формула интегрирования по
частям
![]() .
.
Таким образом,
вычисление интеграла
![]() приводится к вычислению интеграла
приводится к вычислению интеграла![]() ,
который может оказаться более простым
или табличным.
,
который может оказаться более простым
или табличным.
Пусть
![]() - многочлен степениn.
Методом интегрирования по частям можно
вычислить, например, интегралы вида:
- многочлен степениn.
Методом интегрирования по частям можно
вычислить, например, интегралы вида:
|
1 группа: |
2 группа: |
|
|
|
|
|
|
|
|
|
|
|
|
Пример
Найти интеграл
![]() .
.
Решение
Положим
![]() ,
найдем
,
найдем![]() ,
,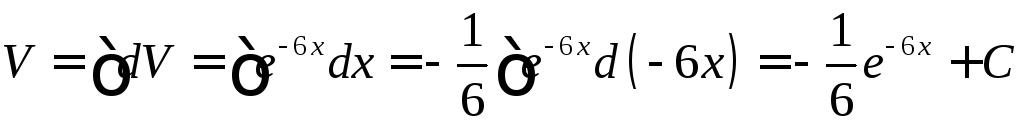 .
Так как достаточно взять одну из
первообразных, то принимаем
.
Так как достаточно взять одну из
первообразных, то принимаем![]() .
Применим формулу интегрирования по
частям
.
Применим формулу интегрирования по
частям
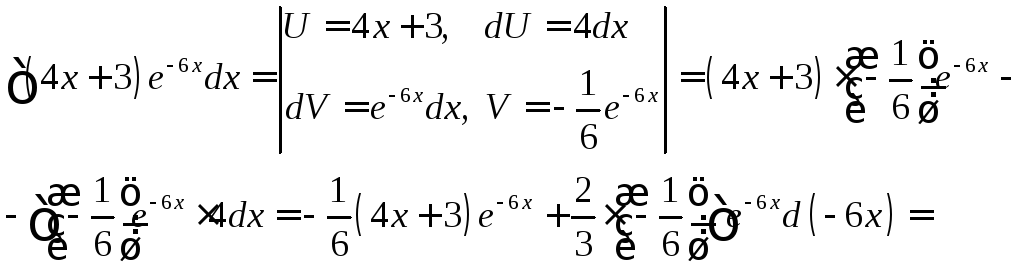
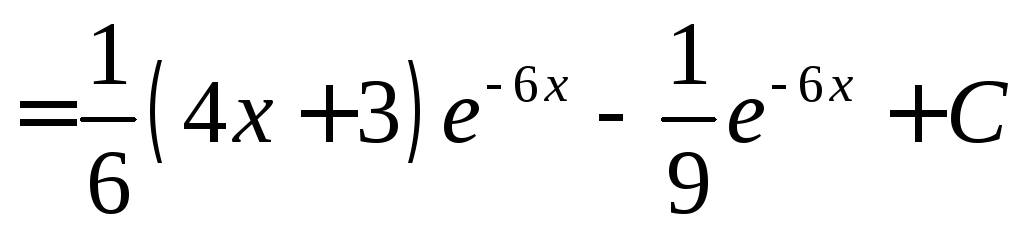 .
.
4.3. Интегрирование тригонометрических выражений
Рассмотрим интеграл
вида
![]() гдеR
– рациональная функция своих аргументов.
гдеR
– рациональная функция своих аргументов.
Универсальная
подстановка
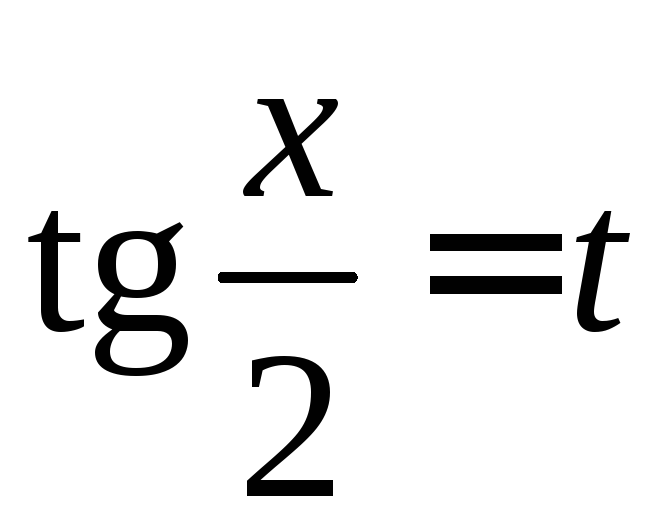 сводит данный интеграл к интегралу от
рациональной дроби, при этом
сводит данный интеграл к интегралу от
рациональной дроби, при этом
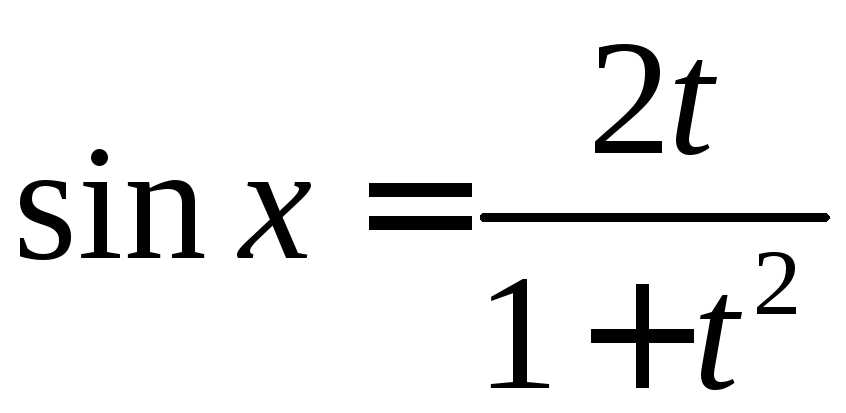 ,
,
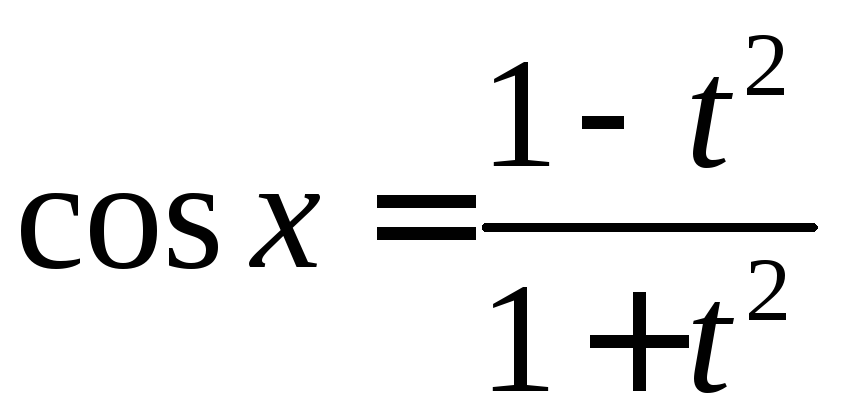 ,
,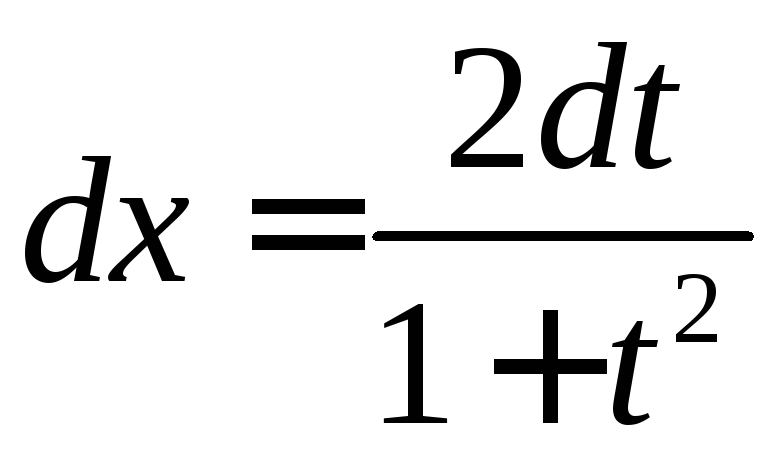 .
.
Итак:
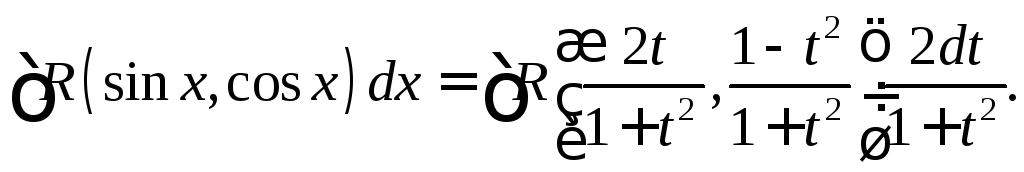
Пример
Найти интеграл
![]() .
.
Решение
Применим универсальную подстановку
 ,
,
получим

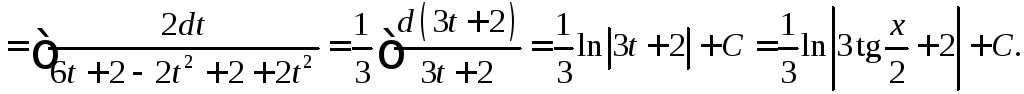
4.4. Вычисление площадей с помощью определенного интеграла
Пусть функция
![]() определена и непрерывная на отрезке
определена и непрерывная на отрезке![]() и пусть, для определенности,
и пусть, для определенности,![]()
Разобьем отрезок
![]() наn
частей произвольным образом точками
деления:
наn
частей произвольным образом точками
деления:
![]() .
Выберем на каждом частичном промежутке
.
Выберем на каждом частичном промежутке![]() произвольным образом точки
произвольным образом точки![]()
![]() .
.
Обозначим
![]() Составим сумму
Составим сумму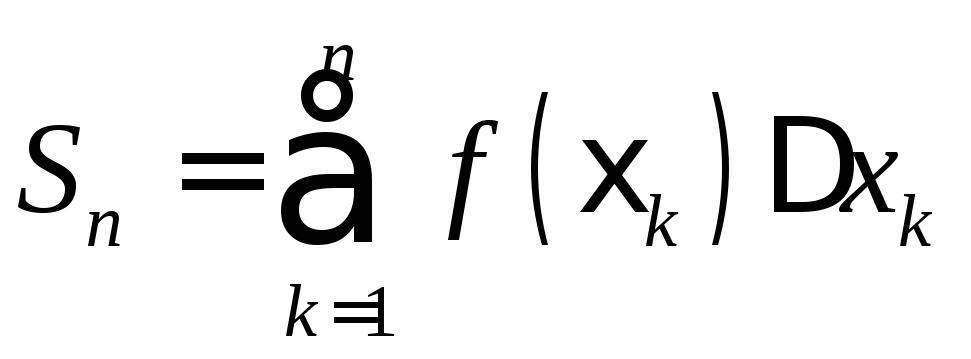 ,
которая называетсяинтегральной
суммой для
функции
,
которая называетсяинтегральной
суммой для
функции
![]() на отрезке
на отрезке![]() .
.
Обозначим длину
наибольшего частичного промежутка
через
![]() Перейдем к пределу при
Перейдем к пределу при![]() .
.
Если существует
конечный предел
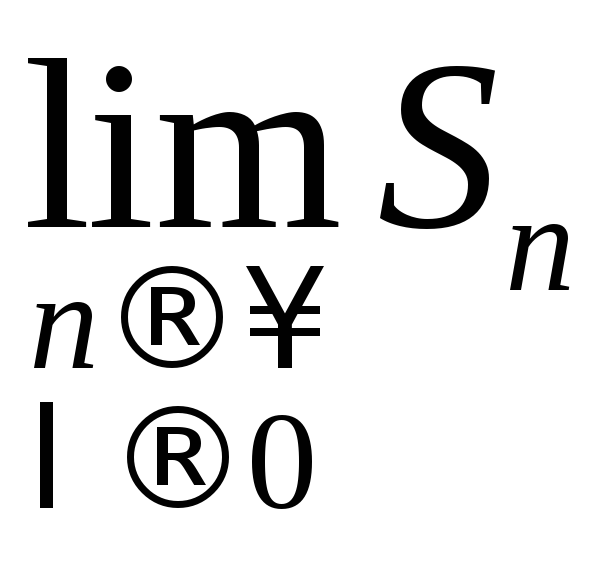 ,
не зависящий от способа разбиения
отрезка
,
не зависящий от способа разбиения
отрезка![]() на частичные и выбора на них точек
на частичные и выбора на них точек![]() ,
то он и называетсяопределенным
интегралом
от функции
,
то он и называетсяопределенным
интегралом
от функции
![]() на отрезке
на отрезке![]() и обозначается
и обозначается
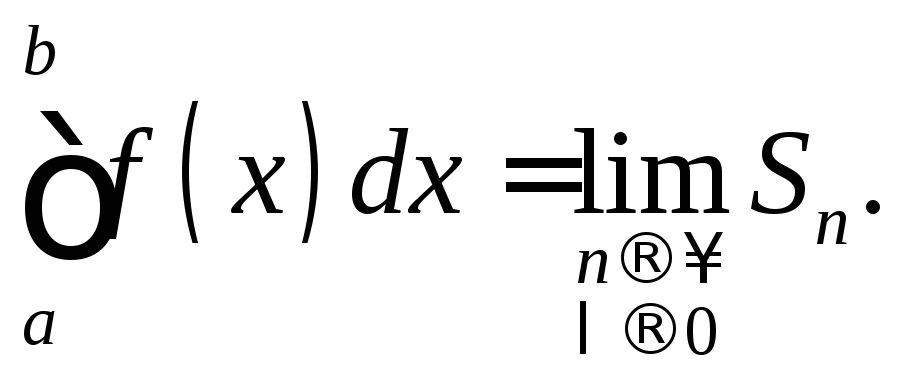
Если
![]() – любая первообразная для функции
– любая первообразная для функции![]() ,
то справедливаформула
Ньютона – Лейбница:
,
то справедливаформула
Ньютона – Лейбница:
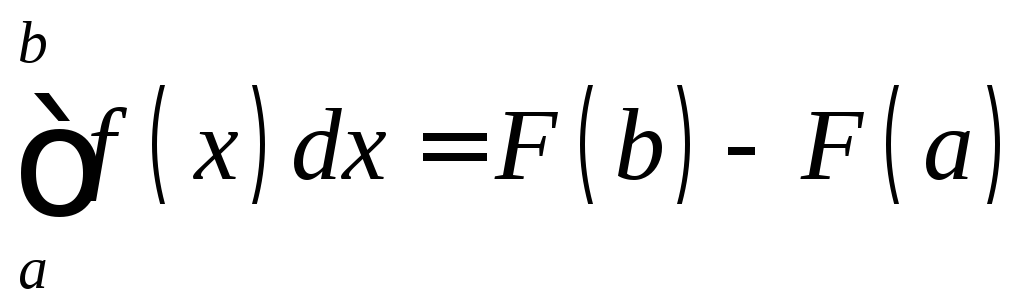 ,
,
т.е. для вычисления
определенного интеграла от непрерывной
функции
![]() нужно составить разность значений
произвольной ее первообразной для
верхнего и нижнего пределов интегрирования.
нужно составить разность значений
произвольной ее первообразной для
верхнего и нижнего пределов интегрирования.
Пример 1
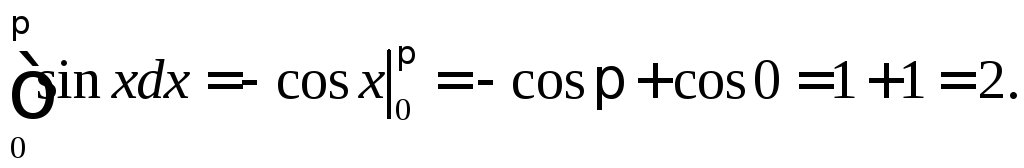
Если
![]() то
то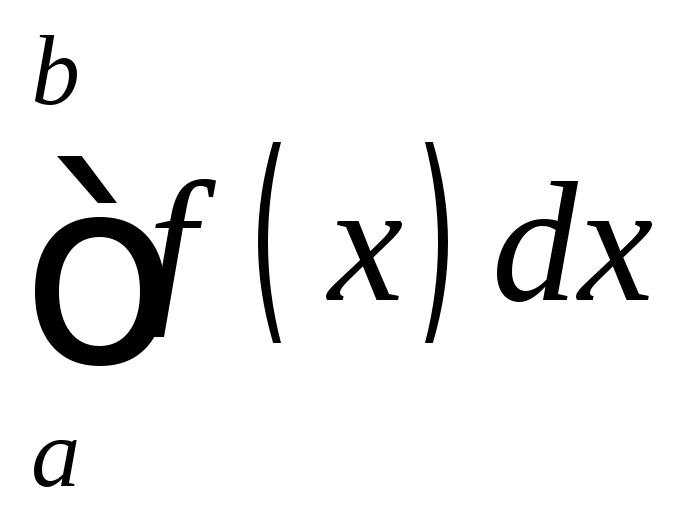 численно равен площади криволинейной
трапеции, ограниченной кривой
численно равен площади криволинейной
трапеции, ограниченной кривой![]() ,
,
прямыми
![]() и осьюох:
и осьюох:
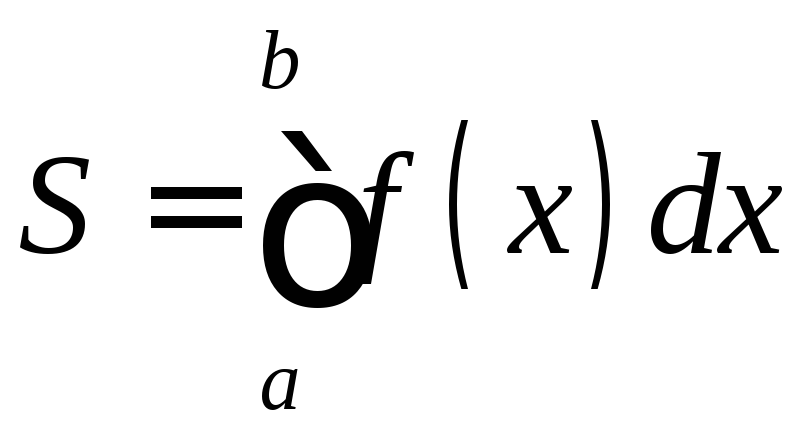
Если
![]() меняет знак конечное число раз на
отрезке
меняет знак конечное число раз на
отрезке![]() ,
то интеграл по всему отрезку разбивается
на сумму интегралов по частичным
отрезкам, интеграл будет положителен
там, где
,
то интеграл по всему отрезку разбивается
на сумму интегралов по частичным
отрезкам, интеграл будет положителен
там, где![]() и отрицателен, где
и отрицателен, где![]() :
:
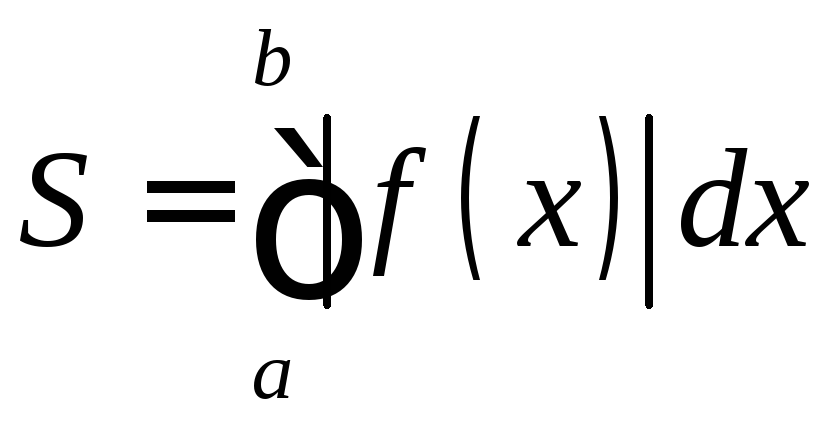 .
.
Пусть нужно
вычислить площадь фигуры, ограниченной
кривыми
![]() и
и![]() и прямыми
и прямыми![]() ,
тогда при условии
,
тогда при условии![]() имеем
имеем
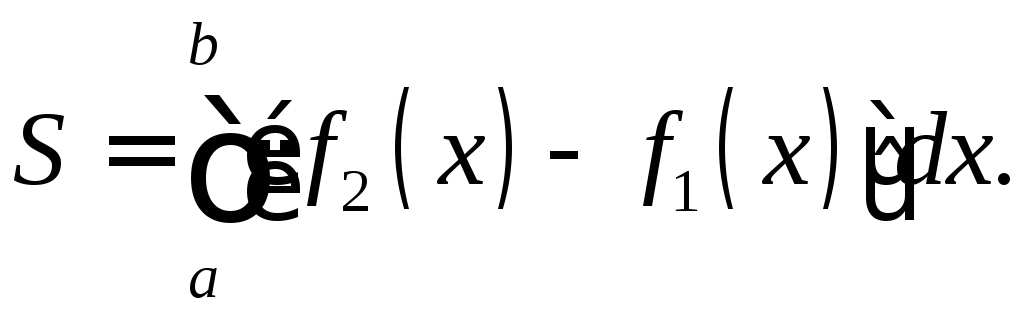
Пример 2
Вычислить площадь
фигуры, ограниченной линиями
![]() и
и![]() .
.
Решение
|
у=х+3
у=х2+1 3
–3 –1 0 2 х
|
Найдем точки
пересечения:
|
 .
.
Краткое содержание (программа) курса



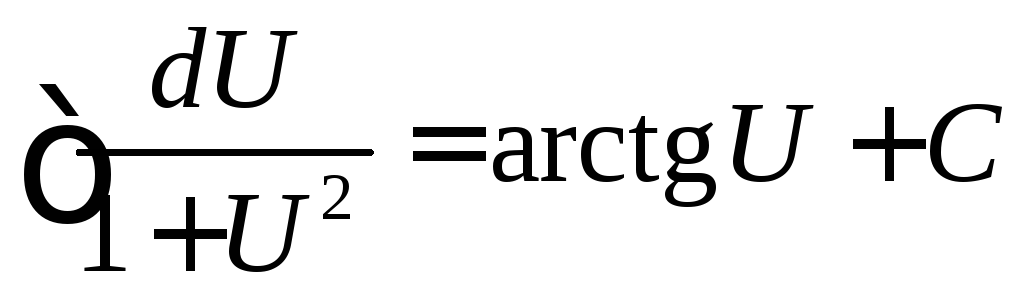
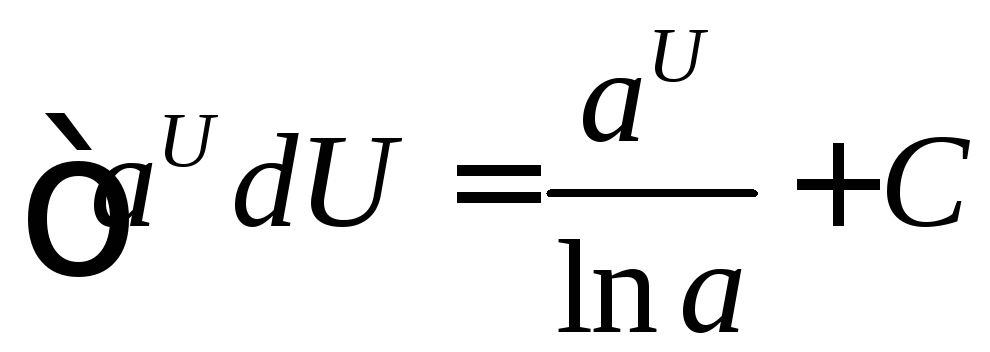
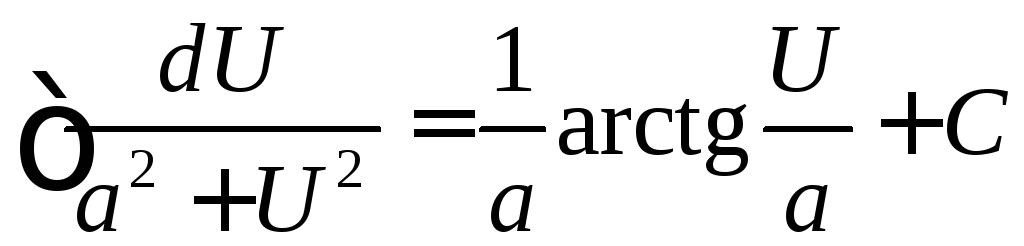
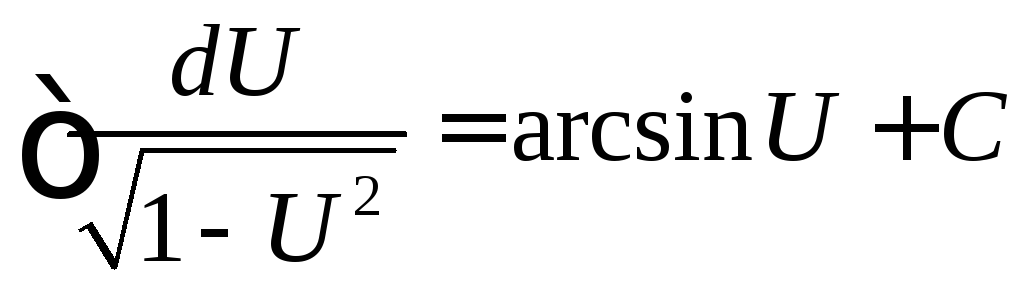
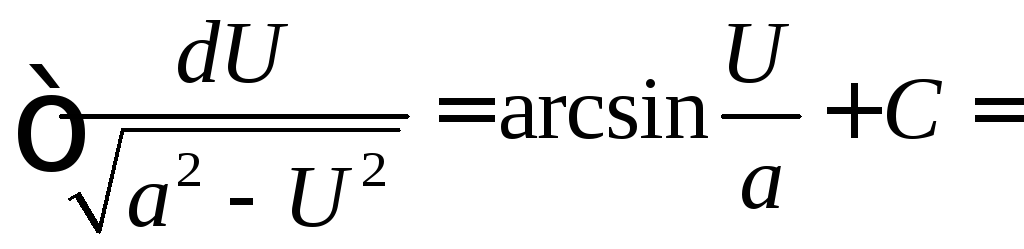
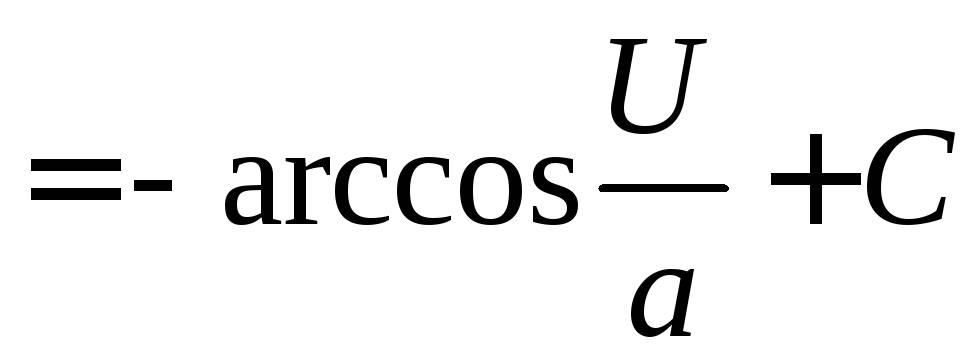






 у
у

 ,
,