42

Лекция 3. Кинематика газа и жидкости

3.1. Основные определения

Кинематика жидкой среды занимается вопросами движения жидкости и газа независимо от причин его возникновения.

Используя представления механики материальной точки можно ввести понятие скорости в заданной точке пространства , которая будет именоваться местной или локальной скоростью.

Изменение скорости по величине и направлению от точки к точке пространства требует ее определения в векторной форме. Вектор локальной скорости и три ее проекции на оси координат оказываются функциями четырех аргументов т. е.

(3.1)

Общий случай, когда скорость зависит от координат и времени называется неустановившимся (нестационарным).

Если скорость жидкости не зависти от времени, то движение называется установившимся (стационарным).

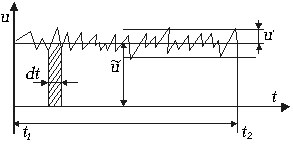
Рис. 3.1. Определение пульсационного движения

В некоторых случаях движение может считаться квазиустановившимся, если зависимость от времени не является существенной. Зависимостью от времени можно пренебречь без понижения точности решения, например, если скорость колеблется в небольших пределах и с достаточной частотой относительно некоторого постоянного значения (рис. 3.1).

За некоторое время осреднения средняя скорость , относительно которой происходят пульсации, равна

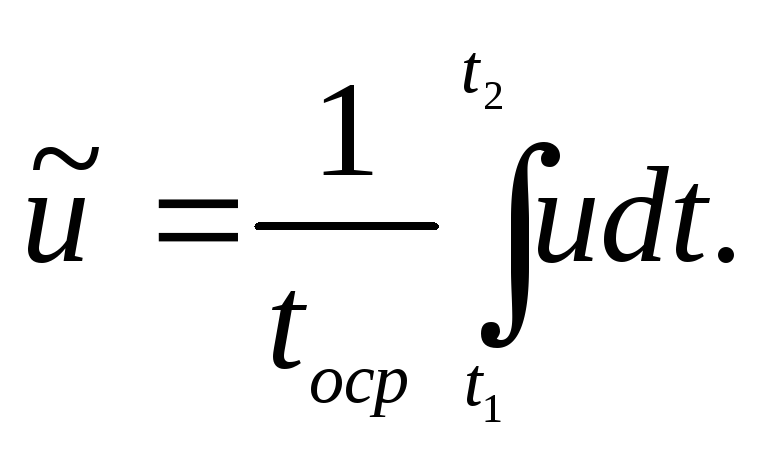(3.2)

Модуль действительной мгновенной скорости будет равен

(3.3)

где пульсационная скорость знакопеременна и подчиняется условию

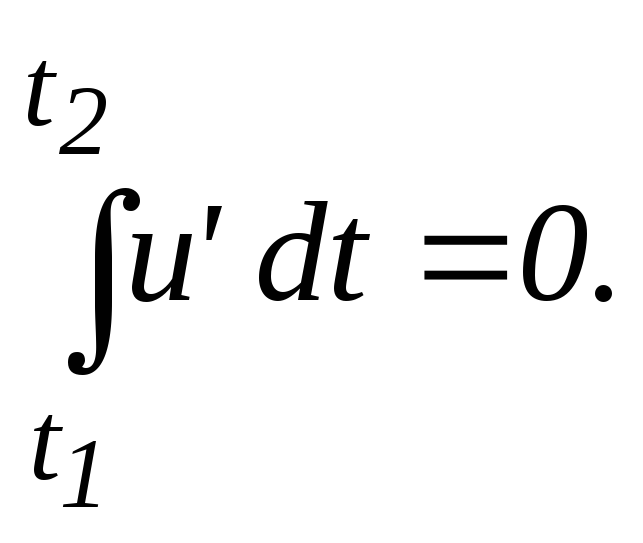(3.4)

Определение может быть распространено на пространственное распределение скоростей, тогда средняя скорость равна

, (3.5)

где - площадь потока жидкости.

При движении жидкости помимо нормальных возникают касательные напряжения, что меняет распределение в пространстве и нормальных напряжений.

В гидродинамике вводится понятие гидродинамического давления с тем же свойством быть постоянным по всем направлениям в данной точке и в гидростатике;

(3.6)

3.2. Методы Лагранжа и Эйлера

Описание законов движения может быть выполнено по методу Ж.Л. Лагранжа и Л. Эйлера.

Метод Лагранжа предполагает наблюдение за отдельными материальными объектами – частицами жидкости при их перемещении в пространстве. Итог наблюдений за конкретной частицей начальными координатами (рис. 3.2.) при перемещении за время является след , называемый траекторией.

Система функций геометрического характера

(3.7)

описывающих траекторию частиц, позволяет найти кинематические характеристики путем дифференцирования

(3.8)

а также вторые производные – ускорения

(3.9)

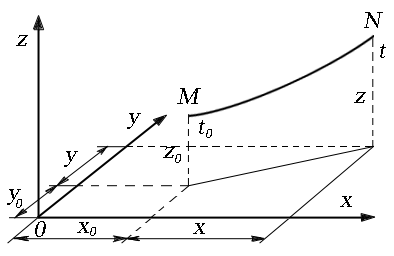
Рис. 3.2. Характер движения жидкости

Метод Эйлера задает поле скоростей в рассматриваемой области движения жидкости. Полное описание задано, если скорости и давления определены в виде

(3.10)

линия, в каждой точке которой в данный момент времени вектор скорости направлен по касательной к ней, называется линией тока. Это основное понятие метода Эйлера. В случае неустановившегося движения в следующий момент движения через ту же точку будет проходить другая линия тока (рис.3.3 а).

Так как вектор с компонентами с элементами с проекциями на оси координат, то из условия параллельности векторов следует пропорциональность их проекций

(3.11)

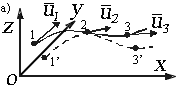
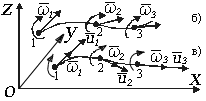
Рис. 3.3. Линия тока и линии завихренности

В случае установившегося движения линия тока сохраняет свое положение в пространстве и совпадает с траекторией.

Каждая частица вращается с угловой скоростью . Линия, во всех точках которой направление векторов совпадает с касательной к ней, является вихревой линией.

Из того, что вектор с компонентами совпадает по направлению с элементом длины вихревой линии , имеющим компоненты , то уравнение вихревой линии имеет вид (рис. 3.3.б)

(3.12)

Линии тока могут совпадать с линиями завихренности. Такое движение называется винтовым и определяется

(3.13)

Совокупность линий тока, проходящих через точки бесконечно малого замкнутого контура , образует элементарную трубку тока (рис. 3.4 а).

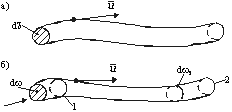
Рис. 3.4. Трубка тока и вихревая трубка

Аналогичное образование в поле угловых скоростей называется вихревой трубкой.

Пучок линий тока, проходящих через все точки площадки , ограниченной контуром называется элементарной струйкой.

Объем жидкости, проходящей через поперечное сечение 1 с площадью за время должен равняться объему жидкости, прошедшему через любое сечение 2 с площадью за то же время в случае несжимаемой среды.