Определение скорости полета снаряда с помощью баллистического крутильного маятника
.docxОпределение скорости полета снаряда с помощью баллистического крутильного маятника
ЗАКОН ИЗМЕНЕНИЯ МОМЕНТА ИМПУЛЬСА И ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Моментом импульса
материальной точки
относительно
некото-рого центра О
называется векторное произведение
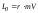 ,
где
,
где
 радиус-вектор
материальной точки, проведенный из
центра О
(рис. 5.1),
радиус-вектор
материальной точки, проведенный из
центра О
(рис. 5.1),
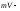 импульс
материальной точки. Величина момента
импульса равна
импульс
материальной точки. Величина момента
импульса равна
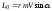 ,
где α
– угол между векторами
,
где α
– угол между векторами
 и
и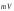 .
.
Проекция вектора
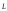 ,
на ось Z
, проходящую через точку 0,
называется моментом
импульса материальной точки относительно
этой оси
,
на ось Z
, проходящую через точку 0,
называется моментом
импульса материальной точки относительно
этой оси
|
Рис. 5.1 |

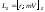 .
Если скорость точки лежит в плоскости,
перпендикулярной оси Z,
то
.
Если скорость точки лежит в плоскости,
перпендикулярной оси Z,
то
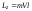 ,
где
,
где
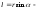 кратчайшее
расстояние от оси вращения до прямой,
вдоль которой направлена скорость.
кратчайшее
расстояние от оси вращения до прямой,
вдоль которой направлена скорость.
Для твердого тела,
вращавшегося вокруг неподвижной оси,
момент импульса определяется выражением
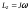 ,
где
J
– момент
инерции тела относительно оси вращения,
ω
– угловая скорость вращения.
,
где
J
– момент
инерции тела относительно оси вращения,
ω
– угловая скорость вращения.
Момент импульса системы тел определяется выражением
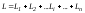 ,
(5.1)
,
(5.1)
где
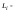 момент импульса i-го
тела. Известно, что производная по
времени от момента импульса механической
системы равна моменту внешних сил,
действующих на эту систему:
момент импульса i-го
тела. Известно, что производная по
времени от момента импульса механической
системы равна моменту внешних сил,
действующих на эту систему:
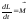 ,
(5.2)
,
(5.2)
где
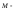 момент
внешних сил. Это утверждение в механике
называют законом
изменения момента импульса (II
законом Ньютона для вращательного
движения). Если система замкнутая, то
момент
внешних сил. Это утверждение в механике
называют законом
изменения момента импульса (II
законом Ньютона для вращательного
движения). Если система замкнутая, то
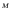 равен нулю, и момент импульса системы
остается постоянным. Это утверждение
называют законом сохранения момента
импульса.
равен нулю, и момент импульса системы
остается постоянным. Это утверждение
называют законом сохранения момента
импульса.
Закон сохранения момента импульса относительно некоторой оси формулируется следующим образом: если момент внешних сил, действующих на систему относительно некоторой оси равен нулю, то момент импульса системы по отношению к той же оси остается постоянным.
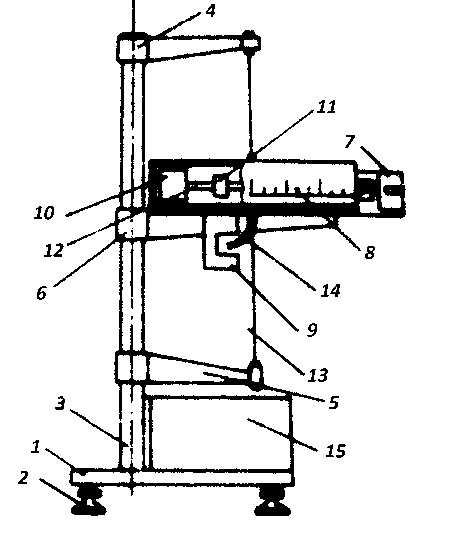
Приборы и принадлежности: баллистический крутильный маятник FРМ-09 или унифилярный подвес с пушкой ФМ 15.
Теория метода и описание прибора
Метод измерения скорости полета снаряда основан на законе сохранения момента импульса относительно некоторой оси.
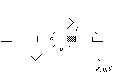
Пусть снаряд массой m, движущийся со скоростью V, попадает в неподвижное уравновешенное твердое тело на расстоянии l от оси вращения и застревает в нем. Применение закона сохранения момента импульса относительно оси вращения дает следующее соотношение
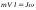 (5.3)
(5.3)
|
Рис. 5.2 |
До столкновения
с телом моментом импульса обладал
лишь снаряд
Зная m, l, J, , можно определить скорость снаряда: |
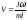 .
(5.4)
.
(5.4)
Сразу после соударения снаряда крутильный маятник обладает только кинетической энергией
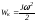 .
(5.5)
.
(5.5)
По достижении максимального отклонения из положения равновесия маятник останавливается, его кинетическая энергия переходит в потенциальную энергию упругой деформации закрученной проволоки
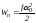 ,
(5.6)
,
(5.6)
где f
– модуль
кручения проволоки; J
– момент инерции маятника вместе со
снарядом;
 наибольшее
значение угловой скорости маятника; 0
– наибольший угол отклонения маятника
из положения равновесия.
наибольшее
значение угловой скорости маятника; 0
– наибольший угол отклонения маятника
из положения равновесия.
Приравнивая выражения (5.5) и (5.6) (по закону сохранения энергии), находим
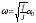 .
(5.7)
.
(5.7)
Тогда выражение (5.4) для скорости снаряда примет вид
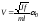 .
(5.8)
.
(5.8)
С другой стороны, движение маятника после попадания в него снаряда описывается основным законом динамки вращательного движения:
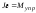 ,
(5.9)
,
(5.9)
где Mупр = – f – момент сил упругости закрученной проволоки.
Так как угловое ускорение ε – вторая производная от угла поворота по времени, то мы приходим к дифференциальному уравнению колебательного движения маятника:
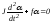 или
или
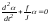 .
(5.10)
.
(5.10)
Это дифференциальное уравнение свободных незатухающих гармонических колебаний. Решением этого уравнения является функция
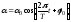 .
(5.11)
.
(5.11)
Выражение (5.11) будет удовлетворять уравнению (5.10) (в чем можно убедиться непосредственной подстановкой) лишь в том случае, когда
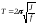 .
(5.12)
.
(5.12)
Подставляя в (5.8) выражение для момента инерции из (5.12), получим
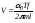 .
(5.13)
.
(5.13)
Специальная методика измерения скорости V позволяет исключить модуль кручения f из формулы (5.13).
Пусть снаряд был выпущен из стреляющего устройства, когда перемещаемые грузы находились на расстоянии R1 от оси вращения. В этом положении момент инерции маятника
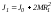 ,
,
следовательно, период колебаний составит
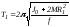 .
(5.14)
.
(5.14)
После перемещения
грузов до расстояния
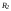 период изменится:
период изменится:
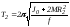 ,
(5.15)
,
(5.15)
где J0 – момент инерции маятника без грузов; M – масса одного груза.
Из соотношений (5.14) и (5.15) можно получить следующее выражение для f:
 .
(5.16)
.
(5.16)
Подставляя выражение
(5.16) в формулу (5.13) для
 с учетом того, что T
= T1,
получим
с учетом того, что T
= T1,
получим
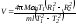 .
(5.17)
.
(5.17)
В формуле (5.17) величины M, m, l – задаются, а величины T1, T2, R1, R2, 0 измеряются.
|
|
|
Рис. 5.3 |
Порядок выполнения работы и обработка результатов
измерений
-
Включить сетевой шнур измерителя в питающую сеть.
-
Нажать переключатель СЕТЬ, проверяя, все ли индикаторы измерителя высвечивают цифру нуль, а также светится ли лампочка фотоэлектрического датчика.
-
Максимально отдалить друг от друга грузы.
-
Установить маятник в таком положении, чтобы черта на мисочке показывала угол отклонения α = 0.
-
Выстрелить снаряд из стреляющего устройства.
-
Измерить максимальный угол отклонения маятника α0.
-
Включить и обнулить счетчик времени.
-
Отклонить маятник на угол α0, включить секундомер и отпустить маятник.
-
Измерить время для двадцати колебаний и вычислить Т1. Пункты 5 – 9 повторить три раза.
-
Максимально приблизить друг к другу грузы М и повторить действия согласно пунктам 4, 7, 8 (исключая пункты 5,6).
-
Измерить время для двадцати колебаний и вычислить Т2. Измерения провести по три раза. Результаты измерений занести в табл. 5.1. Скорость вычислить по формуле (5.17).
Таблица 5.1
|
α0 |
R1 |
t1 |
T1 |
R2 |
t2 |
T2 |
V |
|
|
|
|
|
|
|
|
|
|
α0 cp |
|
|
T1 cp |
|
|
T2 cp |
Vcp |
Контрольные вопросы
-
Сформулируйте цель работы.
-
Как определяется момент импульса материальной точки, твердого тела относительно неподвижной оси вращения?
-
При каких условиях выполняется закон сохранения момента импульса относительно оси?
-
Почему измерения проводятся при двух положениях перемещаемых грузов?
-
Как получить формулу (5.17)?
-
Сделайте выводы по работе.


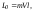 после столкновения
после столкновения
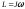 ,
где
,
где
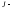 момент
инерции тела вместе со снарядом. По
закону сохранения момента импульса
L0
= L.
момент
инерции тела вместе со снарядом. По
закону сохранения момента импульса
L0
= L.