ЗАНЯТИЕ 1.1 (матем)

МОДУЛЬ 1. ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА, БИОМЕХАНИКА, АКУСТИКА.

ЗАНЯТИЕ 1.1

ТЕМА: «ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА. ПРОИЗВОДНЫЕ.

ИНТЕГРАЛЫ»

Цель занятия: Изучить основы математического анализа, производные первого и высших порядков, определённый и неопределённый интегралы.

Студент должен знать: Методы вычисления производных, основные правила дифференцирования, а так же способы вычисления определённых и неопределённых интегралов, их свойства.

Студент должен уметь: Вычислять, используя основные правила дифференцирования, производные первого и высших порядков, а так же определённые и неопределённые интегралы, используя различные способы интегрирования.

Вопросы, рассматриваемые на занятии:

1.Основные элементарные функции.

2.Понятие производной функции первого порядка. Геометрический и физический смысл производной первого порядка. Основные формулы и правила дифференцирования.

3.Сложная функция и её производная. Основные формулы и правила дифференцирования сложных функций.

4.Производная второго и высших порядков. Физический смысл производной второго порядка.

5.Производная функции нескольких аргументов.

6.Дифференциал функции.

7.Понятие о первообразной функции и неопределённый интеграл.

8.Основные свойства неопределённых интегралов и способы их интегрирования.

9.Определённый интеграл и его свойства. Формула Ньютона-Лейбница.

10.Основные свойства определённых интегралов и способы их интегрирования.

Формулы и закономерности, используемые при решении примеров:

1.Основные элементарные функции

Степенная функция y xn , где x - аргумент, n - натуральное число.

Показательная функция y ax , ( а 0, а 1).

Логарифмическая функция y loga x , где а - основание. Эта функция является обратной показательной функции y ax .

Экспоненциальная функция y ex , где е = 2,718 - основание функции. Эта функция является обратной функции натурального логарифма y ln x

2. Производная функции первого порядка

y/ lim y - производная функции;

xx 0 x

yx/ Vмгн. - мгновенная скорость (физический смысл производной)

некоторой точке (геометрический смысл производной).

Основные формулы и правила дифференцирования

2

2. Сложная функция и её производная:

y f (u) , где u (x) .

yx/ f / (u) ux/

Основные формулы дифференцирования сложных функций

1)(C)/x 0

2)(xx/ ) 1

3)(un )/x nun 1ux/

4)(u )/x ux/ x/ x/

8)(au )/x auux/ ln a

9)(eu )/x euux/

13)(Sinu)/x Cosu ux/

14)(Cosu) /x Sinu u x/

Пример: найти производную сложной функции y Sin3 (ln x) .

Решение: по формулам дифференцирования 3, 13 находим: yx/ 3Sin2 (ln x) Cos(ln x) (ln x)/x 3Sin2 (ln x) Cos(ln x) 1x

3. Производная второго и высших порядков

 yxx// ( yx/ )/x - производная второго порядка

3

4.Производная функции нескольких аргументов.

f (x, y, z...) - функция нескольких аргументов

Пример: найти частные производные функции z 3x2 y 7xy 13x 8 . Решение: zx/ , y const 6xy 7 y 13

zy/ , x const 3x2 y 7x .

5.Дифференциал функции.

dy yx/ dx - дифференциал функции y f (x) ;

dz xz dx yz dy - полный дифференциал функции, зависящей от нескольких аргументов z f (x, y)

Пример: Электрохимический потенциал вычисляется по формуле:

~

0 RT ln C zF ,

где 0 - постоянная растворителя, R – универсальная газовая постоянная, Т – абсолютная температура в Кельвинах, С – концентрация вещества, z – заряд атома, F – число Фарадея, - потенциал электрического поля.

6. Неопределённый интеграл

4

7.Основные свойства неопределённого интеграла:

Производная от неопределённого интеграла равна подынтегральной функции:

( f (x)dx)/x f (x)

Дифференциал от неопределённого интеграла равен подынтегральному выражению:

d f (x)dx f (x)dx

Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С:

dF(x) F(x) C

Постоянный множитель k можно выносить за знак неопределённого интеграла:

kf (x)dx k f (x)dx

Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых:

f1(x) f2 (x) dx f1(x)dx f2 (x)dx

Основные формулы интегрирования.

5

8. Определённый интеграл

двойной подстановки.

9.Основные свойства определённого интеграла:

Определённый интеграл не зависит от обозначения переменной интегрирования:

Определённый интеграл от суммы конечного числа непрерывных функций, заданных на отрезке [a,b] равен сумме определённых интегралов от слагаемых

функций:

Постоянный множитель k можно вынести за знак определённого интеграла:

Если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл сохранит абсолютную величину, но изменит свой знак на

противоположный, т.е.

Если пределы интегрирования равны между собой, т.е. a=b, то определённый интеграл равен нулю.

7

Если подынтегральная функция на отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой точек того же знака, что и функция, т.е. если

Примеры для решения на занятии:

а) найти производные

1. y x4 2x3 ln x ax

2. y 5ax 8 x

3. y ln x

4. y ln(Cosx) Sin2x

5. y ln(eCosx)

8

6. y

Sin3 x

x

7.y ln(ln x)

8.y (x2 3)5 ln x

9.y 2SinxCosx

10.y e x Sinx2

11.y 4x ln x2

12.y ln sin(x2 1)

Найти производные второго порядка:

13.x A sin t, где A, const

14.y 2 ln x / x2

15.y sin 2 x cos 3x

б) Вычислить неопределённые интегралы:

3.e5CosxSinxdx

4.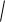(2 x)3 dx

5.CosSinx5 x dx

6.(x2 1)8 xdx

7.ex3 x2dx

xdx

8. 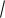a2 x2

9. xdxln x

t2dt

10.(1 2t3 )2

11.ln ax ln b dx

9