
- •II. Медицинская статистика
- •Статистика как общественная наука. Требования, предъявляемые к статистике. Этапы статистического исследования.
- •Развернутый план статистического исследования, основные положения.
- •Статистическое наблюдение. Ошибки статистического наблюдения.
- •Статистическая группировка. Виды группировок. Основные требования к ним. Значение для качественного анализа.
- •Статистическая обработка и сводка материала. Применение вычислительной техники в обработке статистического материала.
- •Виды статистических таблиц и правила их построения.
- •Абсолютные и относительные величины, виды, методы расчета. Возможные ошибки при неправильном применении относительных величин.
- •Виды средних величин. Возможные ошибки при их неправильном применении. Методы расчета средней арифметической простой.
- •Средняя арифметическая взвешенная, понятие, методы расчета.
- •Характеристика разнообразия изучаемого признака, основные показатели, применение в медицине.
- •Методика расчета среднего квадратического отклонения. Сигмальные зоны, их применение в медицине.
- •Коэффициент вариации, методика расчета, градации, значение.
- •Оценка достоверности результатов исследования. Ошибка средней арифметической и относительных показателей.
- •Оценка достоверности результатов исследования. (Доверительные границы средних и относительных величин, их применение в медицине.)
- •Оценка достоверности результатов исследования. Оценка достоверности разности результатов исследования для средних величин и относительных показателей, значение в медицине.
- •Динамические ряды, виды, способы выравнивания. Методика составления анализа динамических рядов.
- •Графическое изображение в статистическом исследовании. Виды графических изображений, правила построения и применения.
- •Предмет и разделы демографии. Значение изучения демографических показателей в практической работе врача.
- •Демография. Источники изучения демографических процессов (учетная документация).
- •Механическое движение населения, социально-гигиеническое значение. Коэффициент механического прироста, его расчет, региональные особенности.
- •Показатели естественного движения населения и их социально-гигиеническое значение.
- •Перепись населения, методика проведения. Основные данные о численности, составе населения в рф и Тюменской области.
- •Коэффициент плодовитости, возрастные показатели, периоды плодовитости, методы расчета, социально-гигиеническое значение.
- •Рождаемость населения, учетная документация, методика расчета и анализа.
- •Естественный прирост населения, методы расчета, социально-гигиеническое значение, региональные особенности.
- •Младенческая смертность как социально-гигиеническая проблема, способы расчета.
- •Младенческая смертность, возрастные и региональные особенности в Тюменской области.
- •Перинатальная смертность, причины, периоды, методика вычисления.
- •Общая и возрастная смертность, причины возрастной смертности населения. Особенности структуры смертности в Тюменской области.
- •Процессы естественного движения населения в районах Крайнего Севера и Западной Сибири.
- •Международная классификация болезней, травм и причин смерти. История создания, принципы построения и пользования. Ее значение для изучения здоровья населения и в работе врача.
- •Источники и основные направления изучения заболеваемости
- •Изучение заболеваемости по данным обращаемости, учетно-отчетная документация.
- •Изучение заболеваемости по данным специального учета, учетно-отчетная документация.
- •Понятие (терминология) и методика вычисления показателей заболеваемости, распространенности и пораженности.
- •Заболеваемость с временной утратой трудоспособности. Инвалидность
-
Оценка достоверности результатов исследования. Оценка достоверности разности результатов исследования для средних величин и относительных показателей, значение в медицине.
Достоверность разности результатов исследования (t) рассчитывается для определения различия между несколькими относительными показателями. При этом решается вопрос, является ли различие показателей существенным (обусловленным действием каких-то факторов) или вызвано случайными колебаниями.
Достоверность разности рассчитывается по формуле:
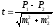
Различия считаются существенными если t = 2 или > 2.
При этом разность соответствует вероятности безошибочного прогноза равной 95,5%.
-
Динамические ряды, виды, способы выравнивания. Методика составления анализа динамических рядов.
Динамический ряд - ряд числовых значений изучаемого признака, показывающих изменения его во времени.
Типы динамических рядов: - Простые
- Сложные (производные)
Простой ряд может быть:
- Моментным
- Интервальным
Методы выравнивания динамического ряда:
-укрупнение интервала
-групповой средней
-скользящей средней
Показатели анализа динамического ряда:
-
Абсолютный прирост - разность между последующим и предыдущим уровнем динамического ряда.
-
Темп прироста - процентное отношение абсолютного прироста к предыдущему уровню динамического ряда. Он показывает скорость изменения явления во времени.
-
Темп роста - процентное отношение последующего уровня динамического ряда к предыдущему. Он показывает на сколько процентов повысился или понизился показатель.
-
Показатель наглядности - процентное отношение последующего уровня динамического ряда к исходному. принятому за основу сравнения. Он дает наглядность о текущем процессе.
Ряд в статистике — это цифровые данные, показывающие, изменение явления во времени или в пространстве и дающие возможность производитьстатистическое сравнение явлений как в процессе их развития во времени,
В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных и производных показателей (относительных и средних величин).
В зависимости от того, как выражают уровни ряда состояние явления на определённые моменты времени (на начало месяца, квартала, года и т.п.) или его величину за определённые интервалы времени (например, за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды динамики.
Способы выравнивания динамического ряда. Способами выравнивания динамического ряда являются: укрупнение периодов, расчет групповой средней, расчет скользящей средней, метод наименьших квадратов
Укрупнение периодов — применяется, когда явление в интервальном ряду выражено в абсолютных величинах, уровни которых суммируются по более крупным периодам. Применение возможно при кратном числе периодов.
Вычисление групповой средней — применяется, когда уровни интервального ряда выражены в абсолютных, средних или относительных величинах, которые суммируются, а затем делятся на число слагаемых. Способ применяется при кратном числе периодов.
Расчет скользящей средней — применяется, когда уровни явлений любого ряда выражены в абсолютных, средних или относительных величинах. Данный метод применяется при наличии некратного числа временных периодов (7, 11, 13, 17, 19) достаточно длинного динамического ряда. Путем вычисления групповой средней значений 3 периодов, а в последующем переходя на определенный уровень и два соседних с ним, осуществляется "скольжение" по периодам. Каждый уровень заменяется на среднюю величину (из данного уровня и двух соседних с ним). Данный метод применяется, когда не требуется особой точности, когда имеется достаточно длинный ряд и можно пренебречь потерей двух значений ряда; в случаях, когда изучается развитие явления под влиянием одного или двух факторов.
Метод наименьших квадратов применяется для более точной количественной оценки динамики изучаемого явления. Этим способом получаются такие выровненные значения уровней ряда, квадраты отклонений которых от истинных (эмпирических) показателей дают наименьшую сумму.
