
- •II. Медицинская статистика
- •Статистика как общественная наука. Требования, предъявляемые к статистике. Этапы статистического исследования.
- •Развернутый план статистического исследования, основные положения.
- •Статистическое наблюдение. Ошибки статистического наблюдения.
- •Статистическая группировка. Виды группировок. Основные требования к ним. Значение для качественного анализа.
- •Статистическая обработка и сводка материала. Применение вычислительной техники в обработке статистического материала.
- •Виды статистических таблиц и правила их построения.
- •Абсолютные и относительные величины, виды, методы расчета. Возможные ошибки при неправильном применении относительных величин.
- •Виды средних величин. Возможные ошибки при их неправильном применении. Методы расчета средней арифметической простой.
- •Средняя арифметическая взвешенная, понятие, методы расчета.
- •Характеристика разнообразия изучаемого признака, основные показатели, применение в медицине.
- •Методика расчета среднего квадратического отклонения. Сигмальные зоны, их применение в медицине.
- •Коэффициент вариации, методика расчета, градации, значение.
- •Оценка достоверности результатов исследования. Ошибка средней арифметической и относительных показателей.
- •Оценка достоверности результатов исследования. (Доверительные границы средних и относительных величин, их применение в медицине.)
- •Оценка достоверности результатов исследования. Оценка достоверности разности результатов исследования для средних величин и относительных показателей, значение в медицине.
- •Динамические ряды, виды, способы выравнивания. Методика составления анализа динамических рядов.
- •Графическое изображение в статистическом исследовании. Виды графических изображений, правила построения и применения.
- •Предмет и разделы демографии. Значение изучения демографических показателей в практической работе врача.
- •Демография. Источники изучения демографических процессов (учетная документация).
- •Механическое движение населения, социально-гигиеническое значение. Коэффициент механического прироста, его расчет, региональные особенности.
- •Показатели естественного движения населения и их социально-гигиеническое значение.
- •Перепись населения, методика проведения. Основные данные о численности, составе населения в рф и Тюменской области.
- •Коэффициент плодовитости, возрастные показатели, периоды плодовитости, методы расчета, социально-гигиеническое значение.
- •Рождаемость населения, учетная документация, методика расчета и анализа.
- •Естественный прирост населения, методы расчета, социально-гигиеническое значение, региональные особенности.
- •Младенческая смертность как социально-гигиеническая проблема, способы расчета.
- •Младенческая смертность, возрастные и региональные особенности в Тюменской области.
- •Перинатальная смертность, причины, периоды, методика вычисления.
- •Общая и возрастная смертность, причины возрастной смертности населения. Особенности структуры смертности в Тюменской области.
- •Процессы естественного движения населения в районах Крайнего Севера и Западной Сибири.
- •Международная классификация болезней, травм и причин смерти. История создания, принципы построения и пользования. Ее значение для изучения здоровья населения и в работе врача.
- •Источники и основные направления изучения заболеваемости
- •Изучение заболеваемости по данным обращаемости, учетно-отчетная документация.
- •Изучение заболеваемости по данным специального учета, учетно-отчетная документация.
- •Понятие (терминология) и методика вычисления показателей заболеваемости, распространенности и пораженности.
- •Заболеваемость с временной утратой трудоспособности. Инвалидность
-
Виды средних величин. Возможные ошибки при их неправильном применении. Методы расчета средней арифметической простой.
Виды средних величин:
-мода
-медиана
-средняя арифметическая
-простая
-взвешенная
Мода-самая частая варианта
Медиана- варианта расположенная посередине ряда
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака (сумма значений признака) в изучаемой совокупности сохраняется неизменным.
Средняя величина - это величина, которая средним цифровым значением характеризует изучаемое явление или признак.
Средняя арифметическая простая= сумма всех числе\количество чисел
Недостатки средних величин заключаются в том, что за ними не видно индивидуальных различий изучаемого явления.
Средние величины рассчитываются из вариационного ряда.
Средняя арифметическая простая рассчитывается из вариационного ряда, в котором каждая варианта встречается один раз. Она рассчитывается по формуле:
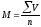
-
Средняя арифметическая взвешенная, понятие, методы расчета.
Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков). Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.
Средняя арифметическая взвешенная высчитывается из вариационного ряда, в котором каждая варианта встречается один раз и более.
Она рассчитывается: - непосредственным способом
- по способу моментов
Средняя арифметическая взвешенная непосредственным способом рассчитывается по формуле:
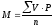
Средняя арифметическая взвешенная по способу моментов рассчитывается по формуле:
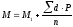
В процессе работы необходимо дать характеристику изучаемого явления (характеристику разнообразия признака). Разнообразие (или похожесть) характеризуют:
- амплитуда
- лимит
- среднеквадратическое отклонение
- коэффициент вариации
-
Характеристика разнообразия изучаемого признака, основные показатели, применение в медицине.
-
Методика расчета среднего квадратического отклонения. Сигмальные зоны, их применение в медицине.
Среднеквадратическое отклонение (сигма) характеризует колеблемость (вариабельность) вариационного ряда и является его абсолютной мерой. Чем большее число наблюдений будет находиться в пределах + одна сигма от средней арифметической, тем однообразнее будет вариационный ряд.
Сигма для средней арифметической, вычисленной по способу моментов, рассчитывается по формуле:
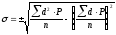
-
Коэффициент вариации, методика расчета, градации, значение.
Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс. В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. Исчисляется в процентах. Вычисляется только для количественных данных.
V=q\x. q- среднее квадратичное отклонение x-средняя величина
Коэффициент вариации характеризует колеблемость (вариабельность) вариационного ряда и является его относительной мерой. Чем меньше показатель, тем однороднее вариационный ряд. Различают степени градации вариации:
низкая (меньше 10,0 %)
средняя (10 - 20,0 %)
высокая ( больше 20,0 %)
