2.3. Достаточные признаки сходимости знакопостоянных рядов.

Признак сравнения.

Пусть даны два знакоположительных ряда (1) и(2). Если для всехвыполняется неравенство, то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).

В качестве рядов для сравнения удобно рассматривать:

–геометрическую прогрессию 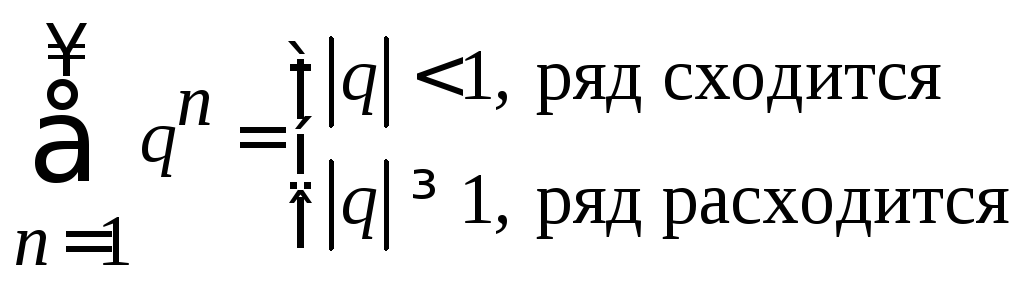– гармонический ряд, который расходится;

– ряд Дирихле ,

Пример 6. Исследовать на сходимость ряд .

Решение

Так как данный n-й член ряда имеет вид ln(1+), где - бесконечно малая величина приn, и известно, что ln(1, то этот ряд сравниваем с рядом

, представляющим собой бесконечно убывающую геометрическую прогрессию со знаменателем q=1/7<1, которая сходится, следовательно, и исходный ряд сходится. ●

Пример 7. Исследовать ряд .

Решение

n-й член данного ряда: ~ , т.е. при n ведет себя как гармонический, следовательно, ряд также расходится. ●

Часто, прежде чем использовать какой-либо из достаточных признаков сходимости ряда, необходимо использовать понятие эквивалентных бесконечно малых величин при и обязательно проверить необходимые условия сходимости исследуемого ряда.

Предельный признак сравнения.

Пусть даны два знакоположительных ряда (1) и(2). Если существует конечный, отличный от 0 предел, то ряды (1) и (2) сходятся или расходятся одновременно.

Пример 8. Исследовать на сходимость ряд .

Решение

Исследуемый ряд .

1. Проверим выполнение необходимого признака

.

2. Ряд с положительными членами.

3. Применим предельный признак сравнения. Для того, чтобы догадаться, с каким рядом целесообразно сравнить данный ряд, рассмотрим его общий член . Для больших значенийn числитель можно считать приближенно равным 2n, a знаменатель - . Поэтому.

Вычислим .

Ряд с общим членом является гармоническим, который всегда расходится, то и данный ряд расходящийся.

Признак Даламбера.

Пусть дан ряд с положительными членами и существует конечный или бесконечный предел. Тогда ряд сходится прии расходится при. Пример 9. Исследовать на сходимость ряд .

Решение

Исследуемый ряд .

1. Необходимый признак выполняется

,

здесь неопределенность , поэтому трижды применяем правило Лопиталя.

2. Ряд с положительными членами.

3. Применим к данному ряду признак Даламбера: ,, вычислим предел отношения

Ряд сходится.

Пример 10. Исследовать на сходимость ряд .

Решение

следовательно, исследуемый ряд сходится.

Пример 11. Исследовать на сходимость ряд

Решение

, следовательно, ряд сходится.

Признак Коши.

Если пристремится к определенному числуq, то при q<1 ряд с положительными членами сходится; приq> он расходится.

Пример 12. Исследовать на сходимость ряд .

Решение

Исследуемый ряд .

1. Необходимый признак выполняется, действительно .

2. Ряд с положительными членами.

3. Общий член ряда находится в n-ой степени, в таких случаях удобно пользоваться признаком Коши

. Ряд сходится.

Пример 13. Исследовать на сходимость ряд .

Решение

, Следовательно, ряд расходится. ●

Интегральный признак Коши.

Если - непрерывная, убывающая, неотрицательная функция для всехи несобственный интегралсходится, то рядсходится, если расходится, то и ряд расходится.

Пример 14. Исследовать на сходимость ряд .

Решение

Исследуемый ряд .

1. Необходимый признак выполняется, действительно .

2. Ряд с положительными членами.

3. Применим интегральный признак. Условия признака выполняются .

. Несобственный интеграл имеет конечное значение, значит, он сходится и сходится исследуемый ряд. ●

Задача 15. Исследовать на сходимость ряд .

Решение

тогда и.

Исследуем несобственный интеграл на сходимость

,

т.е. этот несобственный интеграл сходится, следовательно, и исходный ряд также сходится. ●

В качестве характерных ошибок следует отметить, что иногда сразу пытаются пользоваться каким-либо из достаточных признаков сходимости ряда, не проверив необходимого признака сходимости, например, при исследовании на сходимость ряда:

Задача 16. Исследовать на сходимость ряд

При исследовании этого ряда пытаются сразу применить радикальный признак по которому ряд сходится. Однако,

.

Таким образом, не выполнен необходимый признак сходимости ряда, следовательно, все другие исследования лишены смысла, ряд расходится.