Лекция № 13. Ингибирование роста популяции микроорганизмов продуктами ферментации

Один из наиболее часто встречающихся эффектов, приводящих к отклонению кинетики роста микроорганизмов от экспоненциальной кривой, связан с ингибированием их роста продуктами ферментативных превращений. Накопление какого-либо одного продукта превращения субстрата или их совокуп­ности способно приводить к заметному уменьшению скорости роста культуры, переходу ее в стадию стационарного роста и даже к полной остановке процесса.

В качестве иллюстрации можно указать, что наиболее типичным случаем ингибирования роста микроорганизма продуктами жизнедеятельности является случай накопления в культуре органических кислот, снижающих значение рН среды культивирования. Как известно, скорость ферментативных процессов и, как следствие, скорость роста микроорганизмов рН-чувствительны. Если протоны, взаимодействуя с фун­кционально важными компонентами клетки, блокируют метаболические процессы, феноменологически это означает, что они выступают в качестве ингибиторов роста.

Другим характерным примером могут быть процессы, протекающие с накоплением органических продуктов, в частности спиртов. Как правило, спиртовое брожение останавливается при накоплении в системе определенной концентрации продукта. Эффекты такого рода весьма распространены, в силу этого они требуют тщательного кинетического анализа.

Рассмотрим кинетику роста микробной популяции в приближении, учитывающем кинетически дискриминированные два процесса: стадию взаимодействия субстрата с клеткой и стадию деления клеток.

13.1. Ингибирование продуктом на стадии взаимодействия субстрата с клеткой

Если продукт реакции Р образуется на второй стадии, а процесс ингибирования заключается во взаимодействии продукта с формой N, то кинетическую схему процесса можно представить в виде

(13.1)

Качественно ингибирование процесса продуктом заключается в том, что образуется его комплекс с активной формой N, при этом частица NР теряет способность к осуществлению последующего превращения в X и дальнейшему делению клетки. При развитии процесса с накоплением продукта все большая и большая доля N должна уводиться из реакционноспособного состояния, что должно тормозить процесс роста культуры.

В режиме постоянства концентрации субстрата (S=S₀) переменными во времени компонентами системы являются частицы X, Р и NР. Эти переменные связаны между собой системой дифференциальных уравнений

(13.2)

(13.3)

(13.4)

Сложение этих уравнений с учетом того, что общая биомасса М является суммой концентраций отдельных составляющих, т. е.

(13.5)

приводит к соотношению

(13.6)

Если продукт Р выступает в качестве быстрого и обратимого ингибитора (это означает, что), то процесс образо­вания комплекса активного центра какого-либо фермента с продуктом может быть охарактеризован константой равновесия:

(13.7)

В этом режиме динамика накопления продукта описывается уравнением

(13.8)

где Yр — стехиометрический коэффициент, характеризующий количество продукта на единицу клеточной биомассы.

Из уравнений (13.6) и (13.8) следует весьма важное соотношение

(13.9)

Это означает, что продукт реакции и биомасса связаны между собой простой линейной связью

Yр(Р-Р₀) = (М-М₀) или, если Р₀<<Р, N₀<<М, то Y_рР≈М. (13.10)

Для дальнейшего анализа воспользуемся условиями малости параметра при производной в уравнении (13.3). Если значение константы скорости процесса k₂ достаточно велико, то в уравнении (13.3) можно пренебречь членом (1/k₂)dХ/dτ по сравнению с X. Это приводит к следующему соотношению между переменными:

(13.11)

С учетом (13.11) уравнение (13.5) можно записать в виде

(13.12)

Если учесть, что переменные Р и М связаны линейно по уравнению (13.10), то будем иметь

(13.13)

Подставляя это выражение в (13.6), получим дифференциальное уравнение, описывающее динамику изменения в системе общего количества клеток или общей биомассы:

(13.14)

Уравнение (13.14) может быть записано в форме

, (13.15)

где

(13.16)

Видно, что по своему содержанию уравнение (13.16) соответ­ствует случаю конкурентного ингибирования продуктом. Это уравнение с разделяющимися переменными

(13.17)

которое может быть достаточно просто проинтегрировано:

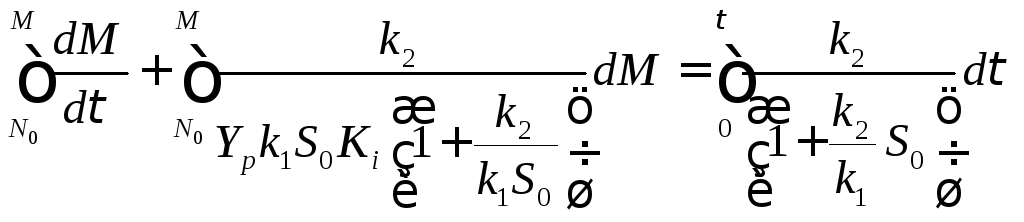(13.18)

или

(13.19)

Если процесс развивается достаточно глубоко, то в уравнении (13.19) можно без особой погрешности пренебречь N₀ по сравнению с М и тогда оно примет вид

(13.20)

Следует обратить внимание на то, что множитель перед τ в правой части уравнения (13.20) представляет собой удельную скорость роста микроорганизма в отсутствие процесса ингибирования продуктом С учетом этого, уравнение (13.20) можно записать так:

(13.21)

Система будет функционировать в двух принципиально различающихся крайних режимах.

1. Если соотношения параметров уравнения (13.21) таковы, что в исследуемом интервале времени

(13.22)

(например, исключительно велика константа ингибирования, (К_i-→∞), то кинетика роста популяции микроорганизма имеет обычный экспоненциальный вид

(13.23)

и процесс ингибирования продуктом никоим образом не отражается на кинетике роста популяции. Эффекты ингибирования пренебрежимо малы.

2. Если соотношения параметров уравнения (13.21) таковы, что имеет место обратное неравенство

(13.24)

(мало значение К_i или k₁S₀), то кинетика роста культуры не описывается экспоненциальной кривой и должно наблюдаться линейное увеличение биомассы:

(13.25)

Для выявления необходимых соотношений между параме­трами, регулирующих направление неравенств (13.22) и (13.24), запишем (13.22) в виде

(13.26)

Поскольку сравнивать функции, указанные в правой и левой частях неравенства, достаточно

неудобно, сравним их производные в точке М = 0, так как неравенство производных в этой точке практически однозначно приводит к неравенству функции при произвольном М. Дифференцирование правой и левой частей неравенства (13.26) по переменной М в точке М = 0 приводит к выражению

(13.27) или

(13.28)

Соотношение (13.28) может быть записано как

(13.29)

С учетом того что в рамках используемой схемы k₂ /k₁ =К_S, неравенство (11.29) будет иметь вид

(13.30)

Из этих неравенств следует, что экспоненциальный или линейный рост микробиологической системы зависит от многих параметров: начальной концентрации клеток, удельной скорости роста, концентрации субстрата. Однако наиболее важным является значение К_i. На качественном уровне можно утверждать, что чем меньше К_i, тем больше значение коэффициента перед линейным членом уравнения (13.21) и тем сильнее проявляются эффекты ингибирования продуктом.

Введем безразмерную переменную M/N₀. Уравнение (13.21) при соизмеримых M и N₀ можно записать в виде

(13.31)

или

(13.32)

где φ=N₀μ/(K_ik₁S₀Y_p). Это уравнение может быть представлено рядом линейных модификаций:

(13.33)

(13.34)

(13.35)

Если механизм процесса сопряжен с ингибированием продуктом реакции, то экспериментально наблюдаемые зависимости должны линеаризоваться в координатах уравнений. Например как следует из уравнения (13.33), должна существовать линейная зависимость экспериментально определяемой величины (1/τ)·ln(M/N₀) от (M/N₀ – 1)/τ. В соответствии с уравнением (13.33) отрезок, отсекаемый этой линейной зависимостью на оси ординат, равен удельной скорости роста; тангенс угла зависимости дает параметр φ.

Величина φ является безразмерным параметром и характеризует эффекты ингибирования продуктом. Если экспериментально найденное значение φ близко к нулю, то можно утверждать, что в исследуемой системе отсутствуют эффекты ингибирования продуктом. Если значение φ в рамках статистической ошибки отлично от нуля, это говорит о заметном вкладе ингибирования продуктом в кинетику роста популяции. Значение константы ингибирования K_i можно определить из уравнения для φ, если известны параметры удельной скорости роста и значение N₀/Y_p.