Лекция №12. Ингибирование роста популяции микроорганизмов избытком субстрата

Одной из характерных особенностей роста микроорганизмов являются часто наблюдаемые эффекты его ингибирования избытком субстрата. Удельная скорость роста культур микроорганизмов на начальном участке зависимости растет с увеличением концентрации субстрата, выходит на «насыщение», а затем при высоких концентрациях субстрата начинает уменьшаться. В силу этого активный рост популяции становится возможным лишь в узком диапазоне концентраций субстрата. Феномены такого рода требуют тщательного анализа и объяснения.

Простейший кинетический механизм, объясняющий эффект ингибирования автокаталитической реакции избытком субстрата, может быть представлен схемой

(12.1)

Если в рамках химико-кинетического приближения записать систему уравнений для каждого из состояний N, X и ХS, концентрация которых изменяется в ходе процесса, то получим систему уравнений при условии, что концентрация субстрата постоянна и равна S₀:

(12.2)

(12.3)

(12.4)

Общее количество биомассы М в системе равно

M=N+X+XS (12.5)

или

(12.6)

Подставив уравнения (12.2) — (12.4) в (12.6), получим

(12.7)

Если процессы на обратимых стадиях схемы (12.1) проте­кают относительно быстро и эти реакции имеют равно­весный характер, то можно выразить связи между пере­менными X, N и ХS с помощью уравнений для констант равновесия

(12.8)

(12.9)

где и — равновесные константы диссоциации комплексов.

В этом случае уравнение (12.5) может быть записано в виде

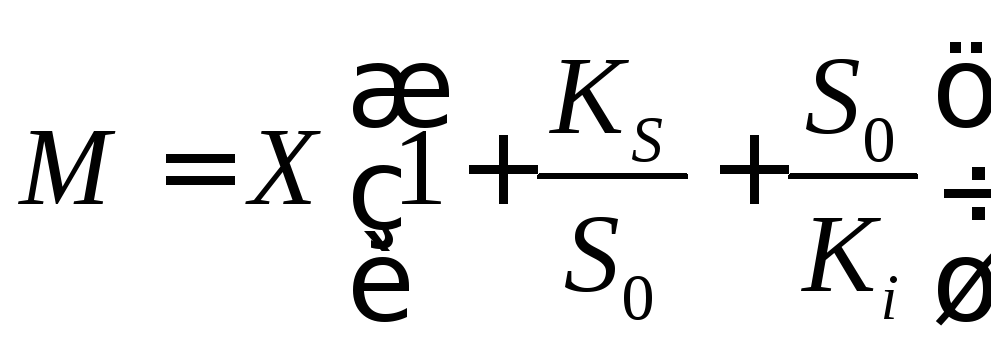(12.10)

или

(12.11)

Подстановка этого соотношения в уравнение (12.7) приводит к дифференциальному уравнению

(12.12)

Решение его при использовании начального условия τ= 0, М = N₀ имеет вид

(12.13)

Общее число клеток экспоненциально увеличивается во времени, при этом удельная скорость роста должна быть представлена уравнением

(12.14)

Из схемы (12.1) следует, что k=μ_m , тогда зависимость удельной скорости роста от концентрации субстрат при ингибировании его избытком запишется

(12.15)

Рассмотрим кинетику процесса до полного исчерпания субстрата. Дифференциальное уравнение роста культуры в условиях ингибирования субстратом имеет вид

(12.16)

где S — текущая концентрация субстрата; K_S и K_i — эффективные значения субстратной константы и константы ингибирования. Это уравнение после разделения переменных можно записать в форме

(12.17)

С учетом балансового соотношения , а также,и приτ=0 N=N₀ интеграл уравнения (12.17) имеет вид

(12.18)

Видно, что отличие этого уравнения от уравнения для процесса в отсутствие ингибирования субстратом заключается в дополни­тельном члене при множителе первого логарифмического слагаемого и в дополнительном отрицательном линейном члене. Из уравнения (12.18) следует, что при К_i→∞ (отсутствие или очень «плохое» ингибирование субстратом) уравнение (12.18) трансформируется в обычное интегральное уравнение роста культуры [см. (11.27)].

Уравнение (12.18) можно преобразовать к виду

(12.19)

Правая часть выражения (12.19) представляет собой удельную скорость роста культуры в экспоненциальной фазе. Действительно, когда величина N близка к N₀(N-N₀≈0), уравнение (12.19) трансформируется к

(12.20)

где

(12.21)

Удельная скорость роста культуры в этом случае является экстремальной функцией концентрации субстрата: при низких концентрациях субстрата скорость роста культуры растет с увеличением его концентрации, при высоких - падает. Для того чтобы выявить ингибирование процесса роста культуры избытком субстрата, в первую очередь необходимо исследовать его динамику в экспоненциальной фазе и показать соответствие экспериментальных данных уравнению (12.21).

Если разложить второй логарифмический член уравнения (12.19) в степенной ряд и использовать первый линейный член разложения, то уравнение (12.19) преобразуется к виду

(12.22)

Если учесть, что, то можно отрицательный член этого уравнения представить в виде

(12.23)

Таким образом, уравнение (12.19) можно записать так:

(12.24)

где

(12.25)

Следовательно, в этом уравнении удалось сгруппировать переменные таким образом, чтобы экспериментальные данные можно было представить в виде линейной анаморфозы, при этом параметры Ф и μ зависят от начальной концентрации субстрата, что позволяет идентифицировать случай развития процесса с ингибированием избытком субстрата.

Параметры μ и Ф могут быть найдены по известной процедуре линеаризации экспериментальных данных в координатах уравнения

(12.26)

Как видно из уравнения (12.25), параметр Ф весьма сложно зависит от начальной концентрации субстрата. Можно выделить три области этой зависимости.

1.

При этом

(12.27)

Параметр Ф не включает в себя константу ингибирования, и, следовательно, ингибирование избытком субстрата не обнаруживается.

2. Здесь проявляется максимальная независимость удельной скорости роста от концентрации субстрата, при этом Ф≈0, а микробная популяция развивается строго экспоненциально вплоть до глубины конверсии 0,6—0,8.

3. В этой области Ф имеет отрицательное значение:

(12.28)

а скорость роста культуры увеличивается по мере израсходования субстрата; накопление продукта реакции и рост клеток опережают экспоненциальный рост.

В общем случае при анализе зависимости Ф от концентрации субстрата можно использовать трансформированное уравнение (12.25)

(12.29)

Необходимо обратить внимание, что

(12.30)

С учетом соотношения (12.30) уравнение (12.29) запишется как

(12.31)

Уравнение (12.31) можно представить следующим образом:

(12.32)

при этом весь пул измерений при росте культур микро­организмов в условиях ингибирования субстратом должен линеаризоваться в координатах зависимости от.Из этой зависимости определяются параметры К_S и K_i .

При анализе экспериментальных данных, если есть основания считать, что процесс может ингибироваться избытком субстрата, можно рекомендовать следующую процедуру. Необходимо исследовать зависимость накопления клеток (или продуктов реакции) в экспоненциальной фазе при различных начальных концентрациях субстрата с определением ц известными и описанными ранее способами. Если зависи­мость обнаружит экстремальный характер, это будет однозначно свидетельствовать в пользу процесса с ин­гибированием избытком субстрата.

Однако информацию о том, что развитие микроорганизма связано с ингибированием избытком субстрата, можно получить и из анализа одной-единственной кинетической кривой роста. Если использовать линеаризацию экспериментальных данных в координатах уравнения (12.26) до степени конверсии 0,4—0,6, то можно определить значения μ и Ф. В том случае, если найденное Ф отрицательно, можно с уверенностью утверждать, что процесс протекает с ингибированием избытком субстрата.