Сложение скоростей

Формулы для аберрации света непосредственно следуют из релятивистского правила сложения скоростей. Пусть система отсчёта S' движется относительно системы отсчёта S со скоростью v вдоль оси x (оси систем параллельны). Если некоторая частица имеет компоненты скорости , в системе S и со штрихами в системе S', тогда выполняются соотношения ^[4]:

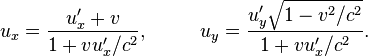
Компоненты скорости частицы, движущейся со скоростью света равны и аналогично со штрихами в системе S'. Подставляя их в преобразования для , получаем формулу для аберрации света. Преобразования для приводят к аналогичной связи для косинусов в обеих системах отсчёта.

2. Релятивистская задержка сигнала;

Рассмотрим движение светового сигнала, излучённого лазерным дальномером, находящимся в пункте i земной поверхности до отражателя s, расположенного на ИСЗ. Используя пространственно-временную метрику Шварцшильда и имея в виду, что для светового сигнала интервал равен нулю, запишем: .

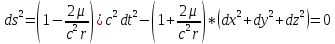Из этого уравнения найдём выражение для скорости распространения светового сигнала в гравитационном поле относительно центра масс Земли. 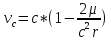Элементарное геодезическое расстояние, пройденное световым сигналом за элементарный промежуток времени, определяется выражением.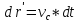, второй член в этом выражении поправочный: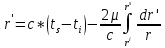. 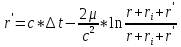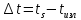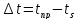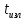Рассматривая движение светового сигнала после отражения от спутникаs обратно к станции i , получим формулу релятивистской задержки(2 её члена): ,, далееЗдесьи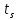моменты излучения сигнала из точкиi и прихода сигнала в точку s по координатному времени, получим 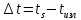Рассматривая движение светового сигнала после отражения от спутникаs обратно к станции i, 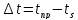Переход от координатного времени к собственному осуществляется с помощью метрики Шварцшильда, поэтому к выражению прибавляется еще один член: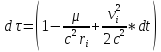

3. Релятивистский доплеровский эффект (смешение частоты).

Пусть имеются трое часов: одни покоящиеся, расположенные в центре масс гравитирующего тела и двое перемещающихся со скоростями 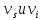. На основании метрики Шварцшильда для связи между промежутками времени по часам в точкахs и О, запишем связь между промежутками времени по часам в точках i и О. 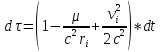. Величина, обратная периоду, называется частотой, тогда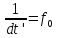– собственная частота,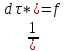- принятая частота. Формула Доплеровского смещения частоты: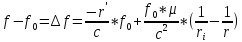+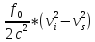. В полученной формуле первый член в правой части называется продольный эффектом К. Доплера, второй член назван наличием гравитационного поля (разностью гравитационных потенциалов в точках i и s), третий член называется поперечным доплеровским эффектом. Смещение частоты сигналов навигационных спутников GPS и ГЛОНАСС, обусловленное влиянием двух последних членов правой части достгает соответственно 0.82 Гц-0.10 Гц.

4. Релятивистская прецессия: а) Схоутена-де Ситтера; б) Прецессия Лензе-Тирринга. Геодезическая прецессия связана с тем, что в теории относительности используется криволинейное риманово пространство. В этом пространстве параллельный перенос не возможен и при полном обороте не вернётся в ту же точку орбиты в виде спирали. Величина не замыкания орбиты и есть геодезическая прецессия.

Прецессия Схоутена-де Ситтера: Прецессия Схоутена – де Ситтера возникает вследствие несовпадения направлений между начальным и конечным положениями вектора при его параллельном переносе по замкнутому контуру в четырѐхмерном криволинейном пространстве. Если считать орбиту Земли круговой и принять еѐ за контур, то в четырѐхмерном пространстве с центрально-симметричной метрикой Шварцшильда угловое несовпадение, в случае параллельного переноса вектора, составит: 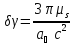*206265, где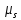– гелиоцентрическая гравитационная постоянная,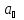- большая полуось орбиты Земли, с – скорость света. Это явление приводит к дополнительному смещению точки весеннего равноденствия на 1.92’’ за столетие и к соответствующему дополнительному вращению эклиптической и экваториальной СК.

Прецессия Лензе-Тирринга.

Прецессия Лензе – Тирринга вызвана вращением притягивающего тела вокруг своей оси. Формулы этой прецессии выводятся из интегрирования релятивистских уравнений движения с учетом компонент метрического тензора, отвечающего за вращение притягивающего тела вокруг своей оси. 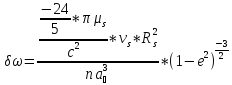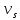В частности, интегрирование уравнений движения Земли приводит к формуле вычисления движения перицентра за один оборот вследствие вращения Солнца: , где е – эксцентриситет земной орбиты, n – среднее движение, Rs – радиус Солнца,– угловая скорость вращения Солнца. Прецессия Лензе – Тирринга приводит к медленному повороту гелиоцентрической системы координат, связанной с перицентром земной орбиты. Перицентр движется при этом в обратном направлении – к точке весеннего равноденствия, в отличие от прямого релятивистского движения перицентра.