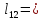20. Преобразования Галилея и Лоренца.

Рис. 4.1. Инерциальные системы координат.

Если в момент времени Ю = 0, начала обеих систем совпали, то преобразование пространственных координат точки Q и времени из одной системы отсчёта в другую для момента времени t задаётся формулами:

Отсюда следует, что ускорения являются инвариантами преобразований Галилея. Инвариантом преобразований Г алилея является и относительная скорость двух материальных точек. Так как вектора ускорения и силы не зависят от системы инерциальных координат, в которых они описаны, то фундаментальный закон природы - второй закон Ньютона инвариантен относительно преобразований Галилея, то есть все механические явления протекают одинаково во всех инерциальных системах отсчёта.

Лоренца: Формулы преобразования координат и времени из одной инерциальной системы отсчёта в другую должны быть такими, чтобы скорость света в двух системах оставалась постоянной величиной. Пусть в какой-либо момент времени t = t' = 0 начала неподвижной oxyz и подвижной систем координат совпали и из начал координат произведена световая

вспышка. Уравнение фронта световой волны в неподвижной системе координат имеет вид

Уравнение (4.4) описывает сферическую поверхность, радиус которой увеличивается со скоростью с. В подвижной системе координат уравнение сферического волнового фронта запишется аналогичным образом

В уравнениях (4.4) и (4.5) скорость света постоянна на основании постулата Эйнштейна. Пусть подвижная система движется в положительном направлении оси абсцисс с постоянной скоростью V относительно неподвижной системы. Выразим координаты точки Q в подвижной системе через координаты неподвижной системы при помощи преобразования Галилея (4.1) и подставим их в уравнение (4.5), получим [6]