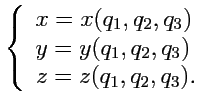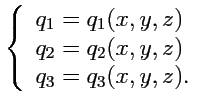- •16. Криволинейные ск. Классификация координат. Понятие о кривизнах.
- •17. Ортогональные криволинейные системы координат. Сферическая ск.
- •19. Элементы теории относительности и её применение в геодезии.
- •20. Преобразования Галилея и Лоренца.
- •21. Пространство Минковского, классификация интервалов, координатное и собственное время.
- •22. Релятивистская шкала времени, её разновидности.
- •23. Связь барицентрического коорд. Времени (tcb) с геоцентрическим коорд. Временем (tcg).
- •Сложение скоростей
16. Криволинейные ск. Классификация координат. Понятие о кривизнах.
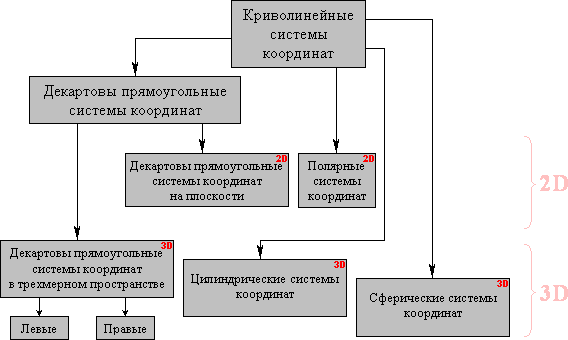
Положение любой точки P в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат. Числа, определяющие положение точки, называются координатами этой точки. Наиболее употребительные координатные системы - декартовы прямоугольные. Кроме прямоугольных систем координат существуют косоугольные системы. Т.к. я не встречал примеров применения косоугольных систем, то я их не рассматриваю. Прямоугольные и косоугольные координатные системы объединяются под названием декартовых систем координат. Иногда на плоскости применяют полярные системы координат, а в пространстве - цилиндрические или сферические системы координат. Обобщением всех перечисленных систем координат являются криволинейные системы координат.
|
|
|
Рис. 1: Классификация систем координат Криволинейные СК |
Говорят,
что в трехмерном пространстве
задана система
координат ![]() ,
если каждой точке M
этого пространства поставлен во взаимно
однозначное соответствие набор чисел
,
если каждой точке M
этого пространства поставлен во взаимно
однозначное соответствие набор чисел ![]() .
(Различным тройкам чисел
.
(Различным тройкам чисел ![]() соответствуют
различные точки пространства). В качестве
таких чисел могут выступать декартовы
координаты, цилиндрические координаты,
сферические координаты и так далее. В
общем случае числа
соответствуют
различные точки пространства). В качестве
таких чисел могут выступать декартовы
координаты, цилиндрические координаты,
сферические координаты и так далее. В
общем случае числа ![]() называются криволинейными
координатами точки
М.
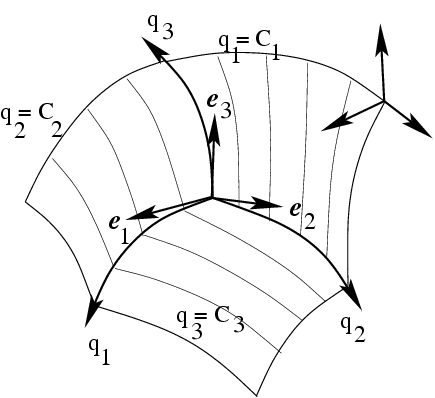
Если координатные линии, проходящие
через любую точку М
пространства, пересекаются под прямым
углом, то система координат называется
ортогональной.
(Напомним, что под углом между линиями
в некоторой точке понимается угол между
касательными к линиям в этой точке). В
частности, декартова, цилиндрическая
и сферическая системы координат являются
ортогональными .
называются криволинейными
координатами точки
М.
Если координатные линии, проходящие
через любую точку М
пространства, пересекаются под прямым
углом, то система координат называется
ортогональной.
(Напомним, что под углом между линиями
в некоторой точке понимается угол между
касательными к линиям в этой точке). В
частности, декартова, цилиндрическая
и сферическая системы координат являются
ортогональными .
![]() Единичный
касательный вектор к координатной
Единичный
касательный вектор к координатной ![]() -линии
в точке М,
направленный в сторону возрастания
координаты
-линии
в точке М,
направленный в сторону возрастания
координаты ![]() ,
называется единичным
ортом
,
называется единичным
ортом ![]() в
точке М.
в
точке М.
![]() Аналогично
определяются единичные орты
Аналогично
определяются единичные орты ![]() и
и ![]() .
.
Как
видно из предыдущего рассмотрения,
определение понятия поля (скалярного,
векторного), основных дифференциальных
операций и характеристик полей было
дано безотносительно к координатной
системе. Однако, при решении конкретных
задач приходится, тем не менее, использовать
систему координат. При этом, в простейшем
случае положение некоторой точки ![]() в
пространстве задавалось с помощью
тройки чисел
в
пространстве задавалось с помощью
тройки чисел![]() так,
что радиус-вектор (бескоординатное
определение положения) представлялся
в виде разложения по неподвижному
декартовому ортонормированному
базису
так,
что радиус-вектор (бескоординатное
определение положения) представлялся
в виде разложения по неподвижному
декартовому ортонормированному
базису![]() ,
,![]() ,
,![]() с
началом в фиксированной точке
с
началом в фиксированной точке![]() в
виде:
в
виде:
![]()
|
|
|
Тройка
чисел ![]() называется
прямоугольными декартовыми координатами
точки
называется
прямоугольными декартовыми координатами
точки![]() .
Использование координат, таким образом,
просто означает способ нумерации точек
пространства и декартовая система
координат в этом смысле не является
уникальной. Кроме того, несмотря на свою
простоту, эта система может сильно
затруднить решение некоторых задач,
требующих использования координатных
систем. Поэтому во многих случаях бывает
удобно определять положение точки в
пространстве не числами
.
Использование координат, таким образом,
просто означает способ нумерации точек
пространства и декартовая система
координат в этом смысле не является
уникальной. Кроме того, несмотря на свою
простоту, эта система может сильно
затруднить решение некоторых задач,
требующих использования координатных
систем. Поэтому во многих случаях бывает
удобно определять положение точки в
пространстве не числами![]() ,
а какими-нибудь другими
,
а какими-нибудь другими![]() .
.
Числа ![]() называютсякриволинейными
координатами точки.
Тогда, радиус-вектор точки
называютсякриволинейными
координатами точки.
Тогда, радиус-вектор точки ![]() должен
быть, как и в случае декартовой системы
координат, функцией криволинейных
координат, т. е.
должен
быть, как и в случае декартовой системы
координат, функцией криволинейных
координат, т. е.![]() или
в проекциях на декартовые оси координат
или
в проекциях на декартовые оси координат
|
|
(184) |
С
другой стороны, задание тройки ![]() также
определяет положение точки в пространстве,
поэтому ее криволинейные координаты
должны быть функциями декартовых:
также
определяет положение точки в пространстве,
поэтому ее криволинейные координаты
должны быть функциями декартовых:
|
|
Таким
образом, положение точки в пространстве
можно определить относительно семейства
поверхностей, на каждой из которых
соответствующая координата имеет
постоянное значение. Поэтому, такие
поверхности называются координатными.
Попарные пересечения координатных
поверхностей ![]() ,
, ![]() ,
, ![]() определяют
пространственные кривые, вдоль которых
изменяется только одна из
координат,
определяют
пространственные кривые, вдоль которых
изменяется только одна из
координат, ![]() ,
, ![]() или
или ![]() .
Такие линии называются координатными
линиями.
Так как уравнения в общем случае не
обязательно задают плоскости, то
и координатные
линии также будут кривыми,
что и определяет название криволинейная
система координат.
.
Такие линии называются координатными
линиями.
Так как уравнения в общем случае не
обязательно задают плоскости, то
и координатные
линии также будут кривыми,
что и определяет название криволинейная
система координат.