
КОМПЛЕКСНЫЕ ЧИСЛА2015
.pdfКОМПЛЕКСНЫЕ ЧИСЛА
Построение системы комплексных чисел
Комплексные числа вводятся в связи со следующей задачей. Известно, что действительных чисел недостаточно для того, чтобы решить любое квадратное уравнение с действительными коэффициентами. В частности, в R не имеет решений уравнение x2 1 0. Это обстоятельство стимулировало необходимость расширения системы действительных чисел R до такой системы чисел, в которой это уравнение уже обладало бы корнем. С другой стороны, определенные на множестве R операции сложения и умножения обладают «хорошими» свойствами. На прошлой лекции мы поняли, что группоид является группой, а группоид полугруппой с единицей.
Хотелось бы, чтобы операции, определенные в новой системе чисел, обладали бы аналогичными свойствами.
Таким образом, задача, стоящая перед нами такова: построить такое новое множество чисел, чтобы
1.в новой системе уравнение x2 1 0 имело бы корень,
2.множество R являлось бы подмножеством нового множества,
3.операции сложения и умножения, определенные на новом множестве, обладали бы всеми основными свойствами, какими обладают операции в системе действительных чисел (обе они ассоциативны и коммутативны, связаны законами дистрибутивности и для них существуют обратные операции – вычитание и деление, кроме деления на нуль.).
Оказывается, что множество чисел С= a bi | a,b R операции сложения и умножения в котором определяются так, как указано ниже, удовлетворяет всем вышеперечисленным свойствам. Здесь i – некоторый
символ, не принадлежащий R такой, что i2 1. Доказательство существования поля комплексных чисел можно найти в учебном пособии «Алгебра и теория чисел» Мартынова Л.М.
Алгебраическая форма комплексного числа. Действия над комплексными числами в алгебраической форме.
Таким образом, под комплексным числом будем понимать формальное выражение вида a+bi. При этом число a называется действительной частью, а b – мнимой частью этого комплексного числа. Букву i называют
мнимой единицей.

Представление комплексных чисел в виде z a bi называется
алгебраической формой комплексного числа. Действительную часть a
числа z будем обозначать через Re z , а мнимую часть b числа z – через Im z . Число z a bi называется сопряженным к z . Если b 0 , то число z называется мнимым, а если, кроме того, a 0 , то число z называется чисто мнимым. Комплексные числа вида a 0i являются действительными числами.
Два комплексных числа считаются равными тогда и только тогда, когда равны их действительные и мнимые части, т.е.
a bi c di a c b d . |
(1) |
Определим на множестве С две бинарные алгебраические операции сложения и умножения следующими равенствами:
(a bi) (c di) (a c) (b d)i , |
(2) |
(a bi) (c di) (ac bd) (ad bc)i . |
(3) |
Обратите внимание на то, что знак «+» в выражении |
a bi является просто |
символом и пока не несет никакой смысловой нагрузки, в то время как при расположении его между действительными или комплексными числами он означает соответствующую операцию сложения.
Если даны два комплексных числа z a bi и u c di , где z 0 , то, в С существует частное, которое можно вычислить по формулам (4) и (3):
u |
uz 1 |
ac bd |
|
ad bc |
i . |
(5) |
|
a2 b2 |
|
||||
z |
|
|
a2 b2 |
|
||
! Формулы (3) и (5) не надо запоминать. Все алгебраические операции над комплексными числами, записанными в алгебраической форме, можно осуществлять как над обычными двучленами, учитывая лишь, что i2 1.
Пример.
а) Вычислить (2 i)2 . (2 i)2 4 4i i2 4
23 i
б) Вычислить 3 i .
23 i (23 i) (3 i) 3 i (3 i) (3 i)
4i 1 3 4i .
(69 1) ( 23 3)i |
|
70 20i |
7 2i . |
|
9 1 |
9 1 |
|||
|
|
Умножили числитель и знаменатель дроби на число, сопряженное знаменателю.

Свойства сопряженных комплексных чисел.
Для любых комплексных чисел z a bi и |
w c di справедливы |
следующие свойства: |
|
1)z w z w , т.е. сопряженное к сумме равно сумме сопряженных;
2)z w z w , т.е. сопряженное к произведению равно произведению сопряженных;
3)z z R, т.е. сумма комплексного числа и его сопряженного есть действительное число;
4)z z R, т.е. произведения комплексного числа на сопряженное есть действительное число;
5)z z z R, т.е. сопряженное к комплексному числу совпадает с этим числом тогда и только тогда, когда оно является действительным числом.
Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числа.
Действительные числа геометрически изображаются точками числовой прямой. Комплексное число a+bi можно рассматривать как пару действительных чисел (a;b) . Поэтому естественно комплексные числа
изображать точками плоскости. Пусть на плоскости задана прямоугольная система координат. Комплексное число z a bi изображается точкой плоскости с координатами (a;b) ; эту точку условимся обозначать той же
буквой z (рис.1).
Y
bi |
|
|
z |
α |
|
|
|
|
|
|
|
|
|
|
|
0 |
a |
X |
|
Такое соответствие между комплексными числами и точками плоскости взаимно-однозначно: каждому комплексному числу z=a+bi соответствует одна точка плоскости с координатами (a;b) и, наоборот, каждой точке
плоскости с координатами (a;b) соответствует одно комплексное число
z=а+bi. Поэтому слова «комплексное число» и «точка плоскости» часто употребляются как синонимы. Плоскость, на которой изображаются комплексные числа, называют комплексной.

При такой интерпретации действительные числа а, т.е. комплексные числа вида a+0i, изображаются точками с координатами (a; ) , т.е. точками
оси абсцисс. Поэтому ось абсцисс называют действительной осью. Чисто мнимые числа 0+bi изображаются точками с координатами ( ;b) , т.е.
точками оси ординат, вследствие этого ось ординат называют мнимой осью. Можно также считать, что комплексному числу z=a+bi соответствует
вектор с координатами (a;b) . Тогда, например, можно находить сумму комплексных чисел по правилу параллелограмма сложения векторов.
Сопряженные комплексные числа z и z a bi симметричны относительно действительной оси.
Определение 1. Модулем комплексного числа z a bi называется длина соответствующего этому числу вектора.
Обозначение:. | z |
Понятно, что | z | 
 a2 b2 .
a2 b2 .
! Модуль комплексного числа совпадает с абсолютной величиной числа только для действительных чисел.
Геометрически очевидно, что комплексное число z 0 будет задано, если помимо модуля указать еще и направление вектора, задав, например величину угла .
Y
bi |
|
|
z |
α |
|
|
|
|
|
|
|
|
|
|
|
0 |
a |
X |
|
Определение 2. Аргументом комплексного числа z 0 называется величина угла между положительным направлением действительной оси и вектором z .
Обозначение: arg z =α.
Замечание. 1) Аргументов комплексного числа z 0 бесконечно много, все они являются. Все они отличаются на величину, кратную 2 .
2) Заданием | z | и arg z комплексное число z 0
определяются однозначно.
3) Для числа z 0 аргумент не определяется.
Действительная и мнимая части комплексного числа z a bi выражаются через его модуль z = r и аргумент следующим образом
a r cosα , b r sin α .
Таким образом, аргумент комплексного числа может быть найден из системы
cos |
|
|
|
|
a |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a2 b2 |
||||||||
|
|
|
|
a |
|
|
|
|
|
||
sin |
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
||||
|
a |
2 |
b |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
Тригонометрическая форма комплексного числа
Каждое комплексное число z a bi , z 0 , может быть записано в виде
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|||
Z |
a2 b2 |
|
|
|
|
|
|
r(cos i sin ) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a |
2 |
b |
2 |
|
|
a |
2 |
b |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z r(cos i sin ) |
, где r R . |
(1) |
||||
Это так называемая тригонометрическая форма комплексного числа
z .
Представление комплексного числа в тригонометрической форме однозначно с точностью до углов, кратных π .
Значение аргумента, которое находится в промежутке от 0 до 2 , будем называть главным значением аргумента и обозначать через Arg z . Легко
понять, что любое комплексное число z 0 можно однозначно представить в тригонометрической форме
z | z | (cosα isin α) , |
(1 ) |
где = Arg z .

Правило нахождения главного значения аргумента:
0)находим главное значение arctg ba β ; это угол в I четверти;
1)если точка z лежит в I четверти, то α Arg z β ;
2)если точка z лежит во II четверти, то α Arg z π β ;
3)если точка z лежит в III четверти, то α Arg z π β ;
если точка z лежит в IV четверти, то α Arg z π β .
Пример. Представить в тригонометрической форме комплексные числа:
а) z 1 
 3i ; б) u 1 i ; в) v
3i ; б) u 1 i ; в) v 
 3 i .
3 i .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
( 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
а) |
| z | |
|
|
( |
3)2 |
|
|
4 2, |
arctg |
|
|
|
arctg |
|
3 |
. Так как точка |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||
z |
лежит |
|
во |
|
II |
четверти, |
|
|
то |
согласно |
|
|
правилу |
2) |
|
|
α Arg z π β |
|||||||||||||||||||||||||||||||||||||
|
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 2 |
|
|
|
|
|
i sin |
|
||||||||||||||||||||
= |
|
|
|
. |
|
|
|
Таким |
|
|
образом, |
|
|
cos |
|
|
|
|
|
– |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|||||
тригонометрическая форма числа z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg1 |
π |
. |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
| u | |
|
|
( 1)2 ( 1)2 |
|
|
|
|
|
|
β arctg |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
б) |
|
|
2 , |
|
|
Так как точка u |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
лежит во II |
четверти, то согласно правилу 3) |
α Arg z π β = π |
π |
π . |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 i |
|
|
|
|
|
|
|
|
5 |
i sin |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Таким образом, |
|
2 cos |
|
|
|
|
– тригонометрическая форма |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
числа u . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
в) | v | |
|
|
( |
|
|
3)2 ( 1)2 |
|
4 2 , |
arctg |
arctg |
|
|
|
|
. Так как точка |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
v |
лежит |
|
в |
|
|
IV |
четверти, |
|
то |
|
согласно |
правилу |
4) |
|
|
|
α Arg z π β = |
|||||||||||||||||||||||||||||||||||||
|
π |
|
π |
|
|
|
|
|
π |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= π |
|
|
|
. |
Таким |
образом, |
i cos |
|
|
|
|
|
|
|
|
|
|||
тригонометрическая форма числа v.
i sin |
π |
– |
|
|
|
||
|
|
|
|

Действия над комплексными числами в тригонометрической форме
С помощью тригонометрической формы можно легко выполнять умножение и деление комплексных чисел, возведение их в степень и извлечение корня любой степени.
1. Умножение и деление.
Теорема. Модуль произведения двух комплексных чисел равен произведению их модулей, т.е.
|
z w |
|
|
|
z |
|
|
|
w |
|
; |
(1) |
|
|
|
|
|
|
|||||||
аргумент произведения равен сумме аргументов сомножителей, т.е. |
|
|||||||||||
arg(z w) arg z arg w . |
(2) |
|||||||||||
Другими словами, при умножении комплексных чисел их модули
перемножаются, а аргументы складываются.
Теорема Модуль частного комплексных чисел равен частному их модулей, т.е.
z |
|
|
| z | |
; |
(3) |
|
w |
| w | |
|||||
|
|
|
|
аргумент частного равен разности аргументов, т.е.
|
z |
|
|
|
|
arg |
|
arg z arg w . |
(4) |
||
|
|||||
w |
|
|
|||
Другими словами, при делении комплексных чисел их модули делятся,
а аргументы вычитаются.
2. Возведение в степень.
Для умножения комплексных чисел следует перемножить их модули и сложить аргументы. Ясно, что это правило остается в силе и для любого конечного числа сомножителей. Следовательно, для любого комплексного

числа z r(cosα isin α) и любого натурального числа n модуль z n |
будет |
||
равен r n , а аргументом zn будет nα , т.е. справедлива формула |
|
||
|
r(cos i sin ) n rn (cos n i sin n ) |
, |
(5) |
которая называется формулой Муавра. |
|
||
Полученная формула верна и для отрицательных целых чисел n. |
|
||
Теорема Для любого целого числа n и любого комплексного числа
z r(cosα isin α) справедлива формула Муавра (5). |
|
r(cosα i sin α) n r n (cosnα i sin nα), |
(5) |
Пример. Вычислить (1 i
 3)6 .
3)6 .
Имеем 1 i 
 3 2(cos 3 i sin 3 ) . Применим формулу Муавра: (1 i
3 2(cos 3 i sin 3 ) . Применим формулу Муавра: (1 i
 3)6
3)6
= 26 (cos2 i sin 2 ) 26 64.
4. Извлечение корня.
Теорема. Для любого натурального числа n |
корень n -й степени из |
||||||||||||
любого ненулевого |
комплексного числа |
z r(cosα isin α) существует и |
|||||||||||
имеет n различных значений, которые находятся по формуле |
|
|
|||||||||||
|
|
|
|
|
|
|
|
α πk |
|
α πk |
|
||
|
|
|
|
|
|
|
|
||||||
wk n z n |
r(cosα i sin β) n r cos |
|
i sin |
|
, |
( 8 ) |
|||||||
n |
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
k , , , ...,n .
Учитывая, что модули всех корней одинаковы и равны n r , а аргументы отличаются на слагаемые, кратные nπ , легко дать им геометрическую
r , а аргументы отличаются на слагаемые, кратные nπ , легко дать им геометрическую
интерпретацию: все корни n -й степени из данного ненулевого комплексного
числа расположены на окружности радиуса n r с центром в начале координат и делят эту окружность на n равных частей (т.е. находятся в вершинах правильного n-угольника, вписанного в эту окружность).
r с центром в начале координат и делят эту окружность на n равных частей (т.е. находятся в вершинах правильного n-угольника, вписанного в эту окружность).
Пример. Вычислить 3 i .
i .
Имеем |
i cos |
3 |
i sin |
3 |
. По формуле ( 8 ) получаем, что |
|
|
|||||||||
2 |
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
wk |
|
|
|
π / πk |
i sin |
π / πk |
k |
π i sin |
k |
π , |
||||||
|
||||||||||||||||
|
cos |
|
|
|
|
= cos |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k , , .

Отсюда
w cos |
π |
i sin |
π |
i , |
w cos π |
i sin π |
|
|
, |
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||||
|
|
w cos π |
i sin π |
|
|
. |
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. Корни n-й степени из единицы. Поскольку (cos isin ) , из формулы (8 ) получаем, что все корни n-й степени из 1 имеют вид
e n |
|
cos |
2 k |
i sin |
2 k |
, k 0,1, 2, ..., n 1 |
(9) |
|
1 |
||||||||
|
|
|||||||
k |
|
|
n |
|
n |
|
||
|
|
|
|
|
||||
Действительные значения корня n-й степени из 1 получаются из формулы
(9) при значениях k 0 и |
n |
, если |
n – четное число, и только при k 0 , если |
|
2 |
||||
|
|
|
||
n – нечетное число. |
|
|
|
На комплексной плоскости корни n-й степени из 1 расположены на окружности единичного радиуса с центром в начале координат и делят эту окружность на n равных частей. Понятно, что одной из точек деления служит число 1. Отсюда следует, что те корни, которые не являются действительными, расположены симметрично относительно действительной оси, т.е. попарно сопряжены.
Пример. Вычислить 4 1 .
1 .
По формуле (9) имеем
e 4 |
|
|
cos |
2 k |
i sin |
2 k |
cos |
k |
i sin |
k |
, k 0,1,2,3. |
|||||||||
|
1 |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||
k |
4 |
|
|
4 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Придавая значения k 0,1,2,3 , получаем |
|
|
|
|
|
|
|
|
|
|||||||||||
e cos0 isin 0 1, |
e cos |
i sin i , |
|
|
|
|
|
|||||||||||||
0 |
|
|
|
|
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
e2 cos isin 1, |
|||||||||
|
|
|
|
Y |
|
|
|
|
|
e |
cos |
3 |
|
i sin |
3 |
i .Таким |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
3 |
2 |
2 |
|
||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
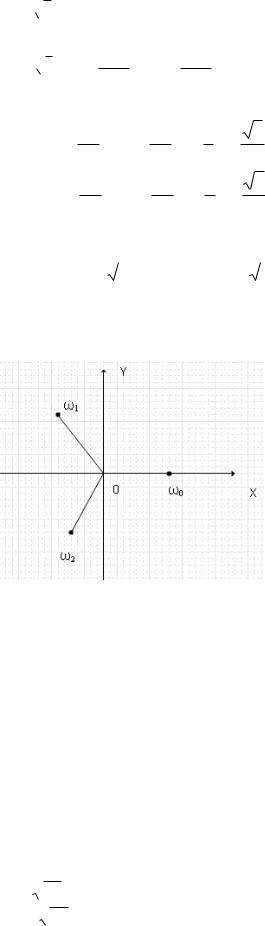
образом, 4 1 {1, 1,i, i} |
|||||||||
|
-1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
O |
|
|
|
X |
|
|
|
|
|
|
|
|
|
||
-i
Пример. Вычислить 3 1 . По формуле (9) имеем
1 . По формуле (9) имеем
ek 3 1 cos 23k i sin 23k , k 0,1, 2 . Отсюда e0 cos0 isin 0 1,
1 cos 23k i sin 23k , k 0,1, 2 . Отсюда e0 cos0 isin 0 1,
e1 cos 23 i sin 23 12 i 23 , e2 cos 43 i sin 43 12 i 23 .
Таким образом,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e 1, |
e |
1 |
i |
3 |
, |
e |
1 |
i |
3 |
|
|||
0 |
1 |
2 |
|
2 |
|
2 |
2 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
||||||
кубические корни из 1.
Значение корней n-й степени из 1 подчеркивает следующая
Теорема Все корни n-й степени из комплексного числа z можно получить умножением одного из них w на все корни n-й степени из 1.
Пусть e0 ,e1,...,en 1 – корни n-й степени из 1. Рассмотрим комплексные числа
w0 we0 , w1 we1,...,wn 1 wen 1 . |
|
|
|
(10) |
Каждое из этих чисел является корнем n-й степени из z |
( wn |
= |
(we |
)n |
|
i |
|
i |
|
= wnein z 1 z ), их n и все они попарно различны. Следовательно, в (10) содержатся все корни n-й степени из z .
Пример. Вычислить 4 16 .
16 .
Одним из значений 4 16 является число w 2 . Учитывая теорему 5 и пример 3, заключаем, что 2, 2,2i, 2i – все корни 4-й степени из числа 16.
16 является число w 2 . Учитывая теорему 5 и пример 3, заключаем, что 2, 2,2i, 2i – все корни 4-й степени из числа 16.
