Комплексные числа шпаргалка
.pdf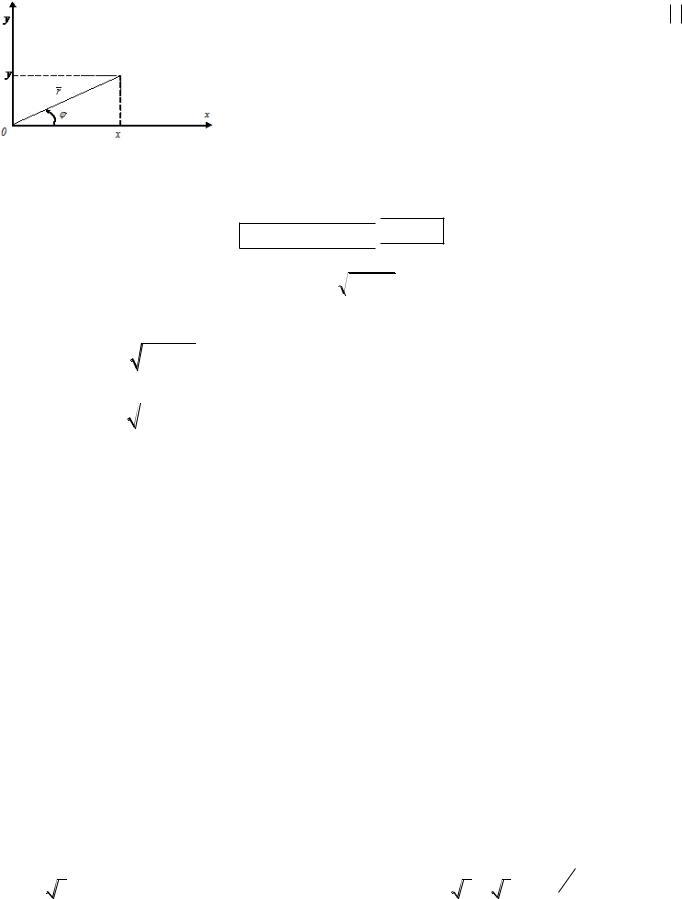
Комплексные числа
Комплексное число z = x + iy изображается в плоскости ХОУ точкой М с координатами (х, у) или вектором с координатами (х, у).
Длина r вектора z называется модулем числа z и обозначается z .
Угол между положительным направлением оси ОХ и вектором z называют аргументом комплексного числа и обозначают Arg z.
Он определяется с точностью до слагаемого, кратного 2 . Значение arg z аргумента z, удовлетворяющее условию 0 arg z 2 или
arg z называется главным. |
|
Имеем Arg z arg z 2k , |
k 0, 1, 2,... |
Тригонометрическая и показательная форма комплексного числа
z r cos i sin 
z rei
Чтобы перейти от алгебраической формы комплексного числа к тригонометрической (показательной) нужно:
1.Найти модуль к.ч. z = x + iy по формуле r 
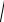x2 y2 .
2.Изобразить к.ч. z = x + iy на комплексной плоскости и определить аргумент из системы:
|
|
|
|
|
x |
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
2 |
y |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
y |
|
|
|
|
|
||
sin |
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
x2 y2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Действия над комплексными числами в тригонометрической и показательной форме
1. |
Умножение и деление. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
z r |
cos i sin |
; |
|
z |
r cos |
2 |
i sin |
2 |
; |
|
|
z |
r ei 1 , z |
2 |
r ei 2 |
|||||||||||||||||||||||||||||
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
2 |
2 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
r r e |
i( 1 2 ) |
|
||||||
|
|
z |
z |
2 |
r r |
cos |
|
2 |
i sin |
2 |
; |
|
|
|
|
|
|
|
z |
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
1 2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 2 |
|
|
|
||||||||||||
|
|
z1 |
|
|
r1 |
cos |
|
2 |
i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
|
|
r1 |
|
|
i( 1 2 ) |
|
|||||||||||||||
|
|
z2 |
|
|
|
r2 |
1 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
z |
|
r |
e |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2. Возведение в целую степень. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
z r cos i sin ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z rei |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
zn |
|
rn cos n i sin n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
n |
r |
n |
e |
in |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. |
Извлечение корня. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
z r cos i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z rei |
|
|
|
|
|
|
|
||||||||||||||||||||
|
Для любого натурального числа n корень n - й степени из любого ненулевого комплексного числа |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
z r cos i sin ( z rei ) существует и имеет n различных значений, которые находятся по |
||||||||||||||||||||||||||||||||||||||||||||
|
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k |
||||||||||||
wk n r |
|
|
|
|
i sin |
|
|
0,1, 2, ..., n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
cos |
|
|
|
|
|
|
, k |
|
n z n re |
|
|
|
|
|
n , k 0, 1, 2, ..., n 1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||