
- •Введение
- •1. ИЗГИБ ПРЯМОУГОЛЬНОЙ ГИБКОЙ ПЛАСТИНЫ
- •1.1. Деформации
- •1.2. Уравнения равновесия
- •1.3. Физические уравнения
- •1.4. Система разрешающих уравнений
- •1.5. Граничные условия
- •1.6. Метод последовательных приближений
- •1.7. Пример 1
- •1.8. Пример 2
- •2. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ РАМЫ
- •2.1. Постановка задачи
- •2.2. Пример 1
- •2.3. Пример 2
- •2.4. Пример 3
- •Список рекомендуемой литературы

|
2w |
|
Nx w |
|
2w |
|
Ny w |
||||||
Nx |
|
|
|
|
|
Ny |
|
|
|
|
|
|
dxdy |
x2 |
x x |
|
2 |
|
|
||||||||
|
|
|
y |
|
y |
|
y |
||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
исдвигающих сил:
S wdx (S Sdy)( w 2w dy)dx
x y x x y
S wdy (S Sdx)( w 2w dx)dy
|
y |
|
|
|
x |
|
y |
|
x y |
||||
|
2w |
|
S w |
|
|
2w |
|
S w |
|||||
S |
|
|
|
|
|
S |
|
|
|
|
|
|
dxdy . |
x y |
y x |
x y |
|
|
|||||||||
|
|
|
|
x y |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теперь сложим эти три суммы, исключив из них подчеркнутые слагаемые согласно равенствам (13) и (14), и добавим внешнюю на-
грузку q. После преобразований получим уравнение равновесия: |
|
||||||||||||||||||||||||||||||||||||||
|
|
Q |
|
|
|
|
Qy |
|
|
|
2w |
|
|
|
|
|
|
|
2w |
|
И |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x |
|
|
|
|
|
|
Nx |
|
|
2S |
|
|
|
|
|
|
|
Ny |
|
|
q. |
|
|
(15) |
|||||||||||
|
|
x |
|
|
y |
|
|
|
x2 |
|
|
|
|
|
x y |
|
|
|
y2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|||||
|
Уравнения равновесия, связывающие изгибающие, крутящие |
||||||||||||||||||||||||||||||||||||||
моменты и поперечные силы, имеют вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
M |
|
|
|
|
H |
|
|
|
H |
А |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
Qx ; |
|
|
|
|
|
|
|
|
|
|
|
Qy |
. |
|
|
|
|
|
|
|
|
(16) |
|||||
|
|
x |
|
|
|
|
y |
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Подставим формулы (16) для поперечных сил Qx , Qy в уравне- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ние (15), которое примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2M |
x |
|
|
2 |
2H |
|
2My |
N |
x |
|
2w |
2S |
|
2w |
N |
y |
2w |
q . |
(17) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|||||
|
x |
|
|
|
|
|
|
x y |
|
|
б2 |
|
|
|
|
|
x y |
|
|
|
y |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3. Физические уравнения |
|
|
|
|
|
|
|
|||||||||||||||||
|
СогласноСзакону Гука деформации срединной поверхности оп- |
||||||||||||||||||||||||||||||||||||||
ределяем по внутренним усилиям: |
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|||||||||||||||||||||||
|
|
x0 |
|
1 |
Nx Ny ; |
y0 |
|
|
|
1 |
Ny Nx ; 0 |
. |
|
(18) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
G |
|
|
|
|||||||||
Изгибающие моменты определяем по функции прогибов:
|
|
|
2w |
|
2w |
|
|
|
2w |
|
2w |
|
||||||||
M |
x |
D |
|
|
|
|
|
|
|
; M |
y |
D |
|
|
|
|
|
|
; |
|
|
2 |
|
|
2 |
|
2 |
|
2 |
||||||||||||
|
|
x |
|
y |
|
|
|
y |
|
x |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
H (1 )D |
2w |
. |
|
|
|
|
|
|
|
|
(19) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|||
7
1.4. Система разрешающих уравнений
Подставим деформации (18) в левую часть равенства (10) и моменты (19) в (17). В результате получим систему из двух уравнений относительно четырех неизвестных функций: Nx , Ny , S и w. Если
теперь усилия Nx , Ny , S выразить через функцию напряжений
Nx |
2 |
, |
Ny |
2 |
, |
S |
2 |
, |
(20) |
y2 |
x2 |
x y |
где , то получим систему из двух нелинейных дифференциальных уравнений в частных производных относительно двух неизвестных функций w и :
|
|
|
|
|
|
|
|
|
|
|
2w 2 |
|
|
И |
|
|
|
|
|||||||||||||
|
|
1 4 |
|
|
|
|
|
2w |
2w |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 0; |
|
|
|||||||
|
|
E |
|
|
|
|
|
|
|
x |
|
y |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 2w |
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
||||||||||||
4 |
|
|
|
|
|
|
2 2w |
|
|
|
2 2w |
|
|
||||||||||||||||||
D w |
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
q. |
(21) |
||||
|
|
y |
|
x |
|
|
|
|
|
x y x y |
|
|
x |
|
y |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Эти уравнения известны в теории упругости как уравнения Кар- |
|||||||||||||||||||||||||||||||
мана. Искомые функции |
б |
должны удовлетворять еще и гра- |
|||||||||||||||||||||||||||||
w |
и |
|
|
|
|
||||||||||||||||||||||||||
ничным условиям. |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
С |
|
1.5. Граничные условия |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для прямоугольной пластины каждой кромке должны соответствовать граничные условия. Для жестко защемленной или шарнирно опертой кромки пластинки при различных ограничениях на напряжения и перемещения в срединной поверхности граничные условия аналогичны условиям для пологих оболочек.
Граничные условия накладываются на функцию прогибов:
для жестко защемленной кромки: |
|
|||
w 0; |
w |
0; |
||
|
|
|||
для шарнирно опертой кромки: |
|
x |
|
|
|
2w |
|
||
w 0; |
|
0. |
||
|
x2 |
|||
|
|
|
||
Функция напряжений должна удовлетворять указанным ниже граничным условиям.
8
Если точки кромки, параллельной оси y , свободно смещаются
2
вдоль оси x , то x 0 или x2 0; если же – вдоль оси y, то
xy 0 или 2 0. Если точки кромки закреплены от перемеще-
x y
ний в направлении оси x , то u 0, а в направлении оси y, то v 0.
1.6. Метод последовательных приближений
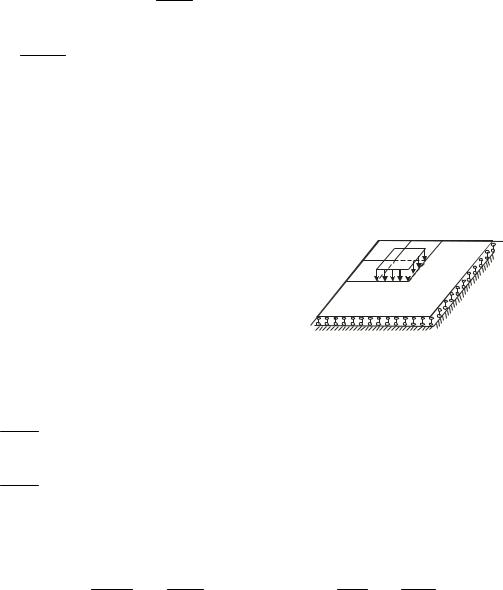
Применение метода последовательных приближений рассмотрим в задаче об изгибе прямоугольной пластины под воздействием на
ограниченном |
|
|
прямоугольном |
участке |
|
|
|
0 |
a1 a2 |
a x |
|||||||
равномерно |
|
распределенной |
|
нагрузки. |
|
|
b1 |
|
|
|
|||||||
Пластина опирается своими кромками на |
|
|
b2 |
q |
|
|
|||||||||||
|
|
|
|
|
|||||||||||||
абсолютно жесткие в своей плоскости |
|
|
|
|
|
|
|||||||||||
диафрагмы и абсолютно гибкие из нее, |
|
|
y b |
|
|
|
|||||||||||
чему соответствуют |
граничные |
условия |
И |
|
Рис. 3 |
|
|||||||||||
(рис. 3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
||||
|
2w |
|
|
|
|
|
|
|
|
|
|
|
|||||
w 0; |
0; |
|
Nx 0; v 0 |
(x 0, |
x a ); |
|
|
||||||||||
|
x2 |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
||
|
2w |
|
|
|
|
|
|
|
|
|
|
|
|
||||
w 0; |
0; |
|
Ny |
0; u 0 |
(y 0, |
y b). |
|
|
|||||||||
|
y2 |
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
||
Нагрузка q |
|
|
|
действует при a1 x a2 и b1 |
y b2 . Решение |
||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
||
системы уравнений (13) ищем в двойных тригонометрических рядах: |
|||||||||||||||||
|
|
|
|
|
const |
|
|
|
|
|
|
|
|
|
|
||
w w |
|
|
sinm x sinn y ; |
|
ij |
sini x sin j y . |
(22) |
||||||||||
|
mn |
|
|
|
|
|
b |
|
|
|
a |
|
b |
|
|||
|
m,n |
Сa |
|
|
i,j |
|
|
|
|
||||||||
Подстановка этих рядов в уравнения (21) с умножением первого
уравнения в (21) на sin |
i x |
sin |
j y |
, второго на |
sin |
m x |
sin |
n y |
с |
a |
|
a |
|
||||||
|
|
b |
|
|
b |
||||
последующим интегрированием по поверхности пластинки, согласно методу Бубнова–Галеркина, приводит к системе нелинейных алгебраических уравнений относительно искомых коэффициентов wmn ,
ij :
9

1 |
i2 |
|
j2 |
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i 1 I ; j 1 J ) ; |
|
|
||||||
|
|
|
|
2 |
|
|
2 |
|
ij |
|
2 2 |
|
|
2 w Aijw 0 |
|
(23) |
||||||||||||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
E a |
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
j |
2 2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
T |
|
|
|
4q |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
2 |
|
|
|
|
wmn 2 2 2 |
Bmnw |
6 qmqn |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m 1 M ;n 1 N ), |
(24) |
||||||||||
где qm |
|
|
2 |
sinm 0 sinm c |
;qn |
2 |
sinn 0 sinn c ; 0 |
a1 a2 |
; |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
2a |
|||||||
0 |
|
b1 b2 |
|
, c |
|
a2 |
a1 |
|
, c |
|
|
b2 b1 |
. Векторы (матрицы-столбцы) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2b |
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
2b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
w , содержат в качестве своих элементов в определенном порядке коэффициенты рядов (22). Матрица Aij – квадратная, содержит M N
строк и столько же столбцов. Матрица |
Bmn – прямоугольная, имеет |
||||||||||||||||||||||||||||||||||
I J строк и M N столбцов. Элемент матрицы Aij |
|
на пересечении |
|||||||||||||||||||||||||||||||||
строки с номером |
k (m 1) N n |
|
|
и |
|
|
|
|
столбца |
|
|
с |
|
|
|
номером |
|||||||||||||||||||
|
|
|
|
|
|
А |
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
k1 (m1 1) N n1 вычисляется так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Aij(k,k1) mnC m,m1,i C n,n1,j m1n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
|
|
|
(25) |
||||||
|
|
|
|
|
|
m |
2S mД,m ,i S n,n ,j n |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
и |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
Элемент матрицы Bmn |
с индексами k (i 1) I j , |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
k1 (m1 1) N n1: |
2S i,m ,m S j,n ,n m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
B |
mn |
(k,k ) j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . (26) |
||||
|
|
|
2ijC i,m ,m C j,n ,n m n |
i2S i,m ,m S j,n ,n n |
|||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
1 |
1 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|||
В (25) и (26) обозначены определенные интегралы: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2k(i |
2 |
j |
2 |
k |
2 |
) |
|
|
|
|||||||||||
C(i,j,k)Сcosi cos j sink d |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
4i |
2 |
j |
2 |
(i |
2 |
j |
2 |
k |
2 2 |
|
|||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
||||||||||||||
|
|
|
|
(i j k 2m ; m 1,2,3 ); |
|
|
|
|
|
|
|
|
|
(27) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4ijk |
|
|
|
|
|
|
|
|
|
|||||
S(i,j,k) sini sin j sink d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4i |
2 |
j |
2 |
|
|
(i |
2 |
j |
2 |
k |
2 2 |
|
|
|||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
||||||||||||
|
|
|
|
(i j k 2m ; m 1,2,3 ). |
|
|
|
|
|
|
|
|
(28) |
||||||||||||||||||||||
Если сумма индексов i j k равна четному числу или нулю, интегралы в (27) и (28) равны нулю.
Систему уравнений (23), (24) можно решать последовательными приближениями в следующем порядке:
10
