Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

нелинейные задачи по строительной механики.pdf

Скачиваний:

Добавлен:

10.03.2016

Размер:

1.5 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Министерство образования и науки Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Сибирская государственная автомобильно-дорожная академия (СибАДИ)»

Кафедра «Строительная механика и геотехнологии»

НЕЛИНЕЙНЫЕЗАДАЧИ
СТРОИТЕЛЬНОЙМЕХАН КИ
				И
Методические указания
			Д
к выполнению расчетно-графических работ
		А
	б
остав тель Г.М. Кадисов
и
С

Омск 2015

УДК 624.04 ББК 38.112 Н49

Рецензент д-р техн. наук, доц. Ю.В. Краснощеков (СибАДИ)

Работа утверждена редакционно-издательским советом СибАДИ в качестве методических указаний.

Н49 Нелинейные задачи строительнойСибАДИмеханики [Электронный ресурс] : методические указания к выполнению расчетно-

графических работ / сост. Г.М. Кадисов. – Электрон. дан. − Омск : СибАДИ, 2015. – Режим доступа: http://bek.sibadi.org/fulltext/ESD44.pdf , свободный после авторизации. – Загл. с экрана.

ISBN 978-5-93204-829-0

Изложены теория расчета гибких прямоугольных пластин под воздействием равномерно распределенной на локальной прямоугольной площадке внешней нагрузки и методика расчета стержневой рамы по предельным состояниям с учетом возникновения пластических шарниров. Даны примеры расчета. В приложениях приведены перечни параметров исходных данных для выполнения студенческих работ.

Имеют интерактивное оглавление в виде закладок.

Предназначены обучающимся по специальности «Строительство уникальных зданий и сооружений».

Текстовое (с мвольное) издание (6,0 МБ)

Системные требован я : Intel, 3,4 GHz ; 150 МБ ; Windows XP/Vista/7 ; DVD-ROM ;

1 ГБ свободного места на жестком д ске ; программа для чтения pdf-файлов Adobe Acrobat Reader

Редактор Н.И. Косенкова Техническая подготовка Т.И. Кукина

Издание первое. Дата подписания к использованию 11.09.2015

Издательско-полиграфический центр СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПЦ СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1

Введение

При изучении дисциплины «Нелинейные задачи строительной механики» студенты должны выполнить два задания. В первом задании необходимо определить прогибы и внутренние усилия в прямоугольной гибкой пластине под воздействием поперечной нагрузки, равномерно распределенной на ограниченной области. Во втором задании нужно решить задачу с определением предельной нагрузки, действующей на плоскую раму. Исходные данные для выполнения расчетно-графических работ приведены в приложениях.

1.ИЗГИБ ПРЯМОУГОЛЬНОЙ ГИБКОЙ ПЛАСТИНЫ

1.1.ДеформацииИ

Вслучае, когда прогиб пластиныДпревышает 1/5…1/2 ее толщины, такую пластину следует рассматривать как гибкую, в которой вместе с изгибными возникаютАцепные (мембранные) напряжения, равномерно распределенные по ее толщине. Им соответствуют де-б


нормали и гипотеза о ненадавливаемо-	dy		u v
сти горизонтальных слоев. Деформа-	C	w
ции срединной поверхности, принимая y	z	A1
ции срединной поверхности, принимая y	z	A1

перемещения u и vималыми, прогиб		d
перемещения u и vималыми, прогиб	Y	X
w конечным, сопоставимым с толщи-	Y
w конечным, сопоставимым с толщи-	d
ной пластины, определим, исходя из		B1
С	C1
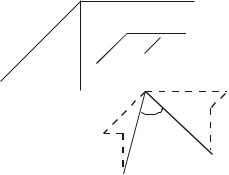
рис.1, на котором показаны волокна	Рис.1
AB, AC, расположенные на средин-	Рис.1

ной поверхности до деформации параллельно координатным осям. После деформации они перемещаются

в новое положение A1B1, A1C1,			их длины dX , dY и угол между
ними изменились:			dY dy dy (1 y)dy.
dX dx dx (1 x )dx ;
B AC 90o 0 ,				(1)
1	1	1

где 0 – угол сдвига, угол отклонения от прямого угла между рассматриваемыми волокнами после деформации.

На рис.1 штриховыми линиями показаны проекции на оси коор-

динат векторов A1B1 ,													A1C1 , представленных в компонентах:
					dx									x	u						1 u/ x
		p
A B											v
A B											v													v/ x dx ;
1 1										x														w/ x
							xw																	w/ x
									yu															u/ y


	A1C1 q dy yv																			1 v/ y														dy.
								yw																w/ y
								yw																w/ y
	Из (1) можно получить квадраты длин dX , dY :
(dX)2 (dx dx)2 (dx)2[1 2 x(1																																							1		x )];
(dX)2 (dx dx)2 (dx)2[1 2 x(1																																									x )];
																																						2
(dY)2 (dy dy)2 (dy)2[1 2 y(1																																								1	y )].
(dY)2 (dy dy)2 (dy)2[1 2 y(1																																									y )].
																							А															2
																							А											dYИ:
	Из (2) получим квадраты длин dX ,																																	dYИ:
2					2								u				2					v					2			w					2
(dX)			(dx)				{(1									)			(						)			(						)				}
(dX)			(dx)				{(1						x			)			(			x			)			(						)				}
						u							x									x							Дx
		2				u								u 2									v					2			w						2						;
(dx) {1				2								(						)		(							)		(						) }
(dx) {1				2		x						(		x				)		(			x				)		(		x				) }
						x								x									x								x
2					2								v				2					u					2			w					2
(dY)			(dy)				{(1									)			(							)			(					)				}
(dY)			(dy)				{(1									)			(							)			(	y				)				}
						v							yбy																	y													.
		2				v								v			2						u					2			w						2						.
(dy) {1 2												(					)			(								)	(							) }
(dy) {1 2						y						(					)			(			y					)	(		y					) }
						y		иy															y								y
	Скалярное произведение векторов																																									,			:
	Скалярное произведение векторов																																A1B1									,		A1C1	:
					С

					A B AC A B AC cos pТq .
					1		1							1		1						1			1				1			1

(dx udx)( udy) ( vdx)(dy vdy) ( wdx)( wdy).

x	y		x	y	x			y
Из (3) найдем длины dX , dY (приближенно):
dX [1 x(1		1	x )]dx;	dY [1 y	(1	1	y )]dy.
		2
					2

(2)

(3)

(4)

(5)

(6)

Теперь, приравнивая правые части первых формул (3) и (4), а затем и вторых, после несложных сокращений получим

u 1

u 2

v 2

w 2

x(1

x )

{(

)

(

)

(

) };

v 2

u 2

w 2

y(1

{(

)

(

) (

) }.

(7)

Подставляя длины dX , dY (6) взамен

A1B1, A1C1

в равенство

(5), можно получить

x ) y(1

y )cos

(

).(8)

x y

Полагая, что относительные линейные деформации в срединной

плоскости малы ( x

1, y

1), а прогиб w значительно больше про-

дольных перемещений u ,v , выражения в скобках в левых частях формул (7) и (8) можно принять равными единице, а в скобках правых частей оставить только производные от w . В результате получим деформации в срединной плоскости:

w 2

v 1 w 2

w w

;

. (9)

2 x

x y

Эти деформации удовлетворяют условию совместности:

x y

2 .

(10)

x y

Кривизны и кручение срединной поверхности, как и в жесткой

пластине:

;

(11)

x y

определяются деформа-

Деформации в точке с координатой z

циями срединной поверхностиии изгибом пластины:

z ;

z .

(12)

x y

1.2. Уравнения равновесия

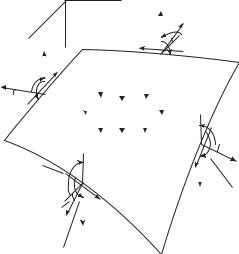
Для составления уравнений равновесия на рис.2 показан элемент пластинки с размерами в плане dx,dy в деформированном состоянии с действующими на его гранях внутренними усилиями и внешней нагрузкой на поверхности.

Спроецировав все силы сначала на ось x :

	N	x		S
Nx		x	dx dy Nxdy S		dy dx Sdx 0,
Nx	x		dx dy Nxdy S	y	dy dx Sdx 0,
	x			y

получим после несложных сокращений первое уравнение равновесия:

Nx	S	0;	(13)

x	y

азатем, проектируя все силы на ось y, получим аналогично второе:

xQy

dxИx

Рис. 2

(14)

бx y

Третье уравнен е равновесия – сумма проекций всех сил на ось

z – составим последовательно. Сначала сложим проекции поперечных сил на ось z :

QСdy (Q

dx)dy Q

dx (Q

dy)dx

dxdy,

затем продольных сил

Nxdy	w	(Nx	Nx		dx)(	w	2w	dx)dy
	x		x			x	x2

Nydx	w	(Ny	Ny	dy)(		w	2w	dy)dx
	y		y			y	y2

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.05.20152.27 Mб14МУ2 по КР для ЗО.doc
#
13.08.201920.77 Mб77МУ2 по лаб Сист.doc
#
02.05.2015483.07 Кб54МУ_ПП_ЛР.pdf
#
02.05.20151.94 Mб47настройка роутера.docx
#
02.05.2015514.05 Кб11НГ.doc
#
10.03.20161.5 Mб33нелинейные задачи по строительной механики.pdf
#
08.07.2019762.37 Кб16Неторопливая элегантность движений.doc
#
10.09.20192.51 Mб2Новые тесты по информатике.doc
#
02.05.201572.19 Кб14Нормы амортизации.doc
#
05.11.2018366.06 Кб42О.В. Кобзеева.docx
#
10.03.20166.65 Mб18Оборудование нефтепродуктообеспечения и газоснабжения .pdf