PDF (Сергеева - инж. гр.) (Учебник 1)

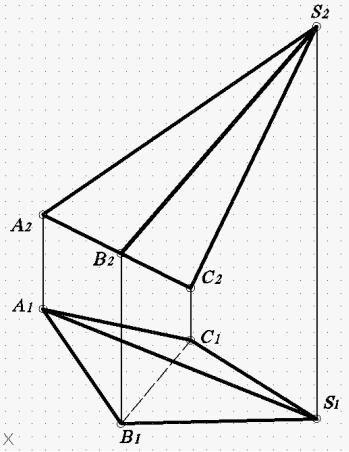
Построить: сечение пирамиды SABC плоскостью . 1. Решение выполнить:

– с использованием горизонтали плоскости в слое 1;

– с использованием фронтали плоскости в слое 2.

2.Проверить правильность решения задачи путем сравнения результатов решения с использованием команды «Слой».

3.Сравнить способы решения задачи и сделать вывод.

Рис. 69. Заданная пирамида (вариант 7)

Вариант 7

Дано: пирамида (рис. 69) SABC (S1А1 В1С1; S2 А2 В2С2). S1(176;97); S2(176;246); A1(74;139); A2(74;175); B1(103;95); B2(103;160); C1(129;127); C2(129;147).

Построить: натуральные величины ребер пирамиды SABC. 1. Решение выполнить:

–с использованием метода замены плоскостей проекций;

–сиспользованиемметодавращениявокругпроецирующейпрямой;

–с использованием метода прямоугольного треугольника.

51

2.Проверить правильность решения задачи наиболее возможным количеством способов.

3.Сравнить способы решения задачи и сделать вывод.

Вариант 8

Дано: плоскость ABC (А1В1С1; А2В2С2). A1(67;142); A2(67;188); B1(92;100); B2(92;235); C1(130;115); C2(130;202).

Построить: натуральную величину плоскости ABC. 1. Решение выполнить:

–с использованием метода вращения вокруг прямой уровня (фронтали);

–с использованием метода вращения вокруг прямой уровня (горизонтали).

2. Выбрать и обосновать наиболее удобный и полезный способ последовательности построений.

3. Проверить правильность решения задачи наиболее удобным способом.

4. Сравнить результаты решения задачи заданными методами и сделать вывод.

Решение

Прежде всего, следует определить, в каком порядке решать задачу обоими способами. Рассмотрим возможные варианты.

Можно решать поочередно задачу 1-м способом в одном файле, затем 2-м способом в другом.

Можно решать в той же очередности, но в одном файле и в разных слоях, чтобы скопировать один результат и наложить на другой для сравнения. Однако следует учесть тот факт, что результаты решения без поворота одного из них нельзя будет наложить для их сравнения. В этом случае удобно измерить площади построенных натуральных величин и сравнить.

И, наконец, предлагается третий вариант порядка решения: выполнять построения в одном файле параллельно таким образом, чтобы каждый этап решения 1-м способом сразу повторялся для решения 2-м способом. Преимущества этого порядка построений очевидны.

Во-первых, легче использовать логическое разнообразие цветов. Во-вторых, повторение решения удобно для закрепления материала, кроме того, повторение идентичных этапов помогает лучше сосредоточиться, что способствует снижению вероятности ошибочных по-

52

строений и в конечном итоге ускорению решения обоими способами. Помимо этого, постоянное переключение с одного способа на другой и сравнение идентичности построений способствует развитию внимательности, памяти, логического мышления и умения анализировать.

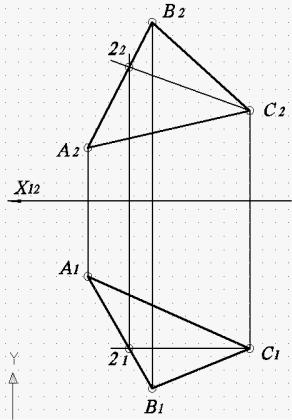
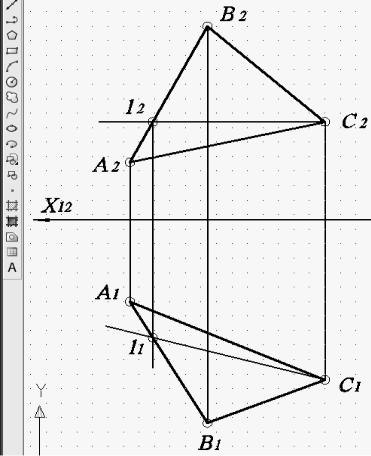
Начальные построения выполняются в одном файле с использованием команды «Отрезок» и клавиатуры. Затем с использованием команд «Цвет» и «Отрезок», режима «ОРТО» и постоянного режима объектной привязки «Пересечение» вводится для решения 1-м способом в плоскости фронталь f (рис. 70), а для решении 2-м способом – горизонталь h (рис. 71).

Выбирается точка В для вращения вокруг линий уровня. Для этого первым способом через проекцию точки В2 строится с использованием режима объектной привязки «Нормаль» проекция фронтально проецирующей плоскости 2 перпендикулярно f2 (рис. 72). Аналогично для решения 2-м способом через проекцию точки В1 строится с использованием режима объектной привязки «Нормаль» проекция горизонтально проецирующей плоскости ψ1 перпендикулярно h1 (рис. 73). Для обоих способов определяются центры вращения – точка О (рис. 72) и точка Р (рис. 73), и проекции радиусов вращения – О1В1 и О2В2, Р1В1 и Р2В2.

Рис. 70. Ввод фронтали в плоскости

53

Для определения натуральных величин радиусов вращения используется метод прямоугольного треугольника. При построении 1-м способом копируется разность глубин точки В и фронтали f (отрезок В1L, рис. 72) в проекцию центра вращения О2. Затем на проекции фронтали f2 откладывается отрезок В1L (О2R, рис. 72) с использованием команды «Круг» и режима объектной привязки «Конточка». Такое построение описано в решении задачи вариантом 1. При решении 2-м способом аналогично копируется разность высот радиуса вращения В2М и откладывается на проекции горизонтали h1 (отрезок P1N, рис. 73). Для обоих способов выполняются построения натуральных величин радиусов вращения (В2R, рис. 72) и (В1N, рис. 73).

Затем для решения 1-м способом натуральная величина радиуса вращения откладывается от проекции центра вращения О2 на проекции плоскости 2 с использование команд «Копировать», «Круг» и режима объектной привязки «Конточка» (О2В’2, рис. 74). Для решения 2-м способом аналогично откладывается натуральная величина радиуса вращения от проекции центра вращения Р1 на проекции плоскости ψ1 (Р1В’1, рис. 75).

Рис. 71. Ввод горизонтали в плоскости

54

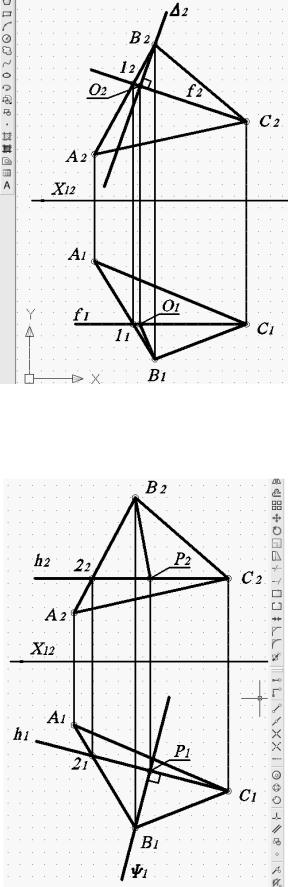
Рис. 72. Построение проекции фронтально проецирующей плоскости 2

Рис. 73. Построение проекции горизонтально проецирующей плоскости ψ1

55

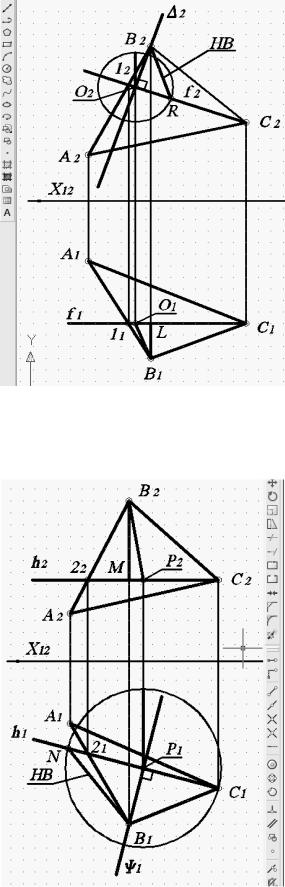
Рис. 74. Построение натуральной величины радиуса вращения В2R

Рис. 75. Построение натуральной величины радиуса вращения В1N

56

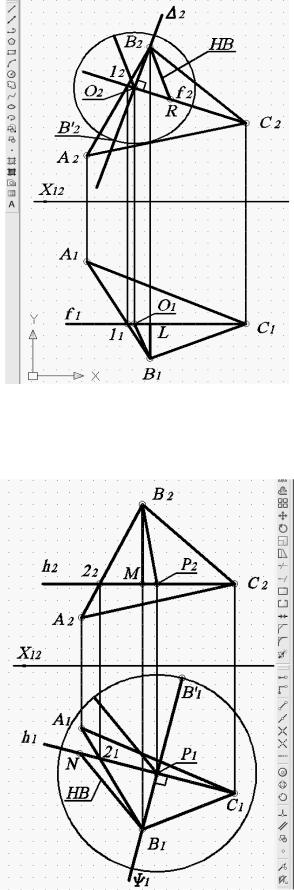
Рис. 76. Построение натуральной величины радиуса вращения О2В’2

Рис. 77. Построение натуральной величины радиуса вращения Р1В’1

57

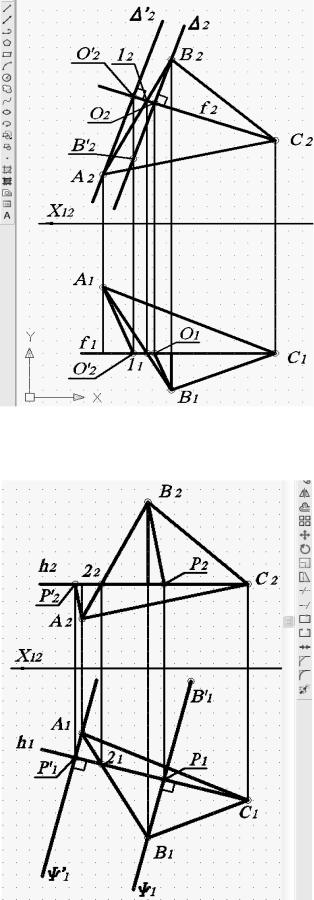
Рис. 78. Построение проекции плоскости ’2

Рис. 79. Построение проекции плоскости ψ’1

58

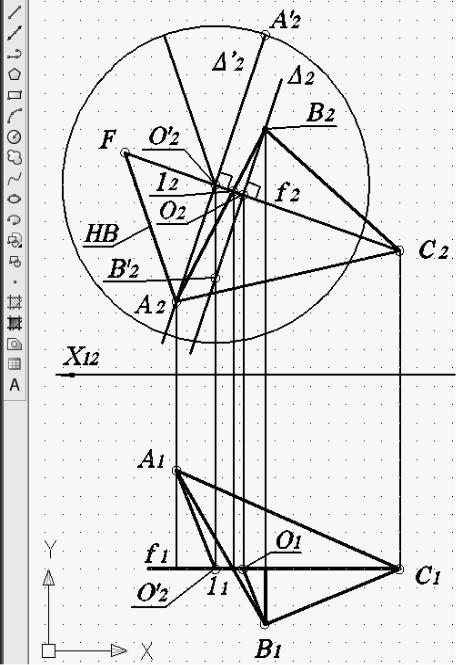
Решение задачи 1-м и 2-м способом продолжается построениями для вращения точки А вокруг линий уровня. Для 1-го способа вводится проекция плоскости, в которой вращается точка А ( ’2, рис. 78), а для 2-го способа вводится проекция плоскости ψ’1 (рис. 79). Последующие построения повторяются аналогично построениям для вращения точки В и заканчиваются построениями отрезков О’2A’2 для 1- го способа, Р’1A’1 для 2-го способа (рис. 80, 81).

Рис. 80. Построение отрезков О’2A’2

59

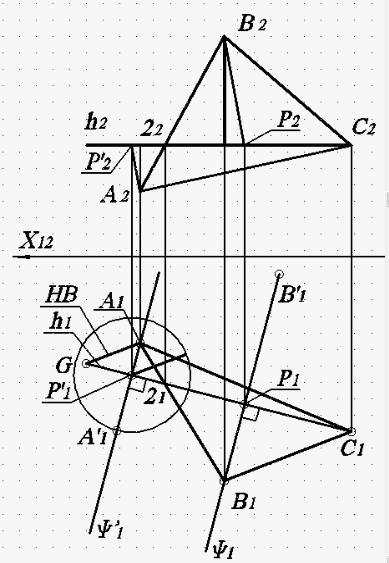
Рис. 81. Построение отрезков Р’1A’1

Наконец, для обоих способов выполняются построения конечных результатов (натуральных величин плоскостей) с использованием команды «Отрезок» путем соединения новых проекций точек A’1,

В’1 и С1 (рис. 82, 83).

Как предполагалось, новые проекции для построений 1-м и 2-м способом повернуты относительно друг друга. Измеряются площади обоих результатов поочередно.

Результаты измерения площадей треугольников, построенных 1-м и 2-м способом и форматы командной строки выполнения команды «Площадь» приведены на рис. 84 и 85.

Измерения площади совпадают с точностью до 4-го знака. Сравнение измерений площади натуральной величины плоскости, построенной обоими методами, показывает, что задача решена верно.

60