
PDF (Сергеева - инж. гр.) (Учебник 1)
.pdf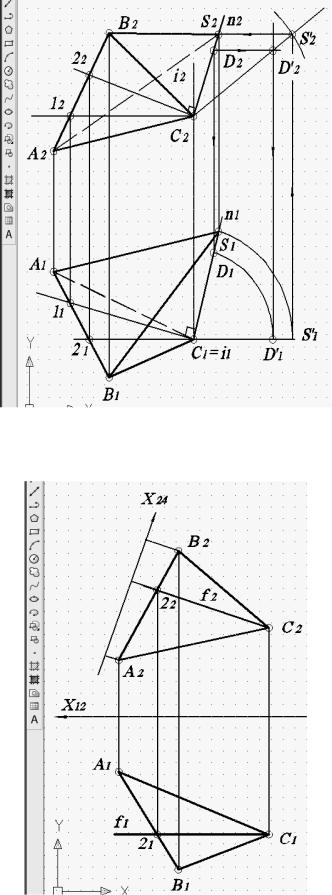
Рис. 54. Результат построения пирамиды первым способом
Рис. 55. Замена плоскости проекций с использованием фронтали
41
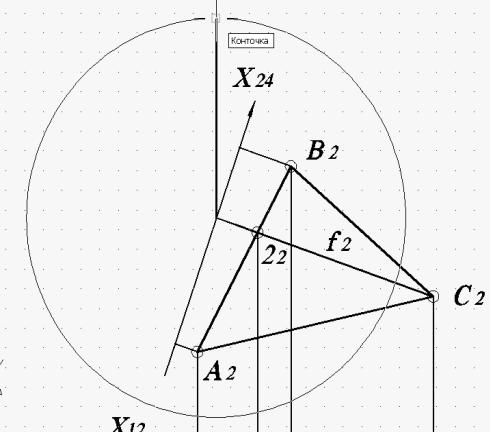
При использовании способа замены плоскостей проекций в данном примере замещается горизонтальная плоскость проекций П1 на новую плоскость проекций П4. Для этого в плоскости АВС вводится фронталь f (рис. 55), а новая ось X14 и новые линии связи вводятся перпендикулярно фронтальной проекции фронтали f2. При этом используется режим объектной привязки «Нормаль».
Для построения проекций основания пирамиды и ее ребра от точек пересечения линий связи и оси X14 глубины точек А, В и С откладываются с использованием команд «Копировать», «Круг» и «Удлинить» («Обрезать»). Команда «Круг» выполняется с применением режима объектной привязки «Конточка» (рис. 56). Глубины точек рекомендуется выделить цветом, отличным от других цветов, используемых в данном примере.
Рис. 56. Построение проекции точки С4
Выполнение команды «Удлинить» при указании удлиняемого объекта для построения проекции точки С4 показан на рис. 57. Построение проекций точек А4 и В4 выполняется аналогично. Результат построения проекции основания А4С4В4 приведен на рис. 58.
42
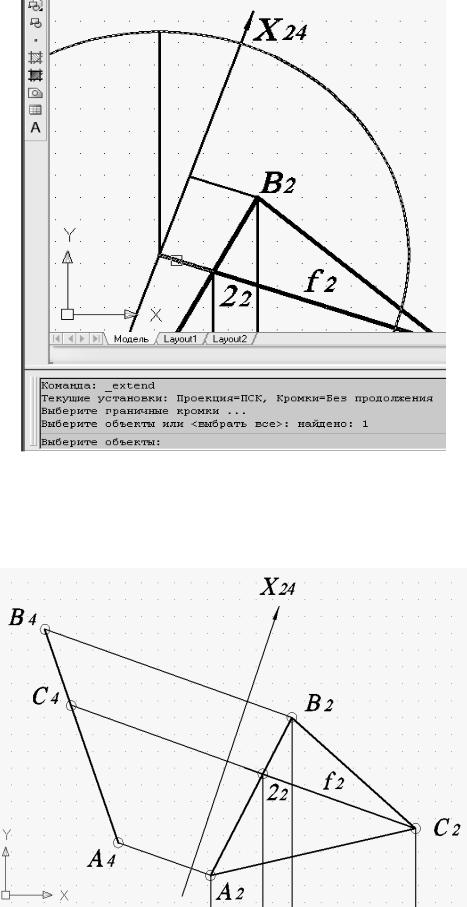
Рис. 57. Указание удлиняемого объекта при выполнении команды «Удлинить» для построения проекции точки С4
Рис. 58. Результат построения проекции основания А4С4В4
43
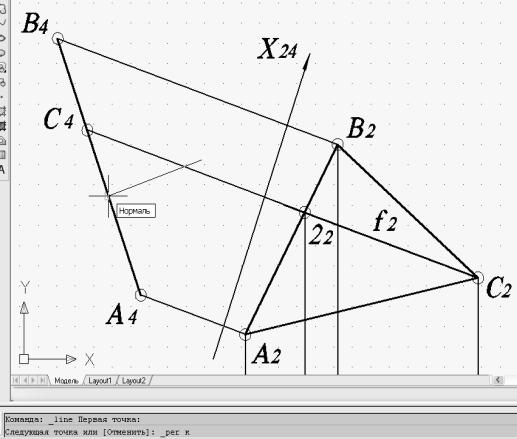
Построение проекции ребра S4С4 выполняется в 4 этапа. Сначала строится из произвольной точки перпендикуляр к проекции основания пирамиды А4С4В4 (рис. 59). Перпендикуляр переносится с использованием команды «Переместить» в проекцию точки С4. Затем строится круг с использованием команды «Круг» с центром в С4 радиусом 55 (рис. 60), до которого перпендикуляр либо удлиняется («Удлинить»), либо обрезается («Обрезать»). Наконец, круг удаляется командой «Стереть». Результат построения проекции ребра S4С4 приводится на рис. 61.
Рис. 59. Построение перпендикуляра к проекции основания пирамиды
Затем производится построение проекции вершины S2. Проекция ребра S4С4 является натуральной величиной, а значит, линией уровня. Поэтому на фронтальной плоскости проекций она должна быть параллельна оси X14. Построение ее начинается копированием оси X14 в С2 (рис. 61, отрезок а). Линия связи строится перпендикулярно оси X14 до пересечения с отрезком а (рис. 61, S2). Результат построения проекции ребра S2С2 показан на рис. 62.
44
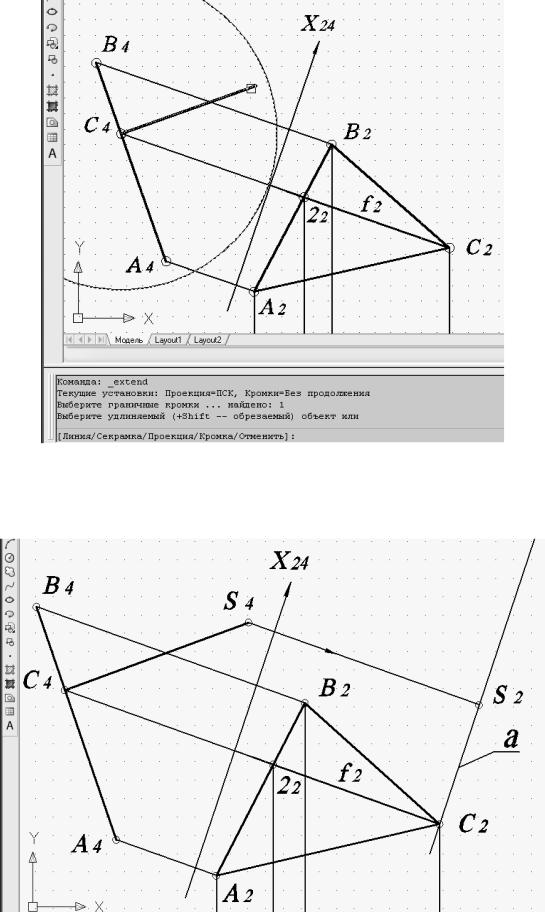
Рис. 60. Указание удлиняемого перпендикуляра при построении проекции ребра пирамиды S4С4
Рис. 61. Копирование оси и построения проекции S2
45
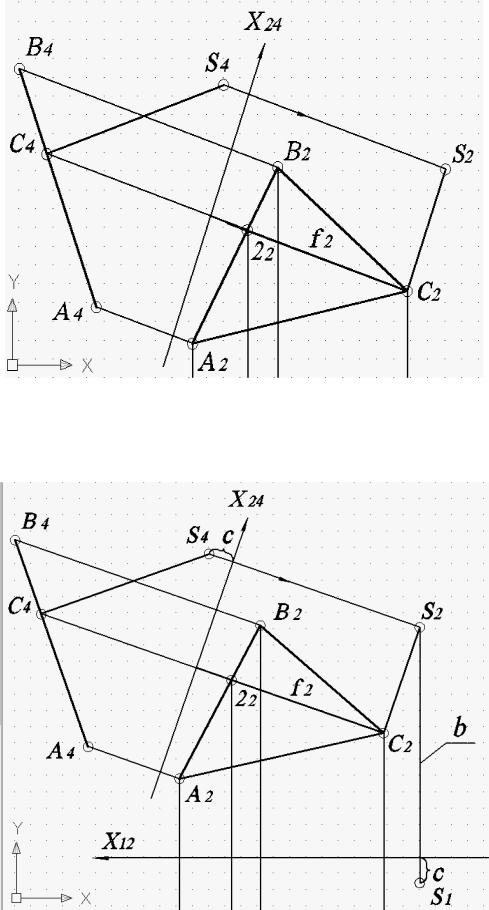
Рис. 62. Результат построения проекции ребра S2С2
Рис. 63. Построение проекции вершины пирамиды S1
46
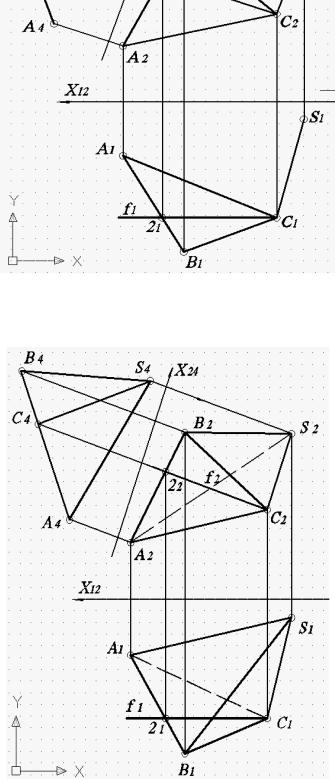
Рис. 64. Результат построения проекции ребра S1С1
Рис. 65. Результат построения пирамиды вторым способом
Для построения проекции вершины пирамиды S1 проводится линия связи от S2 с использованием режима «ОРТО» (рис. 63, отрезок b), координата S4 копируется в точку пересечения оси X12 и линии связи
47
(рис. 63, отрезок c). Построение проекции точки S1 выполняется аналогично построению проекций точек С4, В4, А4. Результат построения проекции ребра S1С1 показан на рис. 64. На рис. 65 показан результат построения всех проекций пирамиды вторым способом с использованием команд «Отрезок» и «Тип линии».
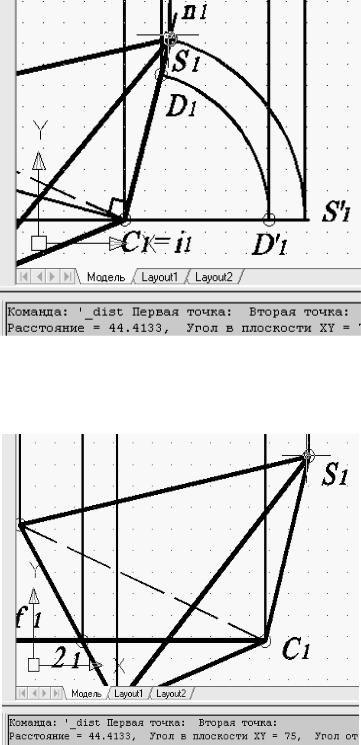
Рис. 66. Измерение проекции ребра, построенного первым способом
Рис. 67. Измерение проекции ребра, построенного вторым способом
48
Сравнение результатов решения задачи обоими способами выполняется измерением проекции ребра S1С1 с использованием команды «Расстояние» (рис. 66, 67).
Вариант 2
Дано: основание пирамиды АВС (А1В1С1; А2В2С2). А1(67;142);
А2(67;188); В1(92;100); В2(92; 235); С1(130;115); С2(130; 202).
Построить: пирамиду с ребром АS, перпендикулярным АВС, длиной 50.
1. Решение выполнить:
–с использованием теоремы о проекции прямого угла и метода прямоугольного треугольника;
–с использованием метода замены плоскостей проекций.
2.Проверить правильность решения задачи путем сравнения результатов решения с применением команды «Площадь».
3.Сравнить способы решения задачи и сделать вывод.
Вариант 3
Дано: основание пирамиды АВС (А1В1С1; А2В2С2). А1(67;142);
А2(67;188); В1(92;100); В2(92; 235); С1(130;115); С2(130; 202).
Построить: пирамиду с ребром ВS, перпендикулярным АВС, длиной 60.
1. Решение выполнить:
–с использованием теоремы о проекции прямого угла и метода прямоугольного треугольника;
–с использованием метода замены плоскостей проекций.
2.Проверить правильность решения задачи путем сравнения результатов решения с применением команды «Копировать».
3.Сравнить способы решения задачи и сделать вывод.
Вариант 4
Дано: плоскость АВС (А1В1С1; А2В2С2). А1(67;142); А2(67;188); В1(92;100); В2(92; 235); С1(130;115); С2(130; 202).
Построить: натуральную величину плоскости АВС.
1.Решение выполнить:
–с использованием метода замены плоскостей проекций;
–сиспользованиемметодавращениявокругпроецирующейпрямой.
2.Проверить правильность решения задачи путем сравнения результатов решения любыми двумя способами.
3.Сравнить способы решения задачи и сделать вывод.
49
Вариант 5
Дано: плоскость АВС (А1В1С1; А2В2С2). А1(44;106); А2(44;206); В1(90;146); В2(90;230); С1(109;124); С2(109;196). Точка М(М1; М2). М1(74;98); М2(74;238).
Построить: точку N, симметричную точке М. 1. Решение выполнить:
–с использованием теоремы о проекции прямого угла в слое 1;
–с использованием метода замены плоскостей проекций в слое 2. 2. Проверить правильность решения задачи путем сравнения ре-
зультатов решения с использованием команды «Слой».
3. Сравнить способы решения задачи и сделать вывод.
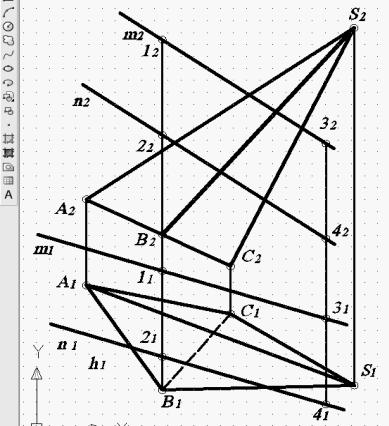
Рис. 68. Заданная пирамида (вариант 6)
Вариант 6
Дано: пирамида (рис. 68) SABC (S1А1 В1С1; S2А2 В2С2) и плос-
кость (m n). m (m1; m2). n (n1; n2). 1 и 3 m. 2 и 4 n. S1(176;97); S2(176;246); A1(74;139); A2(74;175); B1(103;95); B2(103;160); C1(129;127);
C2(129;147); 11(103;145); 12(103;242); 21(103;109); 22(103;202); 31(165;125); 32(165;198); 41(165;89); 42(165;158).
50
