
- •Введение
- •Некоторые сведения о методиках динамического расчета артиллерийских орудий
- •Глава 1 математическая модель действия выстрела на артиллерийское орудие
- •1.1. Выбор и обоснование расчетной схемы
- •1.2 Анализ конструкций современных образцов артиллерийских орудий
- •Глава 2
- •Движение при наличии связей.
- •Уравнения лагранжа второго рода при нестационарном базисе
- •Основные понятия
- •2.1. Несвободное движение точки.
- •2.2 Связи и их классификация
- •2.3.Возможные и виртуальные перемещения
- •2.4 Обобщенные координаты. Число степеней свободы механической системы
- •В различных случаях
- •2.5. Несвободное движение системы материальных точек
- •2.6. Виртуальная работа силы. Идеальные связи
- •2.7. Обобщенные силы
- •2.8. Уравнения Лагранжа второго рода
- •2.9. Последовательность действий при использовании уравнений Лагранжа второго рода для решения задач о движении голономных систем с несколькими степенями свободы
- •Движении:
- •3.2. Углы Эйлера.
- •3.3.Формулы преобразования координат. Поворотные матрицы
- •3.4. Мгновенная угловая скорость и угловое ускорение Кинематические уравнения Эйлера
- •3.5. Скорость и ускорение точек тела. Формула Ривальса
- •Расчетная работа № 1 – Тема: кинематика вращения твердого тела вокруг неподвижной точки случай регулярной прецессии
- •4.1. Схемы конструкций и таблица к ним с исходными данными к расчетной работе «№1»
- •4.2.Методические указания и план решения расчетной работы № 1
- •4.3. Пример 4.1решения расчетной работы № 1 (рис.4.3). Тема: вращение твердого тела вокруг неподвижной точки
- •4.4. Пример 4.2 решения расчетной работы №1 (рис.4.4). Тема: вращение твердого тела вокруг неподвижной точки
- •5.2. Пример 5.1 выполнения второй расчетной работы №2
- •Курсовая работа тема:
- •Расчет динамических моделей объектов вооружения
- •Конкретных конструктивно компоновочных схем по учебной дисциплине «динамика конструкций»
- •.Методические указания и примеры выполнения
- •Пример 6.2 выполнения расчетной работы по динамике несвободной механической системы с тремя степенями свободы (рис.6.3.1)
- •Окончательный вид уравнений Лагранжа второго рода или дифференциальные уравнения движения рассматриваемой системы в обобщенных координатах
- •Пример 6.3 выполнения расчетной работы по динамике несвободной механической системы с тремя степенями свободы
- •Литература Основная литература
- •Дополнительная литература
- •Глава 3. Вращение твердого тела вокруг неподвижной точки .44
- •Глава 4. Расчетная работа № 1–тема: вращение твердого
4.2.Методические указания и план решения расчетной работы № 1
Случай регулярной прецессии это такое вращение твердого тела вокруг неподвижной точки, при котором (рис.4.2) во все время движения остаются постоянными:
угол нутации
![]()
![]()
угловые скорости прецессии, ротации
и мгновенная угловая скорость
![]()
![]()
![]()
угловое ускорение
![]()
1 .
Найти неподвижную точку вращающегося
тела, выбираемую за начало отсчета
неподвижной и связанной координатных
систем. Выбрать оси прецессии -
.
Найти неподвижную точку вращающегося
тела, выбираемую за начало отсчета
неподвижной и связанной координатных
систем. Выбрать оси прецессии -![]() , ротации -
, ротации -![]() ,
нутации -
,
нутации -![]() (
(![]()
![]() или
или![]()
![]() ).
).
2. Определить угловые скорости прецессии
![]() ,
нутации
,
нутации![]() ,
ротации
,
ротации![]() ,
мгновенную угловую скорость
,
мгновенную угловую скорость![]() и мгновенную ось вращения
и мгновенную ось вращения![]() .
.
В зависимости от задания движения
твердого тела вектор
![]() можно найти двумя способами:
можно найти двумя способами:
Рис.4.2
─1) определить
![]() по ее составляющим
по ее составляющим
![]() =
=![]() +
+![]() +
+![]() ;
;
─2) использовать мгновенную ось вращения
![]() , которую в дальнейшем будем для краткости
обозначать
, которую в дальнейшем будем для краткости
обозначать![]() .
По известной скорости
.
По известной скорости![]() какой-либо точкиМ твердого
тела и положении оси
какой-либо точкиМ твердого
тела и положении оси![]()
![]() находят величину
находят величину![]() :
:![]() ,
где
,
где![]() ─ перпендикуляр, опущенный из точкиМ
на ось
─ перпендикуляр, опущенный из точкиМ
на ось![]()
![]() .
.
3. Определить угловое ускорение
![]() твердого тела. В случае регулярной
прецессии
твердого тела. В случае регулярной
прецессии![]() и является закрепленным в точкеОвектором, положительное направление
которого определяется как результат
векторного произведения.
и является закрепленным в точкеОвектором, положительное направление
которого определяется как результат
векторного произведения.
4. Определить скорости произвольных
точек твердого тела по формуле
![]() ,
величина скорости равна
,
величина скорости равна![]() .
.
5. Определить ускорения произвольных
точек твердого тела. Ускорение
![]() любой точки твердого тела следует
определить по формуле
любой точки твердого тела следует
определить по формуле
![]()
![]() +
+![]() ,
,
где
![]() =
=![]() ─
осестремительное ускорение, величина
его
─
осестремительное ускорение, величина
его
![]() =
=![]() ,
,
![]() =
=![]() ─
вращательное ускорение, величина
которого
─
вращательное ускорение, величина
которого![]() =
=![]() .
.
Так как
![]() всегда направлено от точки по
всегда направлено от точки по![]() к оси
к оси![]()
![]() ,
можно не пользоваться векторной формой
для
,
можно не пользоваться векторной формой
для![]() .
Что же касается
.
Что же касается![]() ,
то его следует находить только по
векторной форме.
,
то его следует находить только по
векторной форме.
Поскольку, при вращении около полюса
вектор
![]() не коллинеарен
не коллинеарен![]() ,
то
,
то![]() и
и![]() ,
вообще говоря, не являются перпендикулярными
векторами, поэтому определение
,
вообще говоря, не являются перпендикулярными
векторами, поэтому определение![]()
![]() +
+![]() должно производиться после построения
векторов на чертеже, и величина ускорения
будет равна
должно производиться после построения
векторов на чертеже, и величина ускорения
будет равна
![]()
![]() .
.
Для точек, лежащих на оси ротации твердого тела, справедливы также следующие зависимости:
![]() и
и![]()
![]() +
+![]() ,
,
где
![]() ─ нормальное ускорение;
─ нормальное ускорение;![]() ─
касательное ускорение, при регулярной
прецессии
─
касательное ускорение, при регулярной
прецессии![]() = 0.
= 0.
Все векторы, лежащие в плоскости OXY (плоскости чертежа), должны быть изображены в этой плоскости; направление же других векторов должно быть указано в тексте.
4.3. Пример 4.1решения расчетной работы № 1 (рис.4.3). Тема: вращение твердого тела вокруг неподвижной точки
случай регулярной прецессии.
Конус 1 с углом 2=60при вершине катится по неподвижному
конусу 2 с углом 2=120при вершине без скольжения, при этом
вершинаОконуса 1остается неподвижной,
а центр С его основания движется по
окружности, расположенной в горизонтальной
плоскости, с постоянной скоростью![]() ,
,![]() в данный момент времени (рис.4.3).
в данный момент времени (рис.4.3).![]() ,ОА=ОВ=2м.
,ОА=ОВ=2м.
Определить:1. Угол нутации,
угловую скорость нутации![]() ,
прецессии
,
прецессии![]() ,
ротации
,
ротации![]() и мгновенную угловую скорость
и мгновенную угловую скорость![]() .
.
2. Угловое ускорение конуса
![]() .
.
3. Скорости точек АиВ
![]() ,
,![]() .
.
4. Ускорения точек А,В, С![]() ,
,![]() ,
,![]() (найти осе стремительное
(найти осе стремительное![]() и вращательное
и вращательное![]() ускорения
точкиС).
ускорения
точкиС).

Рис.4.3
Решение. Введем неподвижную систему
координатOXYZ с
началом в точкеОконуса 1. Поскольку
конус 1 катится по неподвижному конусу
2 без скольжения, то скорости всех его
точек, лежащих на образующейОА,равны в данный момент времени нулю.
Следовательно, мгновенная ось вращения
конуса 1![]() совпадает с образующейОА.
совпадает с образующейОА.
1. Угол нутации :
![]()
2. Траекторией точки С, с одной
стороны, является окружность, плоскость
которой перпендикулярна мгновенной
оси вращения![]() и центр которой лежит на
и центр которой лежит на![]() ,
с другой стороны,
окружность, плоскость которой
перпендикулярна осиОY оси прецессии
и центр которой лежит на этой оси.
,
с другой стороны,
окружность, плоскость которой
перпендикулярна осиОY оси прецессии
и центр которой лежит на этой оси.
Установив положение мгновенной оси вращения, найдем модуль мгновенной угловой скорости конуса. Поскольку
![]() ,
(4.1)
,
(4.1)
где
![]() кратчайшее расстояние от точкиСдо мгновенной оси
кратчайшее расстояние от точкиСдо мгновенной оси ![]()
![]() ,
то
,
то
![]() 1/с =const. (4.2)
1/с =const. (4.2)
Учитывая заданное направление вектора
![]() ,
,![]() ,
отложим от точкиО вдоль мгновенной
оси
,
отложим от точкиО вдоль мгновенной
оси![]() =ОА вектор
=ОА вектор![]() так, чтобы видеть с его конца вращение
конуса вокруг этой оси
так, чтобы видеть с его конца вращение
конуса вокруг этой оси![]() в направлении, противоположном направлению
движения часовой стрелки (см. рис.4.3).
в направлении, противоположном направлению
движения часовой стрелки (см. рис.4.3).
С другой стороны, поскольку центр С основания конуса 1 движется по окружности, расположенной в горизонтальной плоскости, то
![]() ,
(4.3)
,
(4.3)
где
![]() кратчайшее расстояние от точкиСдо осиОY равно
кратчайшее расстояние от точкиСдо осиОY равно
![]() .
.
3.Отсюда находим модуль угловой скорости
прецессии![]() :
:
![]() 1/с (4.4)
1/с (4.4)
Направление вектора
![]() определяется в зависимости от задания
движения конуса 1, в данном случаепо ходу часовой стрелки, поэтому
определяется в зависимости от задания
движения конуса 1, в данном случаепо ходу часовой стрелки, поэтому
![]() OY( оси прецессии).
OY( оси прецессии).
3.Векторное равенство
![]() , где линии действия всех его составляющих
известны, позволяет определить как
направление векторов всех составляющих
угловых скоростей, так и величину угловой
скорости ротации, а именно : (
, где линии действия всех его составляющих
известны, позволяет определить как
направление векторов всех составляющих
угловых скоростей, так и величину угловой
скорости ротации, а именно : (![]() );
линией действия вектора
);
линией действия вектора![]() является мгновенная ось вращения
является мгновенная ось вращения![]() ;
линией действия вектора
;
линией действия вектора![]()
OY является ось
прецессииOY, линией действия вектора
OY является ось
прецессииOY, линией действия вектора![]() является ось ротацииO
y(см. рис.4.3). Таким
образом, модуль угловой скорости ротации
равен
является ось ротацииO
y(см. рис.4.3). Таким
образом, модуль угловой скорости ротации
равен
 =const
=const
![]() .
(4.5)
.
(4.5)
4. Угловое ускорение
![]() в случае регулярной прецессии определяется
векторным произведением
в случае регулярной прецессии определяется
векторным произведением![]() ,
т.е. вектор
,
т.е. вектор![]()
OZ,так как с
конца осиOZ поворот
вектора
OZ,так как с
конца осиOZ поворот
вектора![]() к вектору
к вектору![]() кажется по ходу часовой стрелки; модуль
углового ускорения определяется как
кажется по ходу часовой стрелки; модуль
углового ускорения определяется как
![]() рад/с2 . (4.6)
рад/с2 . (4.6)
5. Скорости точек конуса 1:
Скорость точки А ![]() ,
так как в данный момент времени эта
точка принадлежит мгновенной оси
вращения конуса 1.
,
так как в данный момент времени эта
точка принадлежит мгновенной оси
вращения конуса 1.
Скорость точки В
![]() ,
где
,
где![]() ,
,
![]() м/с и вектор
м/с и вектор![]() .
.
6. Ускорение какой-либо точки конуса 1 определим как геометрическую сумму осестремительного и вращательного ускорений.
Для точки А конуса 1

где
![]() .
.
Вектор
![]() направлен перпендикулярно плоскости,
в которой лежат векторы
направлен перпендикулярно плоскости,
в которой лежат векторы![]() и
и![]() ,
т.е. перпендикулярноОА в сторону
,
т.е. перпендикулярноОА в сторону
![]() .
.
Таким образом,
![]()
![]()
![]()
Для точки В конуса1
![]()
![]()
Вектор
![]() направлен от точкиBк мгновенной оси вращения конуса 1 (см.
рис.4 3).
направлен от точкиBк мгновенной оси вращения конуса 1 (см.
рис.4 3).
Вектор
![]() перпендикулярен плоскости, в которой
лежат векторы
перпендикулярен плоскости, в которой
лежат векторы![]() и
и![]() ,
принадлежит плоскостиОXY,
т.е. направлен перпендикулярноОB
в сторону
,
принадлежит плоскостиОXY,
т.е. направлен перпендикулярноОB
в сторону ![]() .
.
![]() где
где![]() .
.
Полное ускорение точки B
найдем как диагональ прямоугольника,
построенного на векторах![]() ,
,![]() :
:
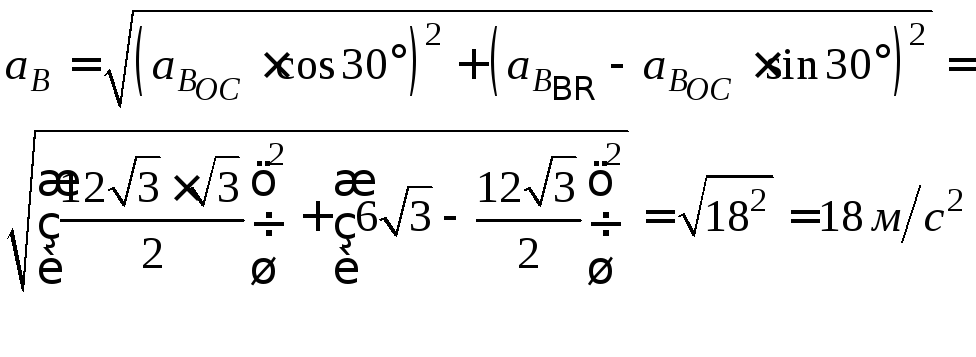 .
.
Для точки С конуса1
а)
![]() EMBED Equation.DSMT4
EMBED Equation.DSMT4![]()
![]()
Вектор
![]() направлен от точкиСк мгновенной
оси вращения
направлен от точкиСк мгновенной
оси вращения
кoнуса 1.
Вектор
![]() перпендикулярен плоскости, в которой
лежат векторы
перпендикулярен плоскости, в которой
лежат векторы![]() и
и![]() ,
принадлежит плоскостиОXY,
т.е. направлен перпендикулярноОС в
сторону
,
принадлежит плоскостиОXY,
т.е. направлен перпендикулярноОС в
сторону ![]() (см.
рис.4.3).
(см.
рис.4.3).
б)

Таким образом
![]() =
=![]()
![]() м/с2
м/с2
Ответ: 1. Угол нутации=/2;
угловая скорость нутации![]() =0;
=0;
прецессии
![]() =
=![]() 1/с;
ротации
1/с;
ротации![]() = 31/с; мгновенная
угловая скорость
= 31/с; мгновенная
угловая скорость![]() =
2
=
2![]() 1/с.
1/с.
2. Угловое ускорение конуса
![]() =3
=3![]() 1/с2.
1/с2.
3. Скорости точек АиВ
![]() = 0;
= 0;![]() =6[ м/с ].
=6[ м/с ].
4. Ускорения точек А,В, С![]() =6
=6![]() ;
;![]() =18;
=18;![]() =
3
=
3![]() [
м/c2];
[
м/c2];
осестремительное ускорение точки
С![]() =
6
=
6![]() м/с2;
м/с2;
вращательное ускорение точки С![]() =
9 м/с2.
=
9 м/с2.
