
MathCad_Дятко_Кишкурно
.pdf
|
Первый способ использует функцию line( X ,Y ) – вектор из двух |
|||||||||||||
элементов |
a, b |
– |
коэффициентов уравнения |
линейной регрессии |
||||||||||
y( x) |
a bx . |
|
|
|
|
|
|
|
|
|
|
|||
|
Во втором способе для определения коэффициента a использует- |
|||||||||||||
ся функция |
intercept ( X , Y ), |
а для вычисления коэффициента b |
||||||||||||
функция slope( X , Y ) . |
|
|
|
|
|
|
|
|||||||
|
Аргументами этих функций являются: |
|
|
|
||||||||||
|
|
X |
x1 , x2 , , |
xn |
T |
|
|
|
|
|
|
|||
|
|
– вектор действительных данных аргумен- |
||||||||||||
та; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 , y2 , |
|
T |
|
|
|
|
|
y(xi ) ) |
|||
|
Y |
, yn |
– вектор действительных данных ( yi |
|||||||||||
того же размера; |
|
|
|
|
|
|
|
|
|
|||||
|
Ниже приводится пример применения этих функций для построе- |
|||||||||||||
ния линейной регрессии. |
|
|
|
|
|
|
|
|||||||
X |
|
( 0 1 |
2 |
3 |
4 5 6 )T |
Y |
( 4.1 |
2.4 |
3 4.3 3.6 5.2 5.9 )T |
|||||
a |
|
|
line(X |
Y) |
|
|
|
a |
|
2.829 |
|
|||
b |
|
|
|
|
|
b |
|
0.414 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
y(x) |
|
a |
b x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
0.1 |
|
|
x |
X0 |
X0 |
x |
Xlast(X) |
|
x |
Xlast(X) |
|
|
|
|
|
|
|
|
|
|
x |
X0 X0 |
|
|||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(x) |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
X x |
|
|
|
|
Коэффициенты a и b можно вычислить и так:
51

a |
intercept(X Y) |
a 2.829 |
b |
slope(X Y) |
b 0.414 |
3.5.2.Регрессия общего вида
Ксожалению, линейная функция далеко не во всех случаях подходит для описания зависимости данных. При более сложных зависимостях между данными приходится использовать уравнение регрессии в виде линейной комбинации известных функций.
y( x) a0 f0( x) a1 f1( x) ... an fn ( x) ,
где коэффициенты a0 ,a1 ,...,an подлежат определению.
Неизвестные коэффициенты можно определить использованием встроенной функции linfit( X, Y , F ).
Аргументы функции:
 X x1 , x2 , , xn T – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
X x1 , x2 , , xn T – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
Y |
y , y |
|
, , y |
T – вектор действительных данных ( y |
|
y(x |
|
) |
|
1 |
2 |
|
n |
i |
|
i |
|
того же размера;
F – функция, представляющая собой вектор, элементами которого являются функции, которые нужно объединить в виде линейной
комбинации, т. е. |
F |
|
f |
0 |
( x), f |
1 |
( x), , f |
n |
( x) |
T . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
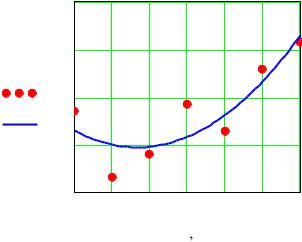
Ниже |
приведен |
|
пример |
построения |
уравнения |
регрессии вида |
|||||||||||||||
y( x) |
a |
0 |
a x |
a |
2 |
x2 |
|
a |
3 |
x3 по набору данных, записанных в вектора |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X и Y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
( 0 |
1 |
2 |
3 |
4 |
5 |
|
6 )T |
|
Y |
( 4.1 |
|
2.4 |
3 |
4.3 |
3.6 5.2 5.9 )T |
|||||
F(x) |
|
1 |
x |
2 T |
|
|
|
|
|
|
A |
linfit(X |
Y |
F) |
|
||||||
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
AT |
|
( 3.602 |
|
0.514 |
0.155 ) |
y (x) |
|
A F(x) |
|
|||||||||||
|
x |
|
0.1 |
|
|
|
x |
|
X0 |
X0 |
x Xlast(X) |
|
|
||||||||
52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
X0 |
X0 |
x |
|
Xlast(X) |
|
7 |
|
|
|
|
|
|
|
|
5.75 |
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
y(x) |
4.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.25 |
|
|
|
|
|
|
|
|
2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
X x |
|
|
|
|
3.6. Математическая статистика
Пакет Mathcad имеет развитый аппарат работы с задачами математической статистики. С одной стороны, имеется большое количество встроенных специальных функций, позволяющих рассчитывать плотности вероятности и другие основные характеристики основных законов распределения случайных величин. Наряду с этим, в Mathcad запрограммировано соответствующее количество генераторов псевдослучайных чисел для каждого закона распределения, что позволяет эффективно проводить моделирование методами Монте-Карло. Имеется возможность строить гистограммы и рассчитывать статистические характеристики выборок случайных чисел и случайных процессов, таких как средние, дисперсии, корреляции и т. п. При этом случайные последовательности могут как создаваться генераторами случайных чисел, так и вводиться пользователем из файлов.
3.6.1. Случайные величины
Для моделирования различных физических, экономических и прочих эффектов широко распространены методы, называемые методами Монте-Карло. Их основная идея состоит в создании определенной последовательности случайных чисел, моделирующей тот или иной эффект, например шум в физическом эксперименте, случайную динамику биржевых индексов и т. п. Для этих целей в Mathcad встроен ряд генераторов псевдослучайных чисел. Такие генераторы реализованы в виде встроенных функций, создающих
53

выборку псевдослучайных данных с соответствующим законом распределения.
Рассмотрим некоторые из этих функций:
 rnorm(N , m , у) – возвращает вектор N случайных чисел,
rnorm(N , m , у) – возвращает вектор N случайных чисел,
имеющих нормальное распределение с математическим ожиданием m и среднеквадратичным отклонением у (квадратный корень из дисперсии).
 runif(N , a , b) – возвращает вектор N случайных чисел, имеющих равномерное распределение на отрезке [a , b] , a b .
runif(N , a , b) – возвращает вектор N случайных чисел, имеющих равномерное распределение на отрезке [a , b] , a b .
 rnd( x) – возвращает равномерно распределенное случайное число на отрезке [0, x] . Эквивалент runif(1, 0, x) .
rnd( x) – возвращает равномерно распределенное случайное число на отрезке [0, x] . Эквивалент runif(1, 0, x) .
3.6.2.Числовые характеристики случайных величин
ВMathcad имеется ряд встроенных функций для расчетов числовых статистических характеристик случайных данных.
Пусть X x1 , x2 , , xn T – вектор действительных случайных
данных (выборка). Тогда для него могут быть вычислены следующие числовые характеристики:
|
1 |
|
n |
|
mean(X ) – выборочное среднее значение, mean(X ) |
|
|
xi ; |
|
n i |
||||
|
1 |
|||
 median(X ) – выборочная медиана (median) – значение аргумен-
median(X ) – выборочная медиана (median) – значение аргумен-
та, которое делит гистограмму (см. ниже) плотности вероятностей на две равные части;
 var( X ) – выборочная дисперсия (variance),
var( X ) – выборочная дисперсия (variance),
|
1 |
|
n |
|
mean(X ) 2 |
; |
|
var( X ) |
|
|
x |
i |
|||
n i |
|||||||
|
1 |
|
|
||||
|
|
|
|
||||
 stdev(X ) – среднеквадратичное (или «стандартное») отклонение
stdev(X ) – среднеквадратичное (или «стандартное») отклонение
(standarddeviation), stdev(X ) 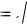 var( X ) ;
var( X ) ;
 max(X ) , min(X ) – максимальное и минимальное значения выборки;
max(X ) , min(X ) – максимальное и минимальное значения выборки;
 mode(X) – наиболее часто встречающееся значение выборки;
mode(X) – наиболее часто встречающееся значение выборки;
54

3.6.3. Построение гистограммы
Гистограммой называется график, аппроксимирующий по случайным данным X x1 , x2 , , xn T плотность их распределения.
При построении гистограммы область значений случайной величины[a, b] разбивается на некоторое количество N сегментов, а затем
подсчитывается процент попадания данных в каждый сегмент. Для построения гистограмм в Mathcad имеется несколько встроенных функций. Рассмотрим наиболее удобную из них, функцию histogram(N , X ) . Функция возвращает матрицу, состоящую из двух
столбцов. Первый столбец содержит сегменты разбиения данных, а второй – число попадающих в них данных. Рассматриваемая функция рассчитывает гистограмму для сегментов равной длины.
Приведем пример, демонстрирующий применение рассмотренных функций в задаче статистического анализа выборки случайных данных.
Сформулируем следующую задачу:
получить выборку из 100 случайных чисел, имеющих нормальный закон распределения вероятностей со средним значением 5 и дисперсией 2;
определить числовые характеристики выборки; построить гистограмму.
Ниже приведен пример решения поставленной задачи в пакете
Mathcad.
|
|
|
|
|
|
|
|
N |
100 |
m 5 |
D 2 |
|
D |
||
X |
rnorm(N m |
) |
|
|
|
||
m_X |
|
mean(X) |
m_X |
4.787 |
|
|
|
var_X |
var(X) |
var_X |
1.91 |
|
|
||
_X |
|
stdev(X) |
_X |
1.382 |
|
|
|
max_X |
|
max(X) |
max_X |
9.311 |
|
|
|
min_X |
min(X) |
min_X |
0.898 |
|
|
||
median_X |
median(X) |
median_X 4.901 |
|||||
55

|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H 1 |
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
4 |
6 |
|
|
|
|
8 |
|
|
|
10 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H 0 |
|
|
|
|
|
|
|||||||||
Для отображения графика в виде гистограммы необходимо: построить двухмерный график;
перейти в режим форматирования и выбрать вкладку Traces (Линии);
раскрыть список Type (Тип) и выбрать тип диаграммы bar.
Если на гистограмме необходимо отображать не число, а частоту попаданий данных в соответствующие интервалы, то второй столбец матрицы H необходимо пронумеровать, как показано ниже.
Y
H 1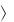
N
0.3 |
|
|
|
|
|
|
0.24 |
|
|
|
|
|
|
0.18 |
|
|
|
|
|
|
Y |
|
|
|
|
|
|
0.12 |
|
|
|
|
|
|
0.06 |
|
|
|
|
|
|
0 |
0 |
2 |
4 |
6 |
8 |
10 |
|
|
|
|
H 0 |
|
|
3.7. Поиск экстремума функции
Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значе-
56
ния) в некоторой области определения ее аргументов. Ограничения |
||||||||||
значений аргументов, задающих эту область, как и прочие дополни- |
||||||||||
тельные условия, должны быть определены в виде системы нера- |
||||||||||
венств и (или) уравнений. В таком случае говорят о задаче на услов- |
||||||||||
ный экстремум. Для решения задач поиска максимума и минимума в |
||||||||||
Mathcad имеются встроенные функции Minimize и Maximize. С |
||||||||||
помощью этих функций решается задача поиска локальных экстре- |
||||||||||
мумов функции. |
|
|
|
|
|
|
|
|
|
|
3.7.1. Экстремум функции одной переменной |
|
|
||||||||
|
Для поиска экстремума функции одной переменной рассматри- |
|||||||||
ваемые встроенные функции имеют следующий синтаксис: |
||||||||||
Minimize( f , x) и Maximize( f , x) . Здесь |
f – имя функции, для кото- |
|||||||||
рой находится экстремум, а x – имя переменной, по которой выполня- |
||||||||||
ется поиск. |
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим следующий пример. Пусть требуется найти все ло- |
|||||||||
кальные экстремумы |
функции |
f ( x) |
x4 |
5x3 |
x |
10 на отрезке |
||||
x |
[ 5, 5] . |
|
|
|
|
|
|
|
|
|
|
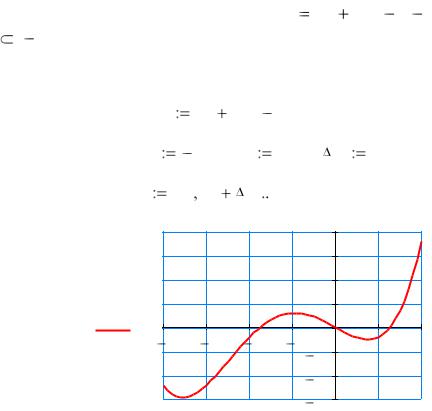
Построим на указанном отрезке график функции |
f ( x) |
||||||||
|
f (x) |
|
x4 |
5x3 |
10x |
|
|
|
|
|
|
x1 |
|
4 |
x2 |
|
2 |
x |
0.1 |
|
|
|
x |
x1 x1 |
x |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
f (x) |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
2 |
1 |
10 0 |
1 |
|
2 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |

Из графика видно, что на указанном отрезке функция имеет три локальных экстремума: два локальных минимума и один локальный максимум. Для поиска первого локального минимума укажем, исходя из графика функции, для переменной x некоторое начальное приближение к точке x1_ min и воспользуемся функцией Minimizeкак пока-
зано ниже. Затем вычислим значение функции в найденной точке x1_ min .
x |
4 |
x1_min Minimize(f |
x) |
x1_min |
3.552 |
y1_min |
f (x1_min) |
y1_min |
29.371 |
|
|
Аналогичным образом определяем x _ max , x2 _ min и значения функции в этих точках. Результат показан ниже.
x |
4 |
x1_min Minimize(f x) |
x1_min |
3.552 |
||
y1_min |
f (x1_min) |
y1_min |
29.371 |
|
||
x |
1.5 |
x_max |
Maximize(f x) |
|
x_max |
0.944 |
y_max |
f (x_max) |
y_max |
6.028 |
|
||
x |
1 |
x2_min Minimize(f x) |
|
x2_min |
0.746 |
|
y2_min |
f (x2_min) |
y2_min |
5.074 |
|||
3.7.2. Экстремум функции многих переменных
Для поиска экстремума функции многих переменных y f ( x1 , x2 , , xn )
рассматриваемые встроенные функции имеют следующий синтаксис:
Minimize( f , x1 , x2 , , xn ) и Maximize( f , x1 , x2 , , xn ).
Здесь f – имя функции, для которой находится экстремум, а
x1 , x2 , , xn – имена переменных по которым выполняется поиск. При этом необходимо указать начальное приближение к искомой точке экс-
тремума в виде: |
x |
x0 |
, |
x |
2 |
x0 |
, …, |
x |
n |
x0 |
. Указанное требование в |
|
1 |
1 |
|
|
2 |
|
|
n |
|
||
58 |
|
|
|
|
|
|
|
|
|
|
|
общем случае может оказаться весьма непростой задачей для функции многих переменных.
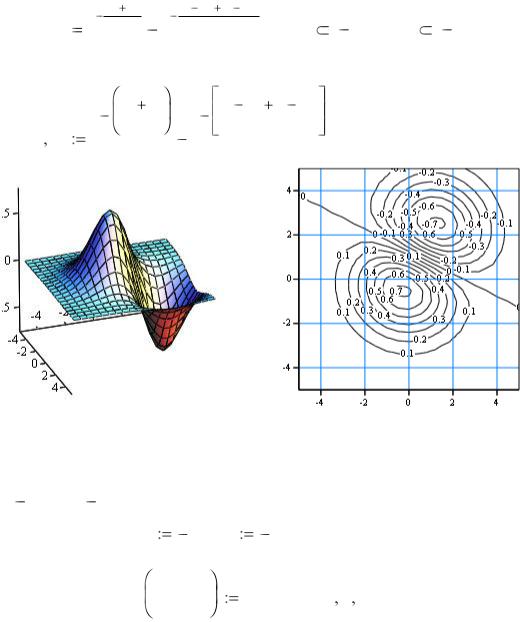
Отдельно рассмотрим вопрос о поиске экстремума функции двух переменных z 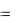 f ( x, y) . В рассматриваемом случае для поиска на-
f ( x, y) . В рассматриваемом случае для поиска на-
чального приближения можно воспользоваться картой линий уровня. Рассмотрим следующий пример. Пусть требуется найти все экстремумы функции
x2 y2 ( x 1)2 ( y 2)2
f ( x, y) e |
5 |
e |
5 |
для x [ 5, 5] |
и y [ 5, 5] |
|
|
|
|
Построим график функции и карту линий уровня.
|
|
x2 y2 |
|
(x 1)2 (y 2)2 |
||
f (x y) |
e |
5 |
|
e |
5 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
f |
|
Используя карту линий уровня, выбираем начальное приближение ( x 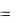 1, y
1, y 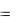 2) для поиска локального максимума и находим его.
2) для поиска локального максимума и находим его.
x |
1 y |
2 |
x_max
Maximize(f x y)
y_max
59

x_max |
0.272 |
|
y_max |
0.543 |
||||
|
|
f (x_max y_max) |
0.73 |
|
|
|||
Аналогично определяем начальное приближение для поиска ло- |
||||||||
кального минимума ( x |
3, |
y |
4) и находим его. |
|
||||
x |
3 |
y |
4 |
|
|
|
|
|
x_min |
Minimize(f |
x y) |
x_min |
1.272 |
||||
y_min |
||||||||
|
|
|
|
|
|
|
||
y_min |
2.543 |
|
f (x_min y_min) |
0.73 |
||||
Рассмотрим еще один пример на условный экстремум. Пусть необходимо найти минимум функции f ( x, y) x 2 y 2 2 при условии, что x y 1.
Поскольку данная функция является квадратичной, то она имеет единственный минимум. Это означает, что в качестве начального приближения для поиска минимума можно взять любое число, например x 0 и y 0 .
Для поиска условного экстремума функции необходимо использовать блок Given, как показано ниже.
x |
0 |
|
|
y |
0 |
|
|
Given |
|
|
|
|
|||
x |
y |
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
||||
|
x_min |
|
Minimize(f |
x y) |
|||
|
y_min |
|
|||||
|
|
|
|
|
|||
x_min |
0.5 |
|
y_min |
0.5 |
|||
f (x_min y_min) |
2.5 |
|
|||||
60
