
MathCad_Дятко_Кишкурно
.pdf
max(A) |
Максимальный элемент в массиве A |
min(A) |
Минимальный элемент в массиве A |
identity(n) |
(n n) – единичная матрица |
diag(v) |
Диагональная матрица, содержащая на диагонали |
|
элементы вектора v |
tr(A) |
Сумма диагональных элементов матрицы A (след |
|
A). Матрица A должна быть квадратной |
Рассмотрим примеры некоторых операций с матрицами и векторами. Для формирования матричных операторов удобно использовать
панель инструментов Matrix. Произведение матриц:
|
1 |
2 |
4 |
|
3 |
2 |
1 |
|
51 |
40 |
47 |
A |
6 |
7 |
9 |
B |
6 |
5 |
9 |
C A B |
C 141 |
110 |
132 |
|
4 |
7 |
8 |
|
9 |
7 |
7 |
|
126 |
99 |
123 |
Произведение матрицы на вектор:
|
1 |
|
|
|
49 |
|
V |
6 |
|
P |
A V P |
129 |
|
|
9 |
|
|
|
118 |
|
Транспонирование матрицы и вектора: |
|
|||||
|
1 |
6 |
4 |
|
|
|
AT |
2 |
7 7 |
VT |
( 1 6 9 ) |
||
|
4 |
9 |
8 |
|
|
|
Вычисление определителя матрицы: |
|
|||||
|
|
|
|
|
|
|
D |
|
A |
|
|
|
D 25 |
Вычисление обратной матрицы: |
|
|||||
31

|
0.28 |
0.48 |
0.4 |
|
1 |
0 |
0 |
S A 1 S |
0.48 |
0.32 |
0.6 |
I A A 1 I |
0 |
1 |
0 |
|
0.56 |
0.04 |
0.2 |
|
0 |
0 |
1 |
Скалярное произведение векторов:
2
W 5 |
P W V P 95 |
7
Сумма элементов вектора:
s |
V |
s 16 |
Выделение из матрицы и второго столбца и второй строки:
|
|
|
2 |
|
|
1 |
|
|
Y A |
1 |
Y |
7 |
Z |
T |
T |
( 6 7 9 ) |
|
|
A |
|
Z |
|||||
|
|
|
7 |
|
|
|
|
|
Число строк и столбцов матрицы: |
|
|
|
|
||||
n |
|
rows(A) |
n 3 |
m |
|
cols(A) |
m 3 |
|
Максимальный и минимальный элемент матрицы:
Bmax max(B) Bmax 9 |
Bmin min(B) Bmin 1 |
Число элементов вектора:
k  length(V) k 3
length(V) k 3
Номер последнего элемента вектора:
m last(V) |
m 2 |
Создание единичной матрицы:
1 |
0 |
I identity(2) I |
|
0 |
1 |
32

Создание диагональной матрицы из элементов вектора:
1 0 0
T diag(V) T |
0 6 0 |
0 0 9
Вычисление следа (сумы диагональных элементов) квадратной матрицы:
Sp 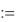 tr(A) Sp 16
tr(A) Sp 16
Рассмотрим построение графика функции, когда ее рассчитанные значения и значения ее аргумента предварительно записаны в массивы.
f (x) |
3x e x |
|
|
|
|
|
|
|
x1 |
0 |
x2 |
5 |
x |
0.1 |
N |
x2 |
x1 |
|
x |
|||||||
|
|
|
|
|
|
|
|
|
i 0 N Xi |
x1 i x Yi |
f Xi |
|
|
||||
|
1.5 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
2 |
3 |
4 |
|
5 |
|
|
|
|
|
X |
|
|
|
Для выполнения поэлементных операций над элементами векторов или матриц в пакете Mathcad существует оператор векторизации, который предписывает Mathcad применять операторы и функции к каждому элементу массива поочередно. Так если V – вектор, то sin(V) – недопустимое выражение. Но если использовать оператор векторизации, Mathcad вычисляет синус каждого элемента вектора V, а результат – новый вектор, чьи элементы – синусы элементов V.
Для применения оператора векторизации к некоторому выражению необходимо:
33

установить в нужном месте документа шаблон оператора векторизации (нажать комбинацию клавиш <Ctr>+<–> или воспользовать-
ся палитрой символов 
 ); заполнить шаблон необходимым выражением. Например:
); заполнить шаблон необходимым выражением. Например:
|
0.841 |
0.909 |
0.757 |
|
0.54 |
sin(A) |
0.279 |
0.657 |
0.412 |
cos(V) |
0.96 |
|
0.757 |
0.657 |
0.989 |
|
0.911 |
3.2.Решение уравнений и систем уравнений
3.2.1.Системы линейных уравнений
Рассмотрим систему линейных уравнений:
a11 x1 |
a12 x2 a1n |
b1 |
a21 x1 |
a22 x2 a2n |
b2 , |
|
|
|
an1 x1 |
an2 x2 ann |
bn |
Запишем ее в матричном виде:
AX B ,
|
|
a11 |
a12 |
a1n |
|
|
где A |
a21 |
a22 |
a2n |
– квадратная матрица размером n×n |
||
|
|
|
|
|
|
|
|
|
an1 an2 |
ann |
|
||
|
b1 |
|
|
|
|
|
B |
b2 |
|
– вектор размером n×1 |
|||
bn
34

x1
X |
x2 |
– вектор неизвестных размером n×1 |
xn
Из курса линейной алгебры известно, что решение рассматриваемой системы уравнений имеет вид:
X A 1 B
Ниже приведен пример решения системы линейных уравнений:
2x |
3 y |
z |
5 |
x |
2 y |
3z |
6 |
3x |
y |
2z |
1 |
в пакете Mathcad.
|
2 |
3 |
1 |
|
5 |
x |
|
A |
1 |
2 |
3 |
B |
6 |
y |
A 1 B |
|
3 |
1 |
2 |
|
1 |
z |
|
|
x |
|
|
1 |
|
|
|
X |
y |
|
X |
2 |
x 1 |
y |
2 z 3 |
|
z |
|
|
3 |
|
|
|
В Mathcad имеется встроенная функция lsolve(A,B), которая служит для решения системы линейных уравнений. Далее приведен пример решения рассматриваемой системы с помощью этой функции.
1 X  lsolve(A B) X 2 3
lsolve(A B) X 2 3
3.2.2. Одно уравнение с одним неизвестным |
|
|
Для решения одного уравнения с одним неизвестным f ( x) |
0 в |
|
пакете Mathcad используются функции |
root( f ( x), x) |
и |
|
|
35 |
root( f ( x), x,a,b) , где f ( x) – функция, определенная где-либо в рабо-
чем документе, или выражение, которое возвращает скалярное значение, x – имя переменной, относительно которой ищется решение уравнения.
Функция root( f ( x), x) требует дополнительного задания началь-
ного значения (guess value) переменной x. Для этого нужно просто предварительно присвоить x некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение на-
чального значения требует априорной информации о примерной локализации корня.
Если функция f ( x) имеет несколько корней, то найденное значе-
ние корня будет зависеть от начального приближения для переменной x. Будет найдено такое значение корня, в окрестности которого задано начальное приближение.
Рассмотрим пример. Пусть необходимо найти все корни уравнения e xcos( x) 0,5 на отрезке  1,5; 1,5 .
1,5; 1,5 .
Ниже приведен пример решения этого уравнения с применением функции root( f ( x), x) . Для локализации корней используется по-
строение графика функции на заданном интервале.
f (x) |
e x cos(x) |
0.5 |
|
|
|
|
x1 |
1.5 |
x2 |
1.5 |
x |
0.1 |
|
x |
x1 x1 |
x |
x2 |
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
1 |
|
|
|
f (x) |
|
|
0.5 |
|
|
|
|
2 |
1 |
0 |
|
1 |
2 |
|
|
|
0.5 |
|
|
|
|
|
|
x |
|
|
|
36

x |
|
2 - начальное приближение для первого корня |
||||
x1 |
root(f (x) |
x) |
x1 |
1.454 |
- найден первый корень |
|
x |
1 |
- начальное приближение для второго корня |
||||
x2 |
root(f (x) |
x) |
x2 |
0.54 |
- найден второй корень |
|
Иногда удобнее задавать не начальное приближение к корню, а интервал a, b , внутри которого корень заведомо находится. В этом
случае следует использовать функцию root( f ( x), x,a,b) с четырьмя
аргументами, а присваивать начальное значение x не нужно, как показано ниже.
x1 |
root(f (x) |
x |
|
2 |
1) x1 |
1.454 |
x2 |
root(f (x) |
x |
0 |
1) |
x2 |
0.54 |
При использовании функции root( f ( x), x,a,b) необходимо помнить следующее:
внутри интервала a, b не должно находиться более одного корня. Иначе будет заранее неизвестно, какой именно из корней найден;
значения функций f (a)и f (b) должны иметь разный знак, иначе
будет выдано сообщение об ошибке.
Для нахождения корней полинома, т. е. для решения уравнения
a |
n |
xn |
|
a |
n |
1 |
xn |
1 ... |
a x a |
0 |
0 |
используется |
|
функция |
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
polyroots(V ) , |
где |
|
V |
– |
|
вектор |
коэффициентов |
полинома. |
||||||||||||
V T |
a |
0 |
,a ,...,a |
n 1 |
,a |
n |
. Функция возвращает вектор, элементами кото- |
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
рого являются корни полинома. |
|
|
|
|
|
|
|
|||||||||||||
|
|
Пример. Найти все корни уравнения x3 |
2x2 |
x |
2 |
0 |
||||||||||||||
|
|
|
|
|
V |
|
( |
2 |
1 |
2 |
1 )T |
- вектор коэффициентов |
|
|
|
|||||
|
|
|
|
|
X |
|
polyroots(V) |
XT |
|
( 2 |
1 1 ) |
- вектор корней |
||||||||
|
|
Пример. Найти все корни уравнения x3 |
10x |
2 |
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |

V |
( 2 10 |
0 1 )T |
- вектор коэффициентов |
|
X |
polyroots(V) |
|
|
|
XT |
( 3.258 |
0.201 |
3.057 ) |
- вектор корней |
3.2.3. Системы нелинейных уравнений
Пусть необходимо решить систему уравнений
f1 (x1 , x2 ,..., xn ) |
0 |
f 2 (x1 , x2 ,..., xn ) |
0 |
........................ |
|
f n (x1 , x2 ,..., xn ) |
0 |
Процедура решения в пакете Mathcad имеет следующий вид: задаются начальные значения для всех переменных системы:
x1 : x10 x2 : x20
.............
xn : xn0
Given – ключевое слово; записываются уравнения системы:
f1 (x1 , x2 ,..., xn ) |
0 |
f 2 (x1 , x2 ,..., xn ) |
0 |
........................ |
|
f n (x1 , x2 ,..., xn ) |
0 |
 находится решение системы уравнений в виде вектора значений соответствующих переменных.
находится решение системы уравнений в виде вектора значений соответствующих переменных.
V : Find (x1 , x2 ,..., xn )
Здесь V : Find( x1, x2 ,...,xn ) – функция, которая возвращает ре-
шение системы уравнений в виде вектора значений соответствующих переменных, если оно существует.
38
При записи системы уравнений, после ключевого слова Given, |
|||||||||||||
при необходимости можно указывать ограничения на возможные зна- |
|||||||||||||
чения переменных, используя символы |
, |
, |
и . |
||||||||||
Замечание. При записи уравнений внутри блока Given…Find |
|||||||||||||
знак равенства следует вводить нажатием комбинаций клавиш |
|||||||||||||
<Ctrl>+<=> или использовать символ Equal to (логическое равенство) |
|||||||||||||
из палитры символов Boolean (Булево). |
|
|
|
|
|
||||||||
Если система уравнений является нелинейной, то найденное ре- |
|||||||||||||
шение может быть не единственным и зависеть от начальных значе- |
|||||||||||||
ний переменных. |
|
|
|
|
|
|
|
|
|
|
|||
Пример. Решить систему уравнений для x |
4, 4 : |
||||||||||||
y |
x 2 |
5 |
0 |
|
|
|
|
|
|
|
|
|
|
y |
x 2 |
2x |
4 |
0 |
|
|
|
|
|
|
|
|
|
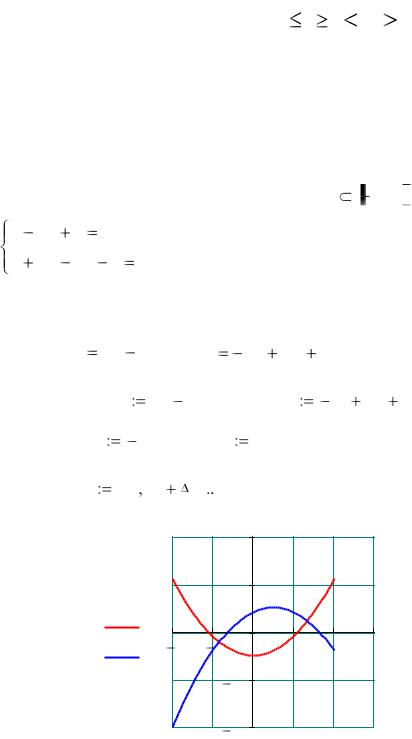
Для поиска начальных приближений для переменных x и y вы- |
|||||||||||||
ражаем из каждого уравнения |
y |
как функцию |
x и строим графики |
||||||||||
функций y1( x) |
|
x 2 |
5 и y2( x) |
x2 |
2x |
4 . |
|
|
|||||
|
|
|
y1 (x) |
x2 |
5 |
|
y2 (x) |
x2 |
2x |
4 |
|||
|
|
|
x1 |
|
4 |
|
x2 |
4 |
|
|
|
|
|
|
|
|
x |
x1 x1 |
x |
x2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
y1(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
y2(x) |
4 |
2 |
0 |
|
2 |
4 |
6 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
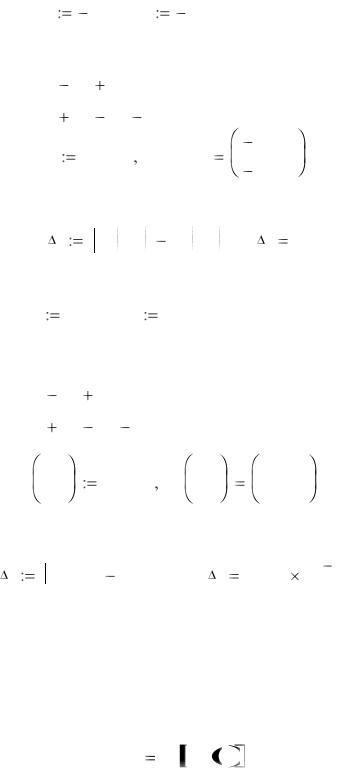
Находим первое решение:
x |
2 |
|
|
y |
1 |
|
Given |
|
|
|
|
|
|
y |
x2 |
5 |
|
0 |
|
|
|
|
|
||||
|
|
|
||||
y |
x2 |
2x |
4 |
|
0 |
|
|
||||||
|
||||||
|
1.679 |
V Find(x y) |
V |
|
2.179 |
Проверка найденного решения:
y1 V0 y2 V0 |
0 |
Находим второе решение:
x |
2 |
|
|
y |
1 |
|
|
Given |
|
|
|
|
|
|
|
y |
x2 |
5 |
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
||||
y |
x2 |
2x |
4 |
|
0 |
|
|
|
|
||||||
|
|
||||||
|
x0 |
|
|
|
|
x0 |
2.679 |
|
|
Find(x y) |
|
||||
|
y0 |
|
|
|
|
y0 |
2.179 |
Проверка найденного решения:
y1 (x0) |
y2 (x0) |
|
10 |
15 |
1.776 |
3.3.Дифференциальные уравнения и системы
3.3.1.Дифференциальные уравнения первого порядка
Рассмотрим обыкновенное дифференциальное уравнение (ОДУ) первого порядка
dy |
f x, y x |
|
|
||
dx |
||
|
40
