
1 / Алгебра и геометрия / Методички / pdf / Геометрия / Geometry
.pdf
Взаимное расположение двух прямых в пространстве
Пусть прямые l1 и l2 заданы каноническими уравнениями
l |
: |
|
x − x1 |
= |
|
y − y1 |
= |
z − z1 |
|
|||
|
|
|
|
|
||||||||
1 |
|
m1 |
|
|
|
n1 |
|
|
|
p1 |
||
|
|
|
|
|
|
|
|
|
||||
l2 |
: |
|
x − x2 |
= |
y − y2 |
= |
z − z2 |
|||||
|
|
|
p2 |
|||||||||
|
|
|
m2 |
|
|
|
n2 |
|
|
|
||
Обозначим b = M1M 2 = (х2-x1,y2-у1,z2-z1), a1 =(m1,n1,р), a2 = (m2,n2,р2).
1) |
если прямые совпадают, то все три вектора a1 , a2 ,b |
||
коллинеарны. |
|
a1 и a2 |
|
2) |
если прямые параллельны и не совпадают, то вектора |
||
коллинеарны, а вектор b им не коллинеарен. |
два из векторов a1 , |
||
3) |
если пряже пересекаются, то никакие |
||
a2 ,b не коллинеарны, и все три вектора компланарны. |
b , a1 , a2 |
||
4) |
ecли прямые скрещиваются, то |
векторы |
|
некомпланарны.
Отметим, что условия параллельности и перпендикулярности, прямых l1 и l2 равносильны условиям коллинеарности и ортогональности их направляющих векторов a1 и a2 .
Следовательно,
m1 = n1 = p1 m2 n2 p2
- необходимое и достаточное условие параллельности двух прямых.
m1m2 + n1n2 + p1p2 = 0
31
- необходимое и достаточное условие перпендикулярности двух прямых.
Если прямые l1 и l2 пересекаются, то величина угла φ между ними равно либо (a1 ^, a2 ) либо (-a1 ^,a2 ). Следовательно,
cosϕ = |
| m1m2 + n1n2 + p1 p2 | |
|||||
m2 |
+ n2 |
+ p2 |
m2 |
+ n2 |
+ p2 |
|
|
1 |
1 |
1 |
2 |
2 |
2 |
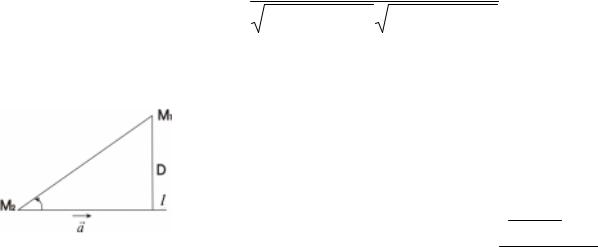
Расстояние от точки до прямой в пространстве
Расстояние d от точки M1(x1,у1,z1) до данной
прямой |
l : |
x − x0 |
= |
y − y0 |
= |
z − z0 |
, проходящей |
|
m |
n |
p |
||||||
|
|
|
|
|
через точку M0(х0,у0,z0) с направляющим вектором a = (m, n, p) определяется так d = | M 0|Mar1|×ar| .
Уравнение плоскости, проходящей через две заданные прямые
Пусть плоскость α проходят через прямые l1 и l2, заданные соответственно уравнениями:
l : |
x − x1 |
= |
y − y1 |
= |
z − z1 |
, l |
2 |
: |
x − x2 |
= |
|
y − y2 |
= |
z − z2 |
(2) |
||
|
|
|
|
|
|
|
|||||||||||
1 |
m1 |
|
n1 |
|
p1 |
|
|
|
m2 |
n2 |
|
p2 |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
Обозначим |
М2(x2,y2,z2), |
a1 =(m1,n1,р1), |
a2 =(m2,n2,p2) |
и М(х,у,z) |
|||||||||||||
произвольная точка плоскости α |
|
|
|
|
|
|
|
|
|
||||||||
Тогда |
|
|
|
x − x2 |
y − y2 |
z − z2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
m1 |
|
n1 |
|
p1 |
|
= 0 |
|
|
|
|||
|
|
|
|
|
m2 |
|
n2 |
|
p2 |
|
|
|
|
|
|||
- уравнение плоскости, проходящей через две прямые.
32

Расстояние между скрещивающимися прямыми
Пусть прямые l1 и l2, заданные уравнениями вида (2), являются скрещивающимися. Тогда расстоянием d между ними называется длина перпендикуляра, проведенного из одно прямой на другую. Заметим, что искомое расстояние равно отрезку перпендикуляра, закаченного между плоскостями α1 и α2, где плоскости α1 и α2 одновременно параллельны векторам a1 и a2 , и проходят
соответственно через прямые l1 и l2 Тогда
|
| ( |
|
,ar |
,ar ) | |
|
d = |
M M |
||||
2 |
1 |
1 |
2 |
||
|
|
| ar1 ×ar2 |
| |
||
Взаимное расположение прямой и плоскости
Пусть прямая l и плоскость α заданы соответственно уравнениями
l : x −mx0 = y −n y0 = z −pz0 , α: Ax + By + Cz + D
= 0.
1) прямая l лежит в плоскости α, если
Am + Bn + Ср = 0, Аx0 + Ву0 + Cz0 + D = 0.
2) прямая l параллельна плоскости α, если
Am + Bn + Ср = О, Аx0 + Ву0 + Cz0 + D ≠ 0.
3) прямая l пересекает плоскость α если
Am + Вn + Ср ≠ 0.
33

Угол между прямой и плоскостью
Углом между прямой l и плоскостью α называется угол φ,
образованный прямой l и ее проекцией l1 на плоскость α
Тогда 0 ≤ϕ ≤π / 2 и
|
r |
|
sinϕ = |
|rN ar| |
. |
|
| N | | a | |
|
КРИВЫЕ ВТОРОГО ПОРЯДКА
Парабола
Определение: Параболой называется геометрическое место точек плоскости, равноудаленных от некоторой точки, называемой
фокусом параболы и некоторой прямой, |
называемой директрисой |
параболы. |
|
Уравнение параболы принятo записывать в следующем виде: |
|
y2 = 2px , p>0 |
(1) |
- каноническое уравнение параболы.
Свойства параболы непосредственно следуют из свойств уравнения:
1.Абсцисса любой точки параболы неотрицательна
2.Парабола проходит через начало координат.
3.Парабола симметрична относительно оси абсцисс.
4.При неограниченном возрастании абсциссы x ордината у возрастает по абсолютной величине.
34

Точка F( 2p ;0) называется фокусом параболы, прямая x = −2p
- директрисой.
Величина р называется фокальным параметром или просто
параметром параболы.
Эллипс
Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2а (а>0), большая, чем расстояние между
фокусами.
Для составления уравнение эллипса выберем прямоугольную декартову систему координат так, чтобы ось ОХ
проходила через фокусы F1 и F2, а начало координат — точка О находилась в середине отрезка F1F2.
Обозначим F1F2 = 2с. Тогда F1(-с,0), F2(c,0). Пусть М(х,у) – произвольная точка эллипса. Тогда MF1+ MF2= 2а, а>с.
Так как a > c a2 −c2 = b2 > 0, и уравнение принимает вид:
x2 |
+ |
y2 |
=1. |
(2) |
|
a2 |
b2 |
||||
|
|
|
Пусть координаты точки М1(х1,у1)удовлетворяют уравнению (2).
Обозначим r1 = F1M1, r2 = F2M2 — фокальные радиусы точек М1
М2. Тогда r = a + |
c |
x , r |
= a − |
c |
x |
|
, значит, r1+r2=2a. |
|
|
|
|||||
1 |
a 3 2 |
|
a |
2 |
|
||
Теперь по свойствам уравнения (2) исследуем геометрические свойства эллипса.
1.Оси ОХ и ОУ являются осями симметрии эллипса. Следовательно, эллипс достаточно исследовать только в первой координатной четверти.
2.Эллипс пересекает координатные оси в точках А1(-а,0), А2(а,0),
В1(0,b), В2(0,-b), называемых вершинами эллипса.
35

3.Эллипс расположен в прямоугольнике, ограниченном прямыми х=±а, у =±b.
4.Из уравнений следует, что при возрастании х от 0 до а в первой координатной четверти, у убывает от b до 0.
По полученным свойствам строим эллипс Отрезок А1А2 и его длина 2а называются большой осью эллипса, а отрезок B1B2 и его длина 2b называются малой осью эллипса. Отрезок ОА1 с длиной а и отрезок ОВ1 с длиной b называются соответственно большой и малой полуосями эллипса. Длина отрезка F1F2=2с называется фокусным расстоянием, начало координат — центр эллипса.
Если а=b, то получаем каноническое уравнение окружности
|
|
|
|
|
|
|
|
x2 + y2 = a2 |
||
|
|
|
|
Уравнения х = acost, у = bsint - |
||||||
|
|
|
|
параметрические уравнения эллипса. |
||||||
Определение. Эксцентриситетом эллипса называется число |
||||||||||
|
|
|
|
|
ε = |
c |
|
|
|
|
|
|
|
|
|
a |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
Так как с<а, то 0<c<1. Заметим, что у окружности оба фокуса |
||||||||||
совпадают, поэтому с = 0 и ε = 0. |
b 2 |
|||||||||
ε |
2 |
|
c2 |
a2 −b2 |
||||||
|
= |
|
= |
|
=1− |
|
. |
|||
|
a2 |
a2 |
a |
|||||||
Следовательно, эксцентриситет характеризует форму эллипса. Используя понятия эксцентриситета, можно выразить фокальные
радиусы произвольной точки M(x,у) эллипса:
r1=а+εх, r2=а—εх
Гипербола
Определение. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами гиперболы, есть величина
36

постоянная, равная 2а, а>0, меньшая чем расстояние между фокусами. Выберем декартову прямо-угольную систему координат ОХY
так, как показано на рисунке. Тогда F1F2=2с, F1(—с,0), F2(c,0).
Для произвольной точки М(х,у), принадлежащей гиперболе,
имеем МF1—MF2=±2а, а<с.
Обозначим с2-а2=b2, тогда каноническое уравнение гипрболы
имеет вид:
x2 |
− |
y2 |
=1 |
(3) |
|
a2 |
b2 |
||||
|
|
|
По свойствам уравнения (3) исследуем свойства гиперболы:
1. Координатные оси являются осями симметрии гиперболы. Поэтому гиперболу достаточно исследовать только в первой координатной четверти.
2.Если у = 0, то x = ±а. Если х = 0, то уравнение (3) решений
не имеет. Значит, гипербола пересекает только ось ОХ в точках А1(—
а,0), А2(а,0), называемых вершинами гиперболы.
3.Так как
|
y = ±b |
x2 |
−a2 , |
|
a |
|
|
то |
|х|≥а. Поэтому гипербола |
расположена вне полосы, |
|
ограниченной прямыми x=±а.
4. Если x возрастает от а до +∞, то из (1.12) следует, что у возрастает от 0 до +∞ в первой координатной четверти.
5.
y = ±ba x
- наклонные асимптоты гиперболы.
По полученным свойствам строим гиперболу. Отрезок А1А2 и его длина 2а
называются действительной осью гиперболы, а
отрезок ОА1 и его длина а — действительной полуосью. Отрезок В1В2 и его длина 2b — мнимая ось гиперболы, а отрезок ОВ1 и его длина b—
мнимая полуось. Длина отрезка F1F2=2с
37

называется фокусным расстоянием, начало координат — центр гиперболы.
x2—у2=а2
Определение. Эксцентриситетом гиперболы называется величина
ε = ac .
Так как для гиперболы с > а, и следовательно, чем меньше ε, тем более сжата гипербола к оси ОХ.
Директрисы эллипса и гиперболы.
Определение. Прямые х=±(а/ε), где ε — эксцентриситет эллипса (гиперболы) называются директрисами эллипса (гиперболы).
Теорема. Отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса (гиперболы).
Доказательство, например для эллипса, следует из того, что
MF1=а+εх, МF2=а—εх.
Заметим, что, так как все точки параболы равноудалены от директрисы и фокуса, то отношение этих расстояний равно 1. Поэтому можно говорить об эксцентриситете параболы и считать его равным 1. Как уже отмечалось, эксцентриситет окружности равен нулю.
38

Фокальный параметр эллипса и гиперболы
Пусть эллипс и гипербола заданы соответственно своими каноническими уравнениями. Проведем через один из фокусов этих кривых прямую перпендикулярную оси ОХ и обозначим точки ее пересечения с кривой через Р и Р'.
Обозначим длину отрезка РР' через 2р. Тогда величина р(р>0) называется фокальным параметром эллипса (гиперболы) и
равна: p = ba .
Если обозначить через d – расстояние между фокусом и директрисой, то d = εp .
Так как для параболы ε = 1 и d = р, то делаем следующий Вывод: для эллипса (кроме окружности), гиперболы,
парабол фокальный параметр р равен: p = εd,
где c – эксцентриситет, d – расстояние от фокуса до соответствующей директрисы.
Заметим, что для окружности фокальный параметр равен ее радиусу.
Полярное уравнение эллипса, гиперболы, параболы
Выведем полярное уравнение для отличного от окружности эллипса, параболы или правой ветви гиперболы. Для этого совместим полюс полярной системы координат с левым фокусом эллипса (правым фокусом гиперболы) или единственным фокусом параболы, а
39

полярную ось направим перпендикулярно директрисе d, соответствующей фокусу. Обозначим через F, р и ε соответственно фокус, фокальный параметр и эксцентриситет кривой. Пусть М — произвольная точка кривой, МF = r— полярный радиус точки М, φ — ее полярный угол. Тогда
r = |
|
p |
1−ε cosϕ |
||
─ полярное уравнение эллипса, отличного от окружности, параболы, правой ветви гиперболы.
Для левой ветви гиперболы
r = |
|
|
− p |
|
1 |
+ε cosϕ |
|||
|
||||
─ полярное уравнение левой ветви гиперболы.
Классификация кривых второго порядка (КВП)
Уравнение вида
ax2+bху+су2+dx+еу+f=0, (1)
где a²+ b²+ c² ≠ 0 , называется уравнением кривой второго порядка в прямоугольноу системе ккординат OXY. Преобразуем систему координат таким образом, чтобы уравнение (1) приняло наиболее простой вид.
40
