1 / Алгебра и геометрия / Методички / pdf / Геометрия / Geometry

Свойства смешанного произведения.

1) число |a br c | равно объему параллелепипеда, построенного на

некомпланарных векторах a ,b ,c , приведенных к общему началу. В этом состоит геометрический смысл смешанного произведения.

2) (необходимое и достаточное условие компланарности трех векторов). Три вектора компланарны тогда и только тогда, когда их

смешанное произведение равно нулю. 3) (arr×b )rcr=ar(b ×crr)

4)a b c =b c a =c a b .

Линейная зависимость векторов.

Пусть дана система векторов

и α1, α2,...αn - действительные числа. Тогда векторы вида

α1a1 +α2a2 +... +αnan

называются линeйнoй комбинaциeй вeктоpов cиcтeмы (1).

Определение. Система векторов (1) называется линейно зависимой, если существует такая линейная комбинация этих векторов, равная нулевому вектору, т.е.

и хотя бы одно из чисел αi ≠ 0 .

Определение. Система (1) называется линейно независимой, если равенство (2) возможно тогда и только тогда, когда все числа αi=0.

Определение. Если какой-либо вектор a можно представить в

виде линейной комбинации векторов системы (1), т.е.

ar=α1a1 +α2a2 +... +αnan ,

то говорят, что вектор a линейно выражается через векторы системы (1).

Теорема. Для того чтобы векторы системы (1) были линейно зависимы (n>1), необходимо и достаточно, чтобы по крайней мере один из них линейно выражался через остальные.

11

Следствие. Если векторы системы (1) линейно независимы, то ни один из них нельзя линейно выразить через остальные. В частности, ни один из них не может быть нулевым.

Теорема. Для того чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

Следствие. Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.

Теорема. Любой вектор a на плоскости можно разложить по любым двум неколлинеарным векторам e1 и e2 этой плоскости, т.е.

представить в виде:

a =α1e1 +α2e2

причем это разложение единственно.

Теорема. Для того чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

Следствие. Три вектора линейно независимо тогда и только тогда, когда они некомпланарны.

Теорема. Любой вектор a можно разложить по трем некомпланарны векторам e1 ,e2 и e3 , т.е. представить в виде:

a =α1e1 +α2e2 +α3e3

причем это разложение единственно.

Tеорема. Любые четыре вектора линейно зависимы.

Определение. Говорят, что два лежащих в плоскости α линейно независимых вектора a и b (любые три линейно независимых

вектора ar,b и cr) образуют на этой плоскости (в пространстве) базис, если любой вектор, лежащий в этой плоскости α (любой вектор

пространства), может быть представлен в виде линейной комбинации векторов ar и b (ar,b ,cr).

Итак:

1)любая пара лежащих в данной плоскости неколлинеарнах векторов образует базис на этой плоскости;

2)любая тройка некомпланарных векторов образует базис в пространстве.

12

Координаты на прямой.

Прямая l, на которой задана точка 0, называемая началом координат, задан единичный вектор e , называемый ортом,

называется координатной осью.

Пусть М - произвольная точка прямой. Тогда вектор OM кол-

линеарен вектору er и, значит, OM = xer. Вектор OM называется

радиус-вектором точки М, а число х называется координатой точки

М на координатной оси l (обозначается: М(х)) или координатой

радиус-вектора OM (обозначается: OM =(х)).

Так как er - единичный вектор, то каждой точке М на оси l поставлено в соответствие вполне определенное действительное число – ее координата.

Обратно, для каждого действительного числа х найдется единственная точка М оси l, координата которой равна х. Таким образом, положение любой точки координатной оси однозначно определяется заданием координаты этой точки.

Координаты на плоскости.

Пусть на плоскости α заданы две координатные оси ОХ и OY с неколлинеарными ортами e1 и e2 cоответственно. Тогда тройка

(О,e1 ,e2 ) называется афинным репером, или афинной системой

координат плоскости α.

Точка 0 называется началом кооpдинат, векторы e1 и e2 —

базисными векторами. Если М – произвольная точка на плоскости α, то

OM = OM1 +OM 2 = xer1 + yer2

Числа х и у называются афинными координатами точки М в системе (0,e1 ,e2 ), причем х называется абсциссой, а у – ординатой

(записывается: М(х,у)). Вектор OM называется радиус-вектором точки М, числа х, у - координатами вектора OM (записывается:OM =(х,у)).

Афинная система координат (0,e1 ,e2 ) обозначается также OXY. Ось ОХ называется осью абсцисс, ось OY - осью ординат.

13

Теорема. Пусть a =α1a1 +α2a2 +... +αnan , где αi R

Тогда

Следствие 1. Пусть даны точки А (х1,y1) и В (х2,у2). Тогда

AB = (x2 − x1, y2 − y1 )

Следствие 2. Два вектора a = (х1,у1) и b = (х2,у1) коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, то есть

Афинная система координат (0,e1 ,e2 ), в которой орты e1 и e2

взаимно ортогональны, называется декартовой, или прямоугольной системой координат. В этом случае орты e1 и e2 обозначаются

соответственно ir и rj .

Координаты в пространстве.

Определение. Пусть в пространстве заданы три координатные оси OX, OY и OZ с некомпланарными ортами e1 ,e2 ,e3 соответственно.

Тогда четверка (0, e1 ,e2 ,e3 ) называется афинным репером, или

афинной системой координат в пространстве.

Точка 0 - начало координат, векторы e1 ,e2 ,e3 - базисные

векторы.

Так как векторы e1 ,e2 ,e3 - линейно независимы, то для

любого вектора ar = OM имеет место разложение: ar = OM = xe1 +ye2 +ze3

Числа x, y, z называются координатами точки М (записывается: М (х,у,z)), OM называется радиус-вектором точки М с координатами

х, у, z (записывается: OM = (х,у,z)), причем х называется абсциссой, у -

ординатой, z - аппликатой.

Афинную систему часто обозначают через OXYZ. Оси OX, OY, OZ называют соответственно осями абсцисс, ординат и аппликат. Плоскости, определяемые координатными осями, т.е. OXY, OYZ,

14

OXZ, называют координатными плоскостями. Эти плоскости делят все пространство на восемь частей, называемых координатными октантами.

Если упорядоченная тройка векторов e1 , e2 , e3 является

правой, то афинную систему называют правой, в противном случае - левой. В дальнейшем под афинной системой будем понимать правую систему. Если базисные векторы e1 , e2 , e3 попарно взаимно

ортогональны, то афинная система координат называется декартовой (прямоугольной), а базисные векторы обозначается соответственно

i , j,k .

В частности, если даны точки А (х1,у1,z1), В (х2,у2,z2), то

AB = (x2 − x1, y2 − y1, z2 − z1 )

Векторы a = (х1,у1,z1) и b = (х2,у2,z2) коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.

Скалярное произведение векторов в координатной форме.

Пусть в прямоугольной системе координат заданы векторы: ar= (х1,у1,z1), b = (х2,у2,z2). Тогда

a ·b = x1x2+y1y2+z1z2.

В частности

| ar|= ar2 = x12 + y12 + z12

Если даны точки А(х1,у1,z1) и В(х2,у2,z2), то, как известно, AB =(x2- х1,y2-у1,z2-z1) и значит.

| AB |= (x2 − x1 )2 +( y2 − y1 )2 +(z2 − z1 )2

-формула расстояния между двумя точками.

15

ее определитель ∆ есть число, которое вычисляется следующим образом:

∆ = а11а22а33 + а12а23а31 + а13а21а32 – а13а22а31 – а11а23а32 – а12а21а33.

Чтобы запомнить, какие произведения в правой части равенства берутся со знаком "+", а какие со знаком "–", полезно использовать следующее правило треугольников:

Легко проверить, что

- разложение определителя по элементам первой строки.

Векторное произведение векторов в координатной форме.

Пусть в прямоугольной системе координат заданы векторы ar = (x1,y1,z1), b = (x2,у2,z2). Тогда

Последнее равенство можно записать так:

Итак,

17

Тогда

Смешанное произведение векторов в координатной форме.

Пусть в прямоугольнойr системе координат заданы векторы a = (х1,у1,z1), b = (x2,y2,z2) и c = (x3,y3,z3). Тогда

x1 y1 z1 arbcr = x2 y2 z2

x3 y3 z3

Отсюда следует, что векторы a ,b и c компланарны тогда и только тогда, когда выполняется равенство:

x1 y1 z1

x2 y2 z2 =0 x3 y3 z3

Полярные координаты.

Возьмем на плоскости произвольную точку 0, которую назовем полюсом, и ось ОР, задаваемую единичным вектором e , которую назовем полярной осью. Тогда положение произвольной точки М плоскости можно определить двумя числами: r -

длина отрезка ОМ и φ - угол, который образует отрезок ОМ с осью ОР в положительном направлении, т.е. при движении против часовой стрелки.

18

Величины r и φ называются полярными координатами точки М, r-полярный радиус, φ-полярный угол. При этом считаем, что полярные координаты точек плоскости изменяются в следующих пределах: 0 ≤ r < ∞,0 ≤ϕ < 2π . Таким образом, получаем систему координат,

которая называется полярной системой координат.

С прямоугольными координатами полярные связаны следующими соотношениями:

х = r cosφ, у = r sinφ.

Так как х2 + у2 = r2, то

Прямоугольные координаты на плоскости.

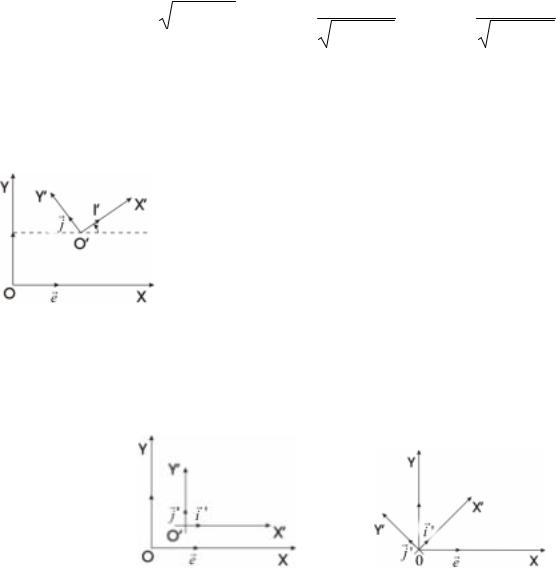
Пусть дана старая и новая прямоугольные системы координат, соответственно (0,i , j ) и (О',ir', rj '). Обозначив через φ угол между векторами

iи i '. Тогда

x= x'cosφ - y'sinφ + α,

y = x'sinφ + y'cosφ + β

В частности, если ir=ir' и j = j ', то формулы принимают вид

x = х' + α, у = у' + β

- формулу преобразования координат при параллельном переносе системы координат

Если же точки 0 и 0' совпадают, то

19

x = x'cosφ - y'sinφ,

y= x'sinφ + y'cosφ.

-формулы преобразования координат при повороте системы координат вокруг начала на угол φ

ПРЯМАЯ НА ПЛОСКОСТИ.

Прямая на плоскости

Пусть в плоскости α задана афинная система координат (0,e1 ,e2 ) и прямая l, принадлежащая этой

плоскости α. Составим уравнение прямой l. Заметим, что положение прямой l однозначно определено, если известен вектор, коллинеарный этой прямой и

называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять любой вектор, коллинеарный данной прямой. Пусть r1 = (m1,n1) и r2 =(m2,n2) - какие-либо направляющие векторы

прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов

- угловой коэффициент относительно выбранной системы координат. r r

В частности, для прямоугольной системы координат (0,i , j )

k = tgα, где α – угол между осью ОХ и любым направляющим вектором прямой l. Угол α называется углом наклона прямой l к оси ОХ.

20