
1 / Алгебра и геометрия / Методички / pdf / Геометрия / Geometry
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования «Гомельский государственный университет имени Франциска Скорины»
А.Д. Ходалевич Р.В. Бородич В.Н. Рыжик
«Аналитическая геометрия »
Тексты лекций
Гомель, 2004
УДК 514 (078) ББК 22.151 Я73 Х 69
Рецензенты: Семенчук В.Н. – профессор, доктор физикоматематических наук кафедра высшей математики учреждения образования «Гомельский государственный университет имени Франциска Скорины».
Рекомендован к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины» 24 марта 2004 года, протокол № 7
Ходалевич А.Д.
Х 69 Аналитическая геометрия: Тексты лекций. /А.Д.Ходалевич,
Р.В.Бородич, В.Н. Рыжик. − Гомель: УО «ГГУ им. Ф.Скорины»; 2004 − 65с.
Дается краткое изложение курса лекций по аналитической геометрии для студентов, обучающихся по специальности «Прикладная математика»
УДК 514 (078) ББК 22.151 Я73 Х 69
©А.Д. Ходалевич, Р.В. Бородич, В.Н. Рыжик, 2004
©Учреждение образования «Гомельский государственный университет имени Франциска Скорины», 2004
2
СОДЕРЖАНИЕ
1.Векторы и координаты………………………………….…4
2.Прямая на плоскости………………………………………20
3.Плоскость…………………………………………………...25
4.Прямая в пространстве. Взаимное расположение
прямой и плоскости в пространстве…………………………29
5.Кривые второго порядка…………………………………...33
6.Поверхности второго порядка……………………………..56
Литература………………………………………………….….64
3

Аналитическая геометрия - это раздел математики, в котором геометрические объекты изучаются с помощью алгебраических методов, в основе которых лежит понятие координат.
ВЕКТОРЫ И КООРДИНАТЫ
Понятие вектора
Пусть А – произвольное непустое множество. Декартовым
кваратом А называется множество
A2 ={(a,b) | a,b A}
Бинарным отношением на А называется любое подмножество ϕ
множества A2.
Отношением эквивалентности на А называется такое бинарное отношение ϕ на А, которое удовлетворяет следующим условиям:
1) (a,a) ϕ, a A |
(рефлексивность); |
2)если (a ,b) ϕ, то (b,a ) ϕ (симметричность);
3)если (a ,b) ϕ,(b,c) ϕ, то (a ,c) ϕ (транзитивность).
Теорема. Любое отношение эквивалентности на множестве А определяет разбиение этого множества на попарно непересекающиеся классы (классы эквивалентности). Обратно, любое разбиение множества А на попарно непересекающиеся классы определяет отношение эквивалентности на А.
Направленный отрезок – отрезок, у которого указано, какая точка является началом, а какая концом. Обозначается AB .
Пусть заданы направленные отрезки AB и CD , не лежащие на двух различных параллельных прямых, и плоскость α , проходящая через точки В и D. Тогда плоскостьα разбивает все пространство на два полупространства. Если при этом точки B и D лежат в одном
полупространстве, то говорят, что направленные отрезки |
|
AB |
и |
CD |
|
||||||||
одинаково |
направлены (обозначается |
|
↑↑ |
|
). |
В |
противном |
||||||
AB |
CD |
||||||||||||
случае, |
они |
называются |
противоположно |
направленными |
|||||||||
(обозначается AB ↑↓ CD ).
Если направленные отрезки AB и CD лежат на одной прямой, то они одинаково (противоположно) направлены, если существует такой
третий направленный отрезок EF , который одинаково направлен с
4

каждым из направленных отрезков AB и CD (противоположно направлен в точности с одним из направленных отрезков AB или
CD ).
Абсолютной величиной или модулем (длиной) направленного отрезка ar называется длина этого направленного отрезка и обозначается |ar|.
Два направленных отрезка a и b называются равными, если a = b и a ↑↑ b , при этом пишут a =b ,
Теорема. Отношение равенства направленных отрезков является отношением эквивалентности.
Тогда вектором называется абстрактный объект, совпадающий с некоторым классом эквивалентности.
Таким образом, каждый из равных друг другу направленных отрезков считается представлением (изображением) данного вектора, а неравные направленные отрезки считаются представлением разных векторов. Поэтому в дальнейшем вектор изображается точно так, как и соответствующий ему направленный отрезок.
Векторы a и b называются коллинеарными, если образующие их направленные отрезки параллельны одной и той же прямой
(обозначается a ||b ).
Три и более векторов называются компланарными, если образующие их направленные отрезки параллельны некоторой плоскости.
Нулевым вектором называется вектор, начало которого совпадает
с его концом (обозначается 0). Направление нулевого вектора не определено.
Линейные операции над векторами.
Определение. Суммой a +b векторов a и b называется вектор,
проведенный из начала a к концу b , если конец a и начало b совпадают. Приведенное определение сложения векторов называется
правилом треугольника. Векторы a и b можно складывать, пользуясь
правилом параллелограмма.
5
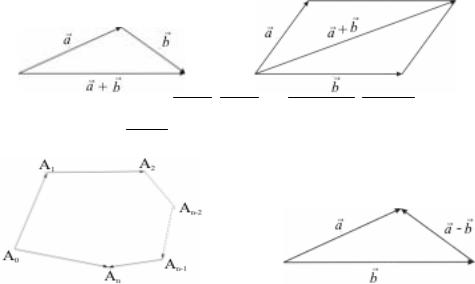
Если имеется n векторов A0 A1, A1 A2 ,..., An−2 An−1, An−1 An , то их сумма определяется как вектор A0 An .
Определение. Разностью векторов a и b называется такой
вектор c =a -b , что выполняется равенство c +b =a .
Легко показать, что для любого вектора a , существует такой
единственный вектор b , называемый противоположным вектору a |
|||||
что |
ar+b =0. |
Вектор, |
противоположный вектору ar, |
будем |
|
обозначать –a . |
|
|
|
|
|
Определение. Произведением вектора a на число λ |
(λ≠0) |
||||
называется вектор b =λar |
, удовлетворяющий следующим условиям: |
||||
1) |
векторы ar |
и |
b |
одинаково направлены, если |
λ>0, и |
противоположно направлены, если λ<0; |
|
||||
2) |
|br|=|λ|| a |. |
|
|
|
|
По определению, произведение произвольного вектора a на число
0 есть нулевой вектор, т.е. 0a =0.
Введенные операции сложения векторов и умножение вектора на число называются линейными. Они обладают следующими свойствами:
1) сложение векторов коммутативно:
|
a +b =b +a , a ,b ; |
2) |
сложение векторовrассоциативно: |
|
(a +b )+c = a +(b +c ), a ,b ,c ; |
3) ar+0= ar, a ; |
|
4) |
a +(-a )=0, a ; |
5) |
умножение вектора на число ассоциативно: |
|
α (β ar) = (α β)a , a α, β R; |
6) |
1a =a , a ; |
|
6 |

7) умножение вектора на число дистрибутивно по отношению к сложению чисел:
(α+β)a =αa +βa , a , α, β R;
8) умножение вектора на число дистрибутивно по отношению к сложению векторов:
α(a +b )=αa +αb , a ,b , α R;
Множество всех векторов пространства (плоскости), удовлетворяющих свойствам 1) – 8), называется линейным, или
векторным пространством, и обозначается R3 ( R2 ).
Теорема (необходимое и достатаочное условие коллинеарности
двух векторов). Для того чтобы векторы a и b были коллинеарны, необходимо и достаточно, чтобы существовало число λ, удовлетворяющее условию:
b = λa .
Проекции.
Назовем осью прямую, на которой указано направление, которое будем называть положительным.
Пусть l - некоторая ось, α - плоскость, непараллельная оси l. Через произвольную точку А пространства проведем плоскость α'||α и обозначим точку пересечения плоскости α' c осью l через А1. Тогда точка А1 называется проекцией точки А на ось l относительно плоскости α. В частности, если α l, то проекция называется
прямоугольной, или ортогональной.
Пусть теперь задан вектор AB . Возьмем проекции А1 и В1 точек А и В на ось l относительно плоскости α.
Тогда вектор A1B1 называется проекцией вектора AB на ось l
относительно плоскости α. Величиной проекции вектора AB на ось l
относительно плоскости α называется число, равное:
7

а) | A1B1 |, если направление вектора A1B1 совпадает с направлением оси l;
б) - | A1B1 |, если направление A1B1 противоположно направлено
оси l.
Обычно из контекста ясно о проекции относительно какой плоскости идет речь. Поэтому величину проекции вектора AB на ось l
будем обозначать Прl AB , а для ортогональной проекции использовать
обозначение прl AB .
Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l1 || l и обозначим точку пересечения прямой l1 с плоскостью α через А1. Точка А1 называется
проекцией точки А на плоскость α относительно прямой l.
Если прямая l α, то проекция называется прямоугольной, или
ортогональной.
Определение. Углом между двумя векторами, или между осями, или между вектором и осью называется наименьший угол α, на который надо повернуть один из векторов или одну из осей до совпадения по направлению с другим вектором или осью.
Из определения следует, что 0≤α≤π. Угол между векторами или между осями, или между вектором и осью будем обозначать
соответственно: (ar ^b ), (l ^l |
2 |
), (a ^l ). |
|
' |
1 ' |
' |
|
Теорема. Проекция вектора на ось обладает следуицики свойствами:
1)прl a =| a | cos(a ^' l);
2)Прl λa = λПрl a, λ R;
3)Прl (ar +b) = Прl ar + Прlb .
Скалярное произведение векторов.
Определение. Скалярным произведением векторов
a иb называется число (которое обозначается a b ), равное произведению длин этих векторов на косинус угла между ними, т.е.
8

r |
r |
r |
ab =| a || b | cos(a ^b) . |
||
|
|
' |
Из первого пункта предыдущей теоремы сразу следует, что |
||
|
|
arb =| b | прbrar =| ar| прarb . |
Так как соs 0 = 1. то a a =|a |2. Следовательно, |
||
где выражение ar |
ar |
| ar|= ar2 , |
=ar2 называется скалярным квадратом вектора |
||
a .
Теорема. Скалярное произведение двух векторов обладает
rrсвойствами:
1)a b =b a (коммутативность);
2)λ (ra b ) = (λa )b , λ R;
3)a (b +c ) =a b + a c (дистрибутивность).следующими
Из определения следует, что
r |
r |
arb |
|
|
cos(a |
^b) = |
r |
r |
. |
|
' |
| a || b | |
||
|
|
|
|
|
Tеорема (необходимое и достаточное условие ортогональности двух векторов). Два ненулевых вектора взаимно перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю.
Векторное произведение двух векторов.
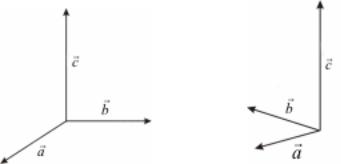
Определение. Упорядоченная тройка некомпланарных векторов a ,b ,c называется правой, если при приведении их к общему началу
поворот от вектора a к вектору b по кратчайшему пути виден с конца вектора c против часовой стрелки. Если же такой поворот
осуществляется по часовой строже, то вектора a ,b ,cr образуют левую тройку векторов.
1) |
2) |
9
Определение. Векторным произведением двух векторов a и b
называется вектор cr, обозначаемый a ×b и удовлетворяющий
r:
1)|c |=|a | |b | sin (a ^,b );
2)cr ar, c b ;r
3)векторы a ,b ,c образуют правую тройку векторов.
Свойства векторного произведения.
1)(Необходимое и достаточное условие коллинеарности двух r и b коллинеарны тогда и только тогда, когдавекторовследующим
ar×b =0.
2) (геометрический смысл векторного произведения) число |a ×b |
равно площади параллелограмма, построенного на неколлинеарных |
||
векторах ra и brr |
, приведенных к общему началу. |
|
3)a ×b = –b |
×a , (антикоммутативность). |
|
4) (λa ) ×br=λ ( a ×br), λ R |
||
5) ar× (rλb )=λ ( ar×b )r. |
||
6) (a +b )×c = a ×c +b |
×c (дистрибутивность). |
|
7) cr× (ar-b )=c ×ar+cr |
×b (дистрибутивность). |
|
Смешанное произведение векторов.
Определение. Смешанным произведением векторов a ,b ,c
называется число, равное (a ×b )c и обозначается a b c .
10
