Практическое руководство для студ. экон. спец. 3 ч

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гомельский государственный университет им. Франциска Скорины

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Итак, область сходимости ряда

Итак, область сходимости ряда

.pdf

Скачиваний:

Добавлен:

09.03.2016

Размер:

573.73 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

ограничена сверху графиком функции y y2 (x), снизу графиком функции y y1(x)(рисунок 5.4).

Пусть АА1В1В ─ минимальный прямоугольник, в котором заключена данная область S. Тогда для непрерывной в области S функцииy f (x;y)

																																			b				d
																					f (x; y)dxdy = dx f (x; y)dy .
																						S													a				c
			Если же область S является стандартной в направлении																																																		оси			Ox и
определяется неравенствами c y d , x1(y) x x2 (y) , то
																																f (x; y)dxdy									d		x2 (y)
																																f (x; y)dxdy								=	dy			f (x; y)dx.
																																S									c x1(y)
																				Пример5.1.Вычислить xydxdy,если
																																									S
																				S= (x; y):1 x 2,1 y 3 (Рисунок5.5).
																				Решение.																		Область										S							является
																		прямоугольником,																																					поэтому
																																	2				3				2				2	1		3		2		9			1
																																	2				3				2				2	1		3		2		9			1
																										xydxdy= dx xydy= (xy																					)		dx= (					x			x)dx=
																										xydxdy= dx xydy= (xy																					)		dx= (					x			x)dx=
																											S						1				1				1					2		1		1		2			2
																											S						1				1				1					2				1		2			2
	9	2				1	2				9				1		2									2		2										1
	9					1					9				1										x													1
=			xdx					xdx			=					xdx=															=		4 2						= 6.
=	2		xdx			2		xdx			=					xdx=						4						1			=		4 2						= 6.
	2	1				2	1				2				2		1							2				1										2
			Пример 5.2. Вычислить (x2 xy 2y2 )dxdy																																					по области
																						S
			S = (x; y):0								x 1,0 y 1 x (Рисунок 5.6).
			Решение. Область интегрирования изображена на рисунке. Имеем
																															1		1 x
											(x2				xy 2y2 )dxdy = dx (x2																						xy 2y2 )dy=
											S																				0		0
													1		2				y2				2 3						1 x					1			2					(1 x)					2	2						3
													1		2				y2				2 3						1 x					1			2					(1 x)					2	2						3
											=																						dx=																								=
																					y																													(1 x)
														x y x							y										0					x (1 x) x									2					(1 x)					dx
											0								2 3												0		0												2			3
											0																						0
											1			x2 x3						1														2	(1 3x 3x2 x3 ) dx=
											=									1	(x 2x2 x3 )													2
											=										(x 2x2 x3 )
											0								2														3
													1		7 3						2	3								2							7 x4			2 3			3 2					2			1
													1		7 3						2	3								2							7 x4			2 3			3 2					2			1
											=																																									=
																	x 2x									x															x x						x
															6		x 2x									x						dx=									x x						x
											0				6							2								3							6 4 3						4					3			0
											0																			3																					0
=			7		2			3		2		7 16 18 16														7		.
=																												.
		25		3			4		3							24										24

Замечание 5.1. Если область интегрирования S не удовлетворяет условиям стандартной области, каждая из которых была бы стандартной в направлении одной из осей, и вычислить двойные интегралы по каждой части отдельно.

5.2 Тройной интеграл и его свойства

По аналогии с двойным интегралом вводится понятие тройного интеграла.

Рассмотрим ограниченную замкнутую пространственную область V и определённую в ней непрерывную функцию u f (x;y;z). Аналогично строится интегральная сумма по данному объёму и определяется тройной интеграл от функции f (x;y;z) по пространственной области V:

	n
f (x; y;z)dV = im f (xk ; yk ;zk ) Vk
V	0 k 1
или	n
	n
f (x; y;z)dxdydz= im f (xk ; yk ;zk ) Vk .
V	0 k 1

Тройной интеграл обладает свойствами, аналогичными свойствами двойного интеграла.

Предположим, что область V является стандартной в направлении оси Oz, т. е. удовлетворяет следующим условиям:

1)всякая прямая, параллельная оси Oz и имеющая с данной областью общие точки, пересекает границу области только в двух точках;

2)проекция S области V на плоскость Oxy представляет собой

стандартную область в направлении оси Ox или оси Oy .
Если	стандартная область	V		ограничена		сверху	поверхностью
z z2 (x; y),	снизу – поверхностью		z z1(x; y), а			проекция	S области V
стандартна в направлении оси Oy			и определяется неравенствами a x b,
y1(x) y y2 (x), то				y2 (y) z2 (x;y)
			b	y2 (y) z2 (x;y)
	f (x; y;z)dxdydz= dx dy				f (x;y;z)dz.
	V		a	y1(y) z1(x;y)
Замечание 5.2. Если область S является стандартной в направлении
оси Ox и определяется неравенствами				x1(y) x x2 (y) , c y d , то
			b	x2 (y) z2 (x;y)
	f (x; y;z)dxdydz= dx dy				f (x;y;z)dz.
	V		a	x1(y)	z1(x;y)

Замечание 5.3. Если область V является стандартной в направлении каждой координатной оси и её проекции на координатные плоскости являются стандартными в направлении каждой соответствующей оси, то пределы интегрирования в трёхкратном интеграле можно расставить шестью различными способами.

Замечание 5.4. Если V ─ прямоугольный параллелепипед, определяемый неравенствами a x A , b y B, c z C , то

d B C

f (x; y;z)dxdydz=	dx dy f (x; y;z)dz.
V	c b c

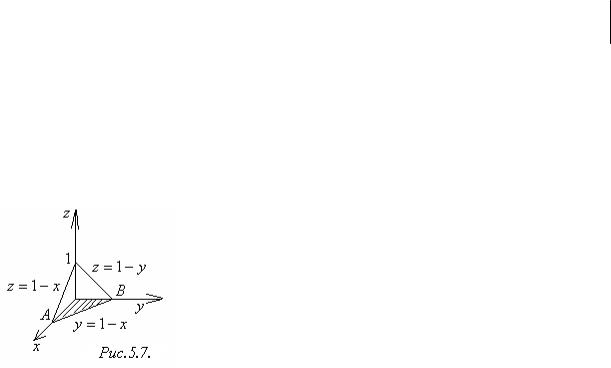
Пример 5.3. Вычислить				(x y z)dxdydz ,			где	V –	параллелепипед,
				V
ограниченный плоскостями x 1,x 1, y 0, y 1,z 0,z 2.
Решение. По замечанию 5.3 имеем
	1	1	2	1		1	z2	2

								dy =

(x y z)dxdydz = dx dy (x y z)dz = dx xz yz							2
V	1	0	0		1	0		0
										1 =
1	1		1			1		1

= dx 2x 2y 2 dy= (2xy y2 2y)					1dx= (2x 1 2)dx= (2x 1)dx= x2 x
1	0		1		0	1		1		1

= 1 1 1 1 2.

Пример 5.4. Вычислить интеграл (x y z)dxdydz, где V ─ пирамида,

ограниченная плоскостью							V		и		координатными				плоскостями
ограниченная плоскостью			x y z 1						и		координатными				плоскостями
x 0, y 0,z 0 (Рисунок 5.7.).
		Решение. Область V проектируется на плоскости
Oxy в треугольник АОВ, ограниченный прямыми
x 0, y 0, y 1 x. Имеем
						1					1 x	1 x y
(x y z)dxdydz= dx dy												(x y z)dz=
V						0					0	0
	1	1 x			z2			1 x y
	1	1 x			z2			1 x y
= dx												dy=

			xz yz		2				0
	0	0			2				0
	0	0								1 x
=	1	1		2	2		y3			1 x		1 1		3	1

											dx		(2 3x x )dx
	2	y yx xy				3					dx		(2 3x x )dx
	2	0				3					0	6	0		8
		0											0

Вопросы для самоконтроля

1.Что называется двойным интегралом от функции двух независимых переменных по данной области? Укажите геометрическое толкование двойного интеграла.

2.Перечислите основные свойства двойного интеграла.

3.Что называется повторным интегралом?

4.Укажите способ вычисления двойного интеграла в случае, когда область интегрирования есть прямоугольник, стороны которого параллельны координатным осям.

5.Как вычислить двойной интеграл с помощью двукратного в случае произвольной области интегрирования в прямоугольной системе координат?

6.Что называется тройным интегралом от функции трех независимых переменных по данной области?

7.Какая область называется стандартной в направлении оси Oz?

8.Как вычисляется тройной интеграл в декартовой системе координат?

9. Как вычисляется тройной интеграл, если область является прямоугольным параллелепипедом?

6 Числовые и функциональные ряды

6.1 Основные понятия и свойства числовых рядов

Пусть дана бесконечная последовательность чисел a1,a2 ,...,an ,.... Символ

a1 a2 ... an ...

обозначаемый an , называется числовым рядом или просто рядом, а

n 1

числа a1,a2 ,...,an ,... членами числового ряда. Суммы конечного числа

членов ряда S1 a1, S2 a1 a2 , S3 a1 a2 a3, …,Sn a1 a2 ,,, an ,...

называются частными суммами (или отрезками) числового ряда.

Рассмотрим последовательность		S1,S2 ,S3,...,Sn ,.... Если существует предел
S im Sn , то числовой ряд		называется сходящимся, а число S
	an
n	n 1
суммой этого ряда. В этом случае пишут

S	= a1 a2 ... an ...= an .

n 1

Если же последовательность S1,S2 ,S3,...,Sn ,... не имеет предела, то ряд называется расходящимся. Такой ряд суммы не имеет.

Пример 6.1. Рассмотрим ряд, составленный из членов геометрической

прогрессии 1,q,q2 ,...,qn 1,...: 1 q q2 ... qn 1

....

Если q 1, то Sn =1 q q2

... qn 1=

qn 1q 1

1 qn

q 1

1 q

Если

прогрессия

бесконечно

убывающая,

т.

е.

то im Sn =

1 qn

n 1 q

1 q

Это означает, что при

1 ряд расходится и его сумма равна

1 q

При q 1

получаем ряд 1+1+1+…+1+…. Тогда Sn

= n и im Sn = , т. е.

при q 1 ряд расходится.

Пример 6.2. Исследовать на сходимость ряд n 1

n(n 1)

Очевидно, что

n 1,2,... .

n(n 1)

n 1

Поэтому Sn =

...

, откуда

n 1

im Sn

= im 1

n 1

Следовательно, данный ряд сходится и его сумма равна 1. Свойства числовых рядов.

Свойство 6.1. Если в ряде an = a1 a2 ... an ... отбросить конечное

n 1

число m первых членов, то получим ряд

am 1 am 2 ... am n ...,

который называется m-ым остатком данного ряда. m-ый остаток данного ряда сходится (или расходится) одновременно с данным рядом. Это означает, что при исследовании ряда на сходимость можно игнорировать конечное число его первых членов.

Свойство 6.2. Необходимый признак сходимости ряда:

общий член an сходящегося ряда

стремится к нулю при n , т. е.

n 1

im an = 0.

Это означает, что если im an 0, то ряд an расходится.

n 1

Пример 6.3. Рассмотрим снова ряд qn 1 из примера 1 при

1. Тогда

n 1

qn 1

n 1

1 и, следовательно,

im an =

im qn 1 0, т.е. ряд

при

расходится.

Пример 6.4. Рассмотрим ряд 1

...

...,

который называется гармоническим рядом. Отметим, что

im an

= im

= 0 .

n n

Однако это ничего не говорит о сходимости данного ряда. Если предположить, что гармонический ряд сходится и его сумма равна S , то

im Sn = S

и im S

. Тогда im

= im

S2n im Sn =S S 0.

Однако это противоречит тому, что

2n Sn

...

n 1

n 2

2n 2

Следовательно, гармонический ряд расходится.

Свойство 6.3. Если ряд an сходится и его сумма равна S , то ряд

n 1

can , где c произвольное число, также сходится и его сумма равна cS .

n 1

Свойство 6.4. Если ряды an и bn сходятся и их суммы

n 1 n 1

соответственно равны S1 и S2 , то ряд an bn также сходится и его сумма

n 1

S S1 S2 .

6.2 Сходимость числовых рядов 6.2.1 Сходимость рядов с положительными членами

Положительным рядом называется ряд, члены которого неотрицательны.

Признак сравнения рядов. Пусть даны два положительных ряда

	=a1 a2		(6.1)
an	=a1 a2	...	(6.1)
n 1
	=b1 b2		(6.2)
bn	=b1 b2	...	(6.2)

n 1

Если выполняется условие an bn n 1,2,... , то из сходимости ряда (6.2) следует сходимость ряда (6.1), а из расходимости ряда (6.1) следует расходимость ряда (6.2).

Пример 6.5. Исследовать на сходимость ряд

n 1 n 1

В примере

6.2

мы

доказали, что

ряд

n 1

сходится.

Так

как

n n 1

n 1,2,... , то по признаку сравнения ряд

также

n 1

n n 1

n 1

сходится.

таковы,

Признак Даламбера. Если члены положительного ряда an

n 1

что существует предел im

an 1

, то при 1 ряд расходится,

а при 1

сходится.

Пример 6.6. Рассмотрим ряд

. Для этого ряда

an 1

n 1

n 1!

Тогда im

an 1

= im

n an

n 1! n!

n 1!

n n 1

По признаку Даламбера ряд

сходится.

n 1

Интегральный признак Коши. Пусть члены положительного ряда

	такие, что a1 f (1),a2		f (n),..., где функция	f (x)при x 1
an	такие, что a1 f (1),a2	f (2),...,an	f (n),..., где функция	f (x)при x 1
n 1

непрерывна, положительна убывает. Тогда данный ряд и несобственный


интеграл f (x)dx	сходится или расходится одновременно.
1
				1	0 .
Пример 6.7. Рассмотрим ряд n 1
Пример 6.7. Рассмотрим ряд n 1				n
Функция f (x)	1	,	x 1, удовлетворяет условиям, указанным в
Функция f (x)		,	x 1, удовлетворяет условиям, указанным в
	x

интегральном признаке. Исследуем интеграл

	dx		x	1	b		b	1			1			,					если 1
				1				1						,
		im				im										1						.

1 x																		,	если 1
		b 1			1	b 1
		b 1			1	b 1
														1
									1
Следовательно, ряд												сходится при 1										и расходится при 0 1.
Следовательно, ряд									n			сходится при 1										и расходится при 0 1.
						n 1			n
	6.2.2 Сходимость знакочередующихся рядов
	Определение 6.1. Знакочередующимся рядом называется ряд вида
где an						a1 a2						a3		a4 ... ( 1)n 1an								...,		(6.3)
где an		0,n 1,2,...
	Признак Лейбница. Если члены знакочередующегося ряда (6.3)
удовлетворяют условиям: а) an 1																an (n 1,2,...;						б)		im an =0,
то знакочередующийся ряд сходится.																								n
то знакочередующийся ряд сходится.
	Пример 6.8. Знакочередующийся ряд
										1			1		1		1			1	... 1 n 1		1		...
										1											... 1 n 1				...
											2			3		4			5				n

так как условия теоремы Лейбница здесь выполнены.

6.2.3 Абсолютная и условная сходимость рядов

Перейдём теперь к рядам с членами, имеющими любой знак. С каждым

таким рядом		(6.4)
	an

n 1

связан ряд с неотрицательными членами, составленный из модулей членов данного ряда, т. е. ряд

	(6.5)
an

n 1

Определение 6.2. Ряд (6.4) называется абсолютно сходящимся, если ряд (6.5) сходится. Если же ряд (6.4) сходится, а ряд (6.5) расходится, то ряд (6.4) называется условно сходящимся.

Теорема 6.1. Если ряд сходится абсолютно, то он сходится.

1 n 1

Пример 6.10. Ряд n 1

абсолютно сходится при 1 (см. пример

6.11). Этот

ряд сходится

условно

при

0 1. Действительно, ряд

1 n 1

сходится при 1 и расходится при 0 1, как доказано

n 1

1 n 1

в примере 6.7. Однако при

0 1

ряд n 1

сходится по признаку

Лейбница.

6.3 Функциональные ряды

Будем рассматривать ряды, членами которых являются не числа, а

функции:	u1(x) u2 (x) ... un (x) ...		(6.6)
Такие ряды называются функциональными.
Например, ряд
	1 x x2 ... xn ...
является функциональным.
Если в ряде (6.6)	положим x x0 , где x0	значение из	области
определения функций un (x), n 1,2,..., то получим числовой ряд			(6.7)
	u1(x0 ) u2 (x0 ) ... un (x0 ) ...		(6.7)

Если ряд (6.7) сходится, то x0 называется точкой сходимости ряда (6.6). Если же ряд (6.7) расходится, то точка x0 называется точкой расходимости ряда (6.6).

Определение 6.3. Совокупность всех точек сходимости функционального ряда называется областью его сходимости.

6.4 Степенные ряды Определение 6.4. Степенным рядом называется функциональный ряд

вида

a0 a1x a2 x2 ... an xn ..., (6.8)

где a0 ,a1,a2,...,an ,... действительные числа, называемые коэффициентами степенного ряда.

1) Если степенной ряд сходится лишь в точке x 0, то он относится к рядам первого класса.

Например, ряд

1 x 2!x2 3!x3

... n!xn ...

(6.9)

относится к рядам первого класса.

Зафиксируем x 0

и рассмотрим

числовой ряд

3 ... n!

n ...

По признаку Даламбера

n 1

im n 1 =

n n!

и ряд расходится при всех x 0. Следовательно, ряд (6.9) сходится только при x 0.

2) Если ряд (6.8) сходится на всей числовой прямой, то он относится к рядам второго класса.

Например, применив признак Даламбера при фиксированном x, нетрудно убедиться, что к рядам второго класса относится ряд

1 x x2 ... xn ...

1! 2! n!

3) Ряд (6.8), не принадлежит первому и второму классам, его относят к рядам третьего класса.

Теорема 6.2. (теорема Абеля). Если степенной ряд (6.8) сходится при

x x0 0,	то он абсолютно сходится для любого x, удовлетворяющего
условию	x	x0	; если же степенной ряд (6.8) расходится при x x0 , то он

расходится и при любом x, удовлетворяющем условию x x0 . Следствие. Для каждого степенного ряда (6.8) третьего класса

существует число R 0, называемое радиусом сходимости этого ряда, для которого выполняется условие: при x R ряд (6.8) сходится абсолютно, при x R ряд (6.8) расходится.

Промежуток R;R называется интервалом сходимости степенного ряда. Для степенного ряда (6.8) второго класса интервал сходимости

; .

Областью сходимости степенного ряда (6.8) является интервал R;R , к которому в отдельных случаях добавляется один или оба конца этого интервала (это исследуется для конкретных рядом при x R и x R ).

Для степенного ряда (6.8) первого класса полагают R 0; для степенного ряда (6.8) второго класса R .

Теорема 6.3. Пусть для степенного ряда (6.8) существует и отличен от

нуля предел
	an 1	L. Тогда R	1	.
im			1
im
n	an		L

Пример 6.11. Найти область сходимости степенного ряда 1 n 5n xn .

n 0

1 5x 52 x2 ... 1 n 5n xn ....

Решение. 1 n 5n xn =

n 0

1 n 1

Рассмотрим im

an 1

5n 1

= 5. Тогда R

. Итак,

1 1

;

1 n

интервал сходимости.

Исследуем ряд на концах интервала.

1 n

. Имеем ряд 1

= 1.

n 0

Этот ряд расходится согласно необходимого признака сходимости рядов.

	1				5n	1	n
2) x		. Имеем ряд 1 n					= 1 n .
	5
				n 0	5		n 0
Тогда	Sn		0,	если n нечётное
			1,	если n чётное

Поэтому im Sn не существует и ряд 1 n расходится.

n 0

Вопросы для самоконтроля

1.Что называется числовым рядом, общим членом ряда?

2.Что называется частичной суммой ряда?

3.Что называется суммой ряда?

4.Какой ряд называется сходящимся, расходящимся?

5.В чем состоит необходимый признак сходимости ряда?

6.Какой ряд называется гармоническим? Выполняется ли для него необходимый признак сходимости? Сходится ли гармонический ряд?

7.Сформулируйте достаточные признаки сходимости, основанные на сравнении рядов с положительными членами.

8.Сформулируйте признак Даламбера сходимости рядов с неотрицательными членами.

9.Сформулируйте интегральный признак Коши сходимости рядов с неотрицательными членами.

10.Какой ряд называется знакочередующимся?

11.Сформулируйте признак Лейбница.

12.Какой ряд называется абсолютно сходящимся; условно сходящимся?

13.Дайте определение функционального ряда, его области сходимости.

14.Какой ряд называется степенным?

15.Что называется радиусом сходимости, интервалом сходимости, областью сходимости?

16.По какой формуле вычисляется радиус сходимости?

7 Дифференциальные уравнения первого порядка

7.1 Основные понятия Дифференциальным уравнением называется соотношение,

связывающее независимую переменную x, искомую функцию y f (x) и её производные. Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком данного уравнения. Следовательно, общий вид ДУ n-го порядка следующий.

F x, y, y , y ,...,y		= 0.	(7.1)
	(n)
Например, уравнения
а) y yx x2 ,	б) y y 1

соответственно ДУ 1-го и 2-го порядков.

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.03.2015221.18 Кб166ПРАКТИЧЕСКИЕ ЗАНЯТИЯ по психологии семьи.doc
#
25.03.20155.92 Mб95Практический психолог в школе.pdf
#
25.03.20151.57 Mб9Практическое пособие по вирусологии.pdf
#
09.03.2016603.35 Кб3Практическое руководство для студ. экон. спец. 1 ч.pdf
#
09.03.2016621.5 Кб6Практическое руководство для студ. экон. спец. 2 ч.pdf
#
09.03.2016573.73 Кб9Практическое руководство для студ. экон. спец. 3 ч.pdf
#
09.03.2016264.7 Кб32Практическое руководство к семинарским занятиям ч.1.doc
#
09.03.201680.15 Кб19Практическое руководство к семинарским занятиям ч.2.docx
#
06.08.201969.12 Кб7превращения веществ.doc
#
15.07.2019197.77 Кб3Преддипломная работа.docx
#
16.12.2018101.89 Кб3Предлагаемое исследование поэзии Марины Цветаев....doc