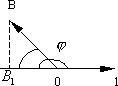-
Для любых чисел a и b и любого вектора
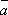 выполняется
равенство
выполняется
равенство  .
. -
Разность векторов.
Вектор,
коллинеарный данному вектору ![]() ,
равный ему по длине и противоположно
направленный, называется противоположнымвектором
для вектора
,
равный ему по длине и противоположно
направленный, называется противоположнымвектором
для вектора ![]() и
обозначается
и
обозначается ![]() .
Противоположный вектор
.
Противоположный вектор ![]() можно
рассматривать как результат умножения
вектора
можно
рассматривать как результат умножения
вектора ![]() на
число λ = –1:
на
число λ = –1: ![]() .
.
Разностью двух
векторов ![]() и
и ![]() называется
вектор
называется
вектор ![]() ,
равный сумме векторов
,
равный сумме векторов ![]() и
и ![]() ,
т.е.
,
т.е. ![]() .
.
Очевидно,
что ![]() ,
для любого вектора
,
для любого вектора ![]() .
.
Легко
показать, что ![]() .
.
Действительно, 
Таким
образом, если ![]() .
.
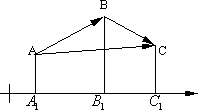
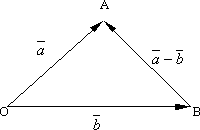
Из
определения суммы двух векторов вытекает
правило построения вектора разности.
Откладываем векторы ![]() и
и ![]() из
общей точки O.
Чтобы найти вектор-разность, нужно
к
из
общей точки O.
Чтобы найти вектор-разность, нужно
к ![]() добавить
вектор
добавить
вектор ![]() или
или ![]() .
Тогда
.
Тогда ![]() .
Вектор
.
Вектор ![]() ,
соединяющий концы векторов
,
соединяющий концы векторов ![]() и
и ![]() и
направленный от "вычитаемого" к
"уменьшаемому" (т.е. от второго
вектора к первому), и будет разностью
и
направленный от "вычитаемого" к
"уменьшаемому" (т.е. от второго
вектора к первому), и будет разностью ![]() .
Действительно, по правилу сложения
векторов
.
Действительно, по правилу сложения
векторов ![]() или
или ![]() .
.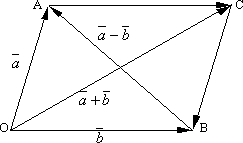
Таким
образом, если на векторах ![]() и
и ![]() ,
отложенных из общей точки O,
построить параллелограмм OACB,
то вектор
,
отложенных из общей точки O,
построить параллелограмм OACB,
то вектор ![]() ,
совпадающий с одной диагональю
параллелограмма, равен сумме
,
совпадающий с одной диагональю
параллелограмма, равен сумме ![]() ,
а вектор
,
а вектор ![]() ,
совпадающий с другой диагональю, равен
разности
,
совпадающий с другой диагональю, равен
разности ![]() .
.
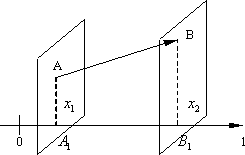
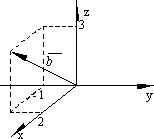
Проекция вектора на ось
|
усть в пространстве
даны два вектора
Рассмотрим
ось l и
отложим на ней единичный вектор
Под углом между
вектором
Итак, пусть l –
некоторая ось и Обозначим через A1 и B1 проекции на ось lсоответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l.
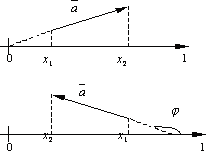
Тогда проекцией вектора
Проекцию
вектора
Ясно, что если
угол между вектором
Таким образом,
проекция вектора Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор. Рассмотрим некоторые основные свойства проекций.
Доказательство.
Ясно, что проекция вектора не изменится
при его параллельном переносе, поэтому
достаточно рассмотреть случай, когда
начало вектора совпадает с началом
отсчёта O оси l.
Так как координата проекции начала
равна нулю, то обозначим
Доказательство.
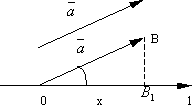
Пусть Это свойство можно обобщить на случай любого числа слагаемых.
Доказательство.
Пусть угол между вектором
Если λ > 0, то
вектор
При λ > 0
Если же λ < 0,
то Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось. |
|
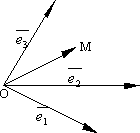
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим
несколько векторов ![]() .
.
Линейной
комбинацией данных
векторов называется любой вектор вида ![]() ,
где
,
где ![]() -
некоторые числа. Числа
-
некоторые числа. Числа ![]() называются
коэффициентами линейной комбинации.
Говорят также, что в этом случае
называются
коэффициентами линейной комбинации.
Говорят также, что в этом случае ![]() линейно
выражается через данные векторы
линейно
выражается через данные векторы ![]() ,
т.е. получается из них с помощью линейных
действий.
,
т.е. получается из них с помощью линейных
действий.
Например,
если даны три вектора ![]() то
в качестве их линейной комбинации можно
рассматривать векторы:
то
в качестве их линейной комбинации можно
рассматривать векторы: ![]()
Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.
Векторы ![]() называются линейно
зависимыми,
если существуют такие числа
называются линейно
зависимыми,
если существуют такие числа![]() ,
не все равные нулю, что
,
не все равные нулю, что ![]() .
Ясно, что заданные векторы будут линейно
зависимыми, если какой-либо из этих
векторов линейно выражается через
остальные.
.
Ясно, что заданные векторы будут линейно
зависимыми, если какой-либо из этих
векторов линейно выражается через
остальные.
В
противном случае, т.е. когда
соотношение ![]() выполняется
только при
выполняется
только при ![]() ,
эти векторы называются линейно
независимыми.
,
эти векторы называются линейно
независимыми.
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство:
-
Действительно, пусть имеем два коллинеарных вектора
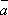 и
и 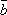 .
Тогда либо оба они равны нулю, и
следовательно, любая их линейная
комбинация
.
Тогда либо оба они равны нулю, и
следовательно, любая их линейная
комбинация 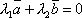 при
любых λ1 и
λ2,
либо один из них не нуль, тогда другой
отличается от него на числовой множитель,
например,
при
любых λ1 и
λ2,
либо один из них не нуль, тогда другой
отличается от него на числовой множитель,
например, 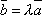 .
Но отсюда
.
Но отсюда 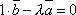 ,
а это и означает линейную зависимость
векторов
,
а это и означает линейную зависимость
векторов 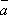 и
и 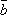 .
. -
Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы
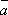 и
и 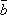 линейно
зависимы. Тогда найдутся числа λ1 и
λ2 такие,
что
линейно
зависимы. Тогда найдутся числа λ1 и
λ2 такие,
что 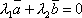 ,
причём, например, λ2 ≠
0. Тогда
,
причём, например, λ2 ≠
0. Тогда 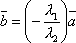 ,
т.е. векторы коллинеарны.
,
т.е. векторы коллинеарны.
Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны.
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство.
-
Пусть три вектора
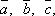 линейно
зависимы, т.е.
линейно
зависимы, т.е. 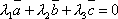 ,
где, например, λ3 ≠
0. Тогда
,
где, например, λ3 ≠
0. Тогда 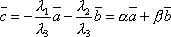 .
.
Отнесём
векторы ![]() и
и ![]() к
одному началу и проведём через них
плоскость. Тогда
к
одному началу и проведём через них
плоскость. Тогда ![]() и
и ![]() будут
лежать в той же плоскости, а потому и их
сумма, т.е.
будут
лежать в той же плоскости, а потому и их
сумма, т.е. ![]() будет
лежать в той же плоскости, т.е.
будет
лежать в той же плоскости, т.е. ![]() –
компланарны.
–
компланарны.
-
Пусть теперь векторы
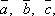 –
компланарны. Тогда они будут лежать в
одной плоскости. Отнесём все три вектора
к одному началу.
–
компланарны. Тогда они будут лежать в
одной плоскости. Отнесём все три вектора
к одному началу.
Если
векторы ![]() и
и ![]() не
коллинеарны, то очевидно, вектор
не
коллинеарны, то очевидно, вектор ![]() можно
предствить в виде
можно
предствить в виде ![]() .
Действительно из рисунка видно, что
.
Действительно из рисунка видно, что ![]() ,
где
,
где ![]() и
и ![]() ,
а значит найдутся числа
,
а значит найдутся числа ![]() и
и ![]() такие,
что
такие,
что ![]() .
.
Если
же вектор ![]() коллинеарен
вектору
коллинеарен
вектору ![]() ,
то один из них линейно выражен через
другой, т.е.
,
то один из них линейно выражен через
другой, т.е. ![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.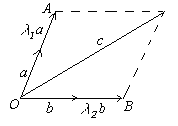
Таким образом, три некомпланарных вектора всегда линейно независимы. Кроме того, можно показать, что каждые четыре вектора линейно зависимы.
БАЗИС
Базисом называется
совокупность отличных от нулей линейно
независимых векторов. Элементы базиса
будем обозначать ![]() .
.
В предыдущем пункте мы видели, что два неколлинеарных вектора на плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть
в пространстве задан базис ![]() .
Тогда любой вектор
.
Тогда любой вектор ![]() можно
представить в виде линейной комбинации
можно
представить в виде линейной комбинации ![]() ,
где x, y, z –
некоторые числа. Такое разложение
единственно.
,
где x, y, z –
некоторые числа. Такое разложение
единственно.
Доказательство.
-
Докажем сначала существование такого представления.
-
Предположим, что
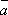 коллинеарен
какому-либо из векторов базиса,
например,
коллинеарен
какому-либо из векторов базиса,
например, 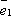 .
Тогда по доказанному выше
.
Тогда по доказанному выше 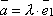 .
Следовательно,
.
Следовательно, 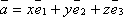 ,
где x =
l, y = z =
0.
,
где x =
l, y = z =
0.
-
Пусть
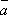 компланарен
с какой-либо парой базисных векторов,
например, с
компланарен
с какой-либо парой базисных векторов,
например, с 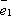 и
и 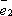 .
Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам
.
Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам 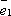 и
и 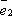 .
Тогда
.
Тогда  ,
причём векторы
,
причём векторы 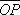 и
и 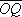 коллинеарны
соответственно векторам
коллинеарны
соответственно векторам  и
и 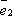 .
Поэтому найдутся числа x и y такие,
что
.
Поэтому найдутся числа x и y такие,
что 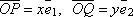 ,
а значит
,
а значит 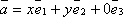 .
. -
Пусть
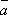 некомпланарен
ни с одной парой базисных векторов.
Отложим
некомпланарен
ни с одной парой базисных векторов.
Отложим 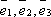 от
одной точки и проведём через конец
вектора
от
одной точки и проведём через конец
вектора 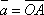 прямую,
параллельную вектору
прямую,
параллельную вектору 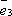 .
Она пересечёт плоскость
.
Она пересечёт плоскость 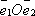 в
точке A1.
Очевидно, что
в
точке A1.
Очевидно, что 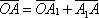 .
Но вектор
.
Но вектор 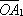 компланарен
векторам
компланарен
векторам 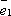 и
и 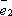 ,
следовательно, по доказанному выше,
,
следовательно, по доказанному выше, 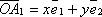 ,
а вектор
,
а вектор 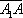 коллинеарен
коллинеарен 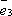 ,
поэтому
,
поэтому 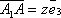 .
Таким образом,
.
Таким образом, 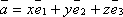 .
.
-
-
Докажем теперь единственность такого представления.
Допустим,
что возможны два представления
вектора ![]() и
и ![]() .
Причём, например,
.
Причём, например, ![]() .
Тогда должны иметь
.
Тогда должны иметь ![]() ,
т.к. иначе мы имели бы две прямые,
проходящие через точку A1 параллельно
,
т.к. иначе мы имели бы две прямые,
проходящие через точку A1 параллельно ![]() .
Из последнего равенства вытекает, что
.
Из последнего равенства вытекает, что ![]() .
Получили противоречие с нашим
предположением, что и доказывает теорему.
.
Получили противоречие с нашим
предположением, что и доказывает теорему.
В качестве частного случая из этой же теоремы можно сформировать следующее утверждение:
Если
задан базис ![]() на
плоскости, то любой вектор, компланарный
с векторами
на
плоскости, то любой вектор, компланарный
с векторами ![]() можно
представить в виде
можно
представить в виде ![]() ,
причём такое разложение единственно.
,
причём такое разложение единственно.
Таким
образом, базис позволяет однозначно
сопоставить каждому вектору тройку
чисел – коэффициенты разложения этого
вектора по векторам базиса: ![]() .
Верно и обратное, каждой тройке чисел x,
y, z при
помощи базиса можно сопоставить вектор,
если составить линейную комбинацию
.
Верно и обратное, каждой тройке чисел x,
y, z при
помощи базиса можно сопоставить вектор,
если составить линейную комбинацию ![]() .
.
Если ![]() базис
и
базис
и ![]() ,
то числа x,
y, z называются координатами вектора
,
то числа x,
y, z называются координатами вектора ![]() в
данном базисе. Координаты
вектора
в
данном базисе. Координаты
вектора ![]() обозначают
обозначают ![]() .
.
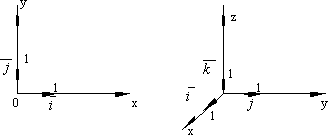
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
|
Пусть в пространстве
задана точка O и
три некомпланарных вектора Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки. Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в
выбранной системе координат произвольную
точку M.
Введём понятие координаты точки M.
Вектор
Вектору Координаты радиус-вектора точки M. называются координатами точки M. в рассматриваемой системе координат. M(x,y,z). Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой. Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату. Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы,
взятые в качестве базиса, в выбранной
системе координат, имеют единичную
длину и попарно перпендикулярны, то
система координат называется декартовой
прямоугольной системой
координат. В этом случае основные
векторы принято обозначать буквами
Таким образом,
любой вектор в декартовой прямоугольной
системе координат можно записать в
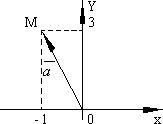
виде: Примеры.
М(-1;3).
В дальнейшем мы в основном будем использовать только декартову прямоугольную систему координат. |
|
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Пусть
в декартовой прямоугольной системе
координат задан вектор ![]() .
Направление вектора в пространстве
определяется углами α, β, γ которые
вектор составляет с осями координат.
Косинусы этих углов cos α, cos β, cos γ
называются направляющими
косинусами вектора.
.
Направление вектора в пространстве
определяется углами α, β, γ которые
вектор составляет с осями координат.
Косинусы этих углов cos α, cos β, cos γ
называются направляющими
косинусами вектора.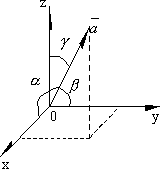
Найдем выражение для направляющих косинусов вектора.
Пусть
вектор задан в координатной форме ![]() .
.
Тогда ![]() ,
откуда
,
откуда .
.
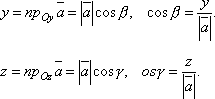
Несложно
показать, что ![]() .
.
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
-
При умножении вектора на число все его координаты умножаются на это число, т.е. если
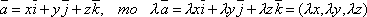 .
.
Действительно, используя свойства операций умножения вектора на число и сложении векторов будем иметь
![]() .
.
При
сложении векторов их соответствующие
координаты складываются, т.е. если ![]() .
.
Доказательство очевидно.
Условие коллинеарности двух векторов в коорднинатной форме.
Два
вектора коллинеарны тогда и только
тогда, когда их соответствующие координаты
пропорциональны. Т.е. если ![]() ,
то
,
то![]() .
.
Доказательство:
-
Пусть вектор
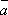 коллинеарен
коллинеарен 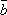 ,
тогда найдется λ такое, что
,
тогда найдется λ такое, что 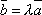 .
Значит,
.
Значит, 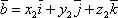 и
и 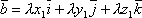 .
Поскольку разложение вектора по
элементам базиса
.
Поскольку разложение вектора по
элементам базиса 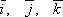 единственно,
то
единственно,
то 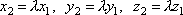 .
. -
Пусть выполняется равенство
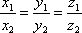 .
Обозначим коэффициент пропорциональности
через λ. Тогда
.
Обозначим коэффициент пропорциональности
через λ. Тогда 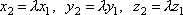 и,
следовательно,
и,
следовательно, 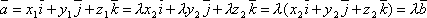 ,
т.е.
,
т.е. 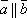 .
Теорема доказана.
.
Теорема доказана.
Пример.
-
Даны векторы
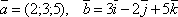 .
Найти вектор
.
Найти вектор 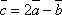 .
.
![]() .
.
-
Найти координаты вектора
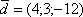 в
базисе, образованном векторами
в
базисе, образованном векторами 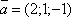 ,
,  ,
,  .
.
Обозначим
координаты вектора ![]() в
новом базисе
в
новом базисе ![]() .
Тогда в новом базисе будем иметь:
.
Тогда в новом базисе будем иметь:
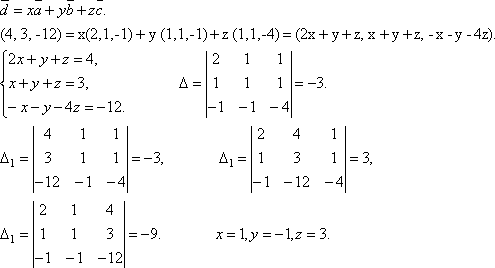
Итак, ![]() .
.
Рассмотрим
две произвольные функцию y=
x3.
Будем рассматривать равенство y= x3 как
уравнение относительно x.
Это уравнение для каждого значения у определяет
единственное значение x: ![]() .
Геометрически это значит, что всякая
прямая параллельная оси Oxпересекает
график функции y=
x3 только
в одной точке. Поэтому мы можем
рассматривать x как
функцию от y.
Функция
.
Геометрически это значит, что всякая
прямая параллельная оси Oxпересекает
график функции y=
x3 только
в одной точке. Поэтому мы можем
рассматривать x как
функцию от y.
Функция ![]() называется
обратной по отношению к функции y=
x3.
называется
обратной по отношению к функции y=
x3.
Прежде чем перейти к общему случаю, введем определения.
Функция y
= f(x) называется возрастающей на
некотором отрезке, если большему значению
аргумента x из
этого отрезка соответствует большее
значение функции, т.е. если x2>x1,
вектора ![]() .
.
Очевидно,
что ![]() .
Но по определению координат вектора
.
Но по определению координат вектора ![]() и
и ![]() .
Следовательно,
.
Следовательно,
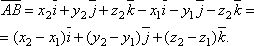
Таким
образом, чтобы найти координаты вектора ![]() ,
нужно из координат его конца вычесть
соответствующие координаты начала.
,
нужно из координат его конца вычесть
соответствующие координаты начала.
Примеры.
-
Заданы точкиA(1; -2; 3), B(2; 0; -1). Найти вектор
 .
.
![]()
-
Даны A(-2; 3; 1), В(-1; 2; 0), С(0; 1; 1). Найти
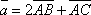 .
.
![]()
![]()
-
Известно, что
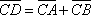 .
Найти координаты точки D,
если
.
Найти координаты точки D,
если
А(3; -4; -1), В(-4; 4; 1), С(-3; -5; 4).
Пусть ![]() тогда
тогда
![]() .
С другой стороны
.
С другой стороны ![]() .
Следовательно, должно выполняться
равенство (x+3; y+5; z-4)=(5;10;-8).
Отсюда
.
Следовательно, должно выполняться
равенство (x+3; y+5; z-4)=(5;10;-8).
Отсюда
x=2, y=5, z=-4, т.е. точка D имеет координаты D(2; 5; -4).
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Мы
рассмотрели умножение вектора на число.
Однако во многих задачах механики и
физики встречается операция умножения
вектора на вектор. Но при этом результат
может быть как числом, так и вектором.
Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.
Пусть
даны два вектора ![]() и
и ![]() ,
угол между, которыми равен
,
угол между, которыми равен ![]() .
.
Скалярным произведением
векторов ![]() и
и ![]() называется
число, равное произведению длин этих
векторов на косинус угла между ними.
Скалярное произведение обозначается
называется
число, равное произведению длин этих
векторов на косинус угла между ними.
Скалярное произведение обозначается ![]() .
Итак,
.
Итак, ![]() .
.
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
-
Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов
 и
и 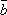
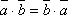 .
.
Очевидно, из определения скалярного произведения:
![]() .
.
-
Для любого числа λ и любых векторов
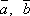 имеем:
имеем:
![]() .
.
Доказательство.
Ограничимся случаем, когда λ > 0. В этом
случае угол между векторами ![]() и
и ![]() совпадает
с углом между векторами
совпадает
с углом между векторами ![]() и
и ![]() ,
, ![]() .
.
Поэтому ![]() .
Откуда
.
Откуда ![]()
Аналогично
доказывается и равенство ![]() .
.
Случай λ <0 рассмотреть самостоятельно.
-
Для любых векторов
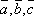 выполняется
равенство
выполняется
равенство 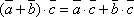 .
.
Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь
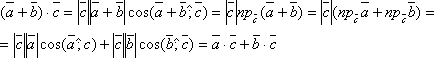
-
Для любого вектора
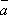 выполняется
соотношение
выполняется
соотношение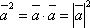 .
.
Действительно,
так как ![]() ,
то
,
то ![]() .
.
Из
этого свойства в частности следует ![]() .
.
-
Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это свойство очевидно из определения скалярного произведения.
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Пример. Дан
вектор ![]() .
Известно, что
.
Известно, что ![]()
Найти ![]() .
.
Имеем![]() ,
т.е.
,
т.е. ![]() .
.
Найдем: ![]()
Следовательно, ![]() .
.
Рассмотрим,
как находится скалярное произведение
векторов, если они заданы в координатной
форме. Пусть даны два вектора ![]() и
и ![]() .
.
Рассмотрим
сначала все возможные скалярные
произведения векторов ![]() друг
на друга.
друг
на друга.
Поэтому

Итак,
скалярное произведение векторов равно
сумме произведений соответствующих
координат: ![]() .
.
Это соотношение позволяет вычислить длину вектора через его координаты:
![]() .
.
Далее
из определения скалярного
произведения ![]() находим
находим
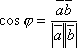 .
.
Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами
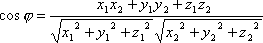 .
.
Условие ортогональности двух векторов:
![]() или
или ![]() .
.
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
Примеры.
-
Пусть А(-1; 1; 0), B(3; 1; -2),
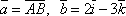 .
Найти:
.
Найти:-
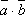 ;
; -
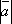 и
и 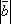 ;
; -
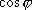 .
.-
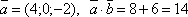 .
. -
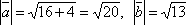 .
. -
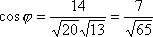 .
.
-
-
-
Найти
 в
в 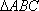 ,
если известны координаты его вершин A(1;
5; 6),
,
если известны координаты его вершин A(1;
5; 6),
B(5;
3; 10), C(2;
1; 14).
![]()
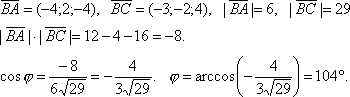
-
При каком значении m векторы
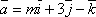 и
и 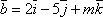 перпендикулярны?
перпендикулярны?
Условие
ортогональности двух векторов ![]() .
.
![]() .
Следовательно, m =
15.
.
Следовательно, m =
15.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Введем
сначала понятие ориентации тройки
векторов.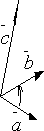

Пусть
даны три некомпланарных вектора ![]() с
общим началом, перечисленных в определенном
порядке: первый –
с
общим началом, перечисленных в определенном
порядке: первый – ![]() ,
второй –
,
второй – ![]() ,
третий –
,
третий – ![]() .
.
Тройка
некомпланарных
векторов ![]() называется правоориентированной или
просто правой,
если из конца третьего вектора кратчайший
поворот от первого ко второму виден
против часовой стрелки. В противном
случае тройку векторов называют левой,
в этом случае если мы будем смотреть с
конца вектора
называется правоориентированной или
просто правой,
если из конца третьего вектора кратчайший
поворот от первого ко второму виден
против часовой стрелки. В противном
случае тройку векторов называют левой,
в этом случае если мы будем смотреть с
конца вектора ![]() ,
то кратчайший поворот от
,
то кратчайший поворот от ![]() к
к ![]() осуществляется
по часовой стрелке.
осуществляется
по часовой стрелке.
Векторным
произведением векторов ![]() и
и ![]() называется
новый вектор
называется
новый вектор ![]() ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
-
Длина вектора
 равна
площади параллелограмма, построенного
на векторах
равна
площади параллелограмма, построенного
на векторах  и
и  .
.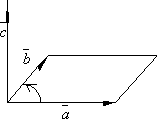
-
Вектор
 перпендикулярен
плоскости этого параллелограмма.
перпендикулярен
плоскости этого параллелограмма. -
Он направлен так, что векторы
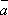 и
и 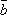 образуют
правую тройку векторов.
образуют
правую тройку векторов.
Векторное
произведение векторов ![]() и
и ![]() обозначается
символом
обозначается
символом ![]() .
Если хотя бы один из сомножителей равен
нулю, то векторное произведение по
определению считают равным нулю
.
Если хотя бы один из сомножителей равен
нулю, то векторное произведение по
определению считают равным нулю
Векторное произведение обладает следующими свойствами:
-
Из определения следует, что длина векторного произведения численно равна площади параллелограмма, построенного на векторах, и, следовательно, находится по формуле:
![]() .
.
Таким
образом, ![]() и
и ![]() .
.
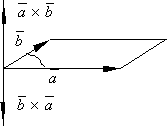
-
При перестановке сомножителей векторное произведение меняет свой знак
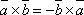 .
.
Действительно
из определения векторного произведения
следует, что векторы ![]() и
и ![]() имеют
одинаковые модули, расположены на одной
прямой, но направлены в противоположные
стороны. Поэтому, векторы
имеют
одинаковые модули, расположены на одной
прямой, но направлены в противоположные
стороны. Поэтому, векторы ![]() и
и ![]() являются
противоположными векторами и поэтому
являются
противоположными векторами и поэтому ![]() .
.
-
Скалярный множитель можно выносить за знак векторного произведения, т.е. для любого числа λ и любых векторов
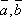
![]() .
.
Доказательство
этого свойства непосредственно следует
из определения векторного произведения.
Докажем для λ > 0. В этом случае ![]() .
Тогда по определению векторного
произведения
.
Тогда по определению векторного
произведения
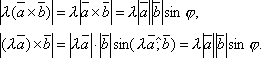
Вектор ![]() перпендикулярен
векторам
перпендикулярен
векторам ![]() и
и ![]() .
Вектор
.
Вектор ![]() также
также ![]() векторам
векторам ![]() и
и ![]() ,
т.к. векторы
,
т.к. векторы ![]() и
и ![]() ,
, ![]() и
и ![]() лежат
в одной плоскости. Следовательно,
векторы
лежат
в одной плоскости. Следовательно,
векторы ![]() и
и ![]() коллинеарны.
Очевидно, что направления их также
совпадают. Т. к.
коллинеарны.
Очевидно, что направления их также
совпадают. Т. к. ![]() ,
и следовательно,
,
и следовательно, ![]() ,
то
,
то ![]() .
.
Поэтому ![]() .
.
Аналогично проводится доказательство для случая λ < 0.
-
Для любых векторов
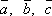 имеет
место равенство
имеет
место равенство
![]() .
.
Примем без доказательства.
-
Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда один из сомножителей равен нулю или векторы коллинеарны.
Действительно,
если векторы коллинеарны, то ![]() ,
т.е. площадь параллелограмма, построенного
на данных векторах,равна нулю.
,
т.е. площадь параллелограмма, построенного
на данных векторах,равна нулю.
Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
В
частности ![]() .
.
Примеры.
-
Раскрыть скобки
![]() .
.
-
Найти площадь треугольника, построенного на векторах
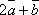 и
и 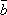 ,
если известно, что
,
если известно, что 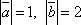 и
и 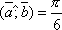 .
.
![]() .
.
Найдем ![]() .
.
![]() .
.
Можно
показать, что если ![]() и
и ![]() ,
то координаты векторного произведения
векторов
,
то координаты векторного произведения
векторов ![]() и
и ![]() находятся
по формуле:
находятся
по формуле:
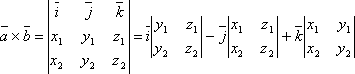 .
.
Примеры.
-
Найти векторное произведение векторов
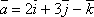 и
и 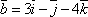 .
.
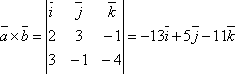 .
.
-
Найти площадь
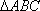 ,
если A(2;
3; 1), B(-1;
-2; 0), C(-3;
0; 1).
,
если A(2;
3; 1), B(-1;
-2; 0), C(-3;
0; 1).
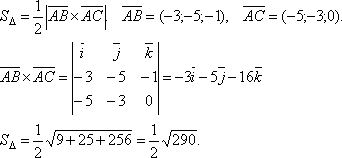
-
Даны векторы
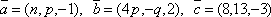 .
Найти параметры n,
p, q если
известно, что векторы
.
Найти параметры n,
p, q если
известно, что векторы 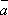 и
и  коллинеарны,
а векторы
коллинеарны,
а векторы 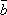 и
и  ортогональны.
ортогональны.
Так
как векторы ![]() и
и ![]() коллинеарны,
то
коллинеарны,
то ![]() .
Векторы
.
Векторы ![]() и
и ![]() ортогональны,
поэтому
ортогональны,
поэтому ![]() .
Итак, получили систему уравнений
.
Итак, получили систему уравнений
![]()
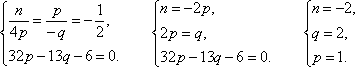

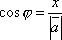 .
Откуда
.
Откуда 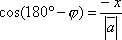 .
Т.е.
.
Т.е.