Вопрос 16: Определение согласованности мнений экспертов.

В случае участия в опросе нескольких экспертов расхождения в их оценках неизбежны. Величина этого расхождения имеет важное значение. Групповая оценка может считаться достаточно надежной только при условии хорошей согласованности ответов отдельных специалистов.

Коэффициент согласованности определяется с помощью коэффициента конкордации (согласия):

1. Дисперсионный коэффициент конкордации: W_Д=Д/Д_max, где Д – дисперсия мнений экспертов, Д_max – максимальное значение дисперсии мнения экспертов. Имеетсяm– экспертов иn– объектов:, где,

r_ij– ранг, присваиваемыйj-м экспертомi-му объекту.

Д_max = m²(n³-n)/ 12(n-1), , Д=S/(n-1)

W= 12S/m²(n³-n), если среди оценок экспертов есть связные ранги, то

, T_j– показатель связных рангов вj-ой ранжировке.

Энтропийный коэффициент конкордации:

W_э= 1-H/H_max,H– энтропия.

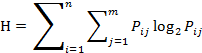,P_ij=m_ij/m,

Коэффициент Wизменяется в диапазоне от 0 до 1. Его равенство единице означает, что все эксперты присвоили объектам одинаковые ранги. Чем ближе значение коэффициента к нулю, тем менее согласованными являются оценки экспертов.

17. Элементы байесовских моделей

Пусть неидеальный эксперимент е не приводит к определению в точности состояний природы П_j, а лишь дает некоторые косвенные сведения в пользу тех или иных состояний. Тогда в общем случае мы можем предположить, что эксперименте приводит к появлению одного из событийВ₁, В₂ ... В_k. Причем вероятности этих событий (исходов эксперимента) зависят от условий, в которых он проводится, т.е.П₁, П₂ ... П_n.

Обозначим условную вероятность появления события Р(В_l/П_j),гдеj= 1...n,l=1...k. Будем считать, что все эти условия вероятности нам известны. После осуществления экспериментае, давшего некоторый исход, нам придется пересмотреть вероятности условий: состояния природы будут характеризоваться не прежними априорными вероятностямиQ₁, Q₂ ... Q_n, а новыми апостериорными (вероятности после опыта)Q₁, Q₂ ... Qn, т.е. условными вероятностямиА₁, А₂ ... An при условии, что эксперимент дал результат В_l

Из курса теории вероятности известно, что апостериорные вероятности подсчитываются по формуле Байеса:

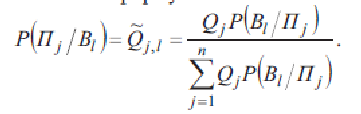
С этой формулой связан подход принятий решений в ситуации неопределенности, называемый байесовским подходом. Иллюстрацией этого подхода принятия решений в условиях неопределенности даже безотносительно игр с природой может быть следующий пример.

Пример оценивания результатов бурения

Испытание керна и другие виды испытаний, производимые разведочной скважиной, не всегда позволяют достоверно определить нефтегазоносность пласта. Пласт может быть вскрыт скважиной в законтурной зоне (зоне вне пласта) или может быть слабо выражен в

области вскрытия. Тогда используют косвенные методы, которые дают результаты, обладающие значительной долей неопределенности, например, микропалеонтологию.

Допустим, экспертиза геологов и результаты предыдущих исследований дали следующие гипотезы:

Р(Н1)=0,6 - пласт нефтеносный;

Р(Н2) = 0,4 - пласт водоносный.

Надо найти условную вероятность того, что пласт нефтеносен, если:

• произошел случай В1 - в керне обнаружена ключевая микрофлора;

• произошел случай В2 - в керне не обнаружена ключевая микрофлора.

Пусть далее известно, что нефтяные и водоносные пласты содержат одинаковую микрофауну, но в нефтеносном пласте она встречается в 95% случаев, а в водоносном - в 70%. Следовательно, нам известна условная вероятность

Р(В1/Н1)=0,95;

Р(В1/Н2)=0,70.

Вероятность открытия месторождения на основании формулы Байеса, после того, как обнаружена микрофлора (в случае В1), определяется по следующей формуле: