41. Дискретные цепи Маркова с дискретным временем

Марковских случайных процессы с дискретным временем нашли применение для прогноза множества показателей, которые меняются щ года в год одновременно, но непосредственно связи между ними не установлены ввиду отсутствия информации или крайней сложности этих связей. Примером может служить прогноз потребностей народного хозяйства в ресурсах. При этом, однако, при реализации данного прогноза устанавливается на перспективу сама структура потребления ресурсов различными отраслями.

Марковский случайный процесс с дискретным временем задается графом состояний элементов системы и матрицей вероятностей Кодов элементов системы из состояния в состояние. Обычно при исследовании такого процесса интересуются вероятностями пребывания системы в j-м состоянии.

Для вычисления вероятности перехода в j-oeсостояниеPj- на к-м шаге существует соотношение Колмогорова - Чепмена:

,

Где – вероятность пребывания элементов системы вj-ом состоянии наk-ом шаге (вk-й дискретный интервал времени),- вероятности перехода системы из состоянияiв состояниеjнаk-м шаге, образующих матрицувероятностей перехода, задаваемую соответствующим графом переходов системы из состояния в состояние.

Переход из состояния в состояние зависит от того, в каком состоянии находилась система на предыдущем шаге и от Рij(K) - матрицы вероятности переходов наk-ом шаге, и эти вероятности могут меняться. Если матрица вероятности переходов не зависит от номера шага, то цепь Маркова называется однородной.

В основе же прогноза лежит вычисление матрицы переходов, элементами которой являются вероятности перехода прогнозируемых параметров из одного состояния в другое, от одного значения к другому.

42. Дискретные цепи Маркова с непрерывным временем

Рассматривают также Марковские цепи с дискретными состояниями и непрерывным временем. В этом случае блуждание системы по своим состояниям описывается матрицей интенсивностей переходов системы из состояния в состояние, а уравнения Колмогорова-Чепмена для определения Pj(k) преобразуются в дифференциальные уравнения относительно производныхp'j(t)

.

При нормирующем условии,

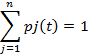
И начальных условиях:

Pi(0)=l;pj(0)=0,j=2,3n.

По определению интенсивность перехода (параметр экспонен­циального закона распределения) имеет размерность 1/t, гдеt - сред­нее время перехода элемента системы из состояния в состояние.

То есть технически, марковскую модель с непрерывным време­нем построить проще, чем модель с дискретным временем, хотя про­блема подчинения пуассоновскому закону распределения всех пото­ков событий, переводящих элементы системы из состояния в состоя­ние, остается. Кроме того, марковские процессы с непрерывным временем позволяют оперировать не только с вероятностями пребы­вания системы в своих состояниях, но и непосредственно с самими элементами (элементами, параметрами) системы. Для этого может быть использован метод динамики средних, элементов, одинаково блуждающим по своим состояниям (например, скважины на нефтегазовом месторождении).

Метод динамики моментов, позволяет описывать функционирование, а, следовательно, и прогнозирование поведения различных технических, организационных и других систем с помощью систем дифференциальных уравнений, аналогичных уравнениям Колмогорова, но записанных, не как обычно, относительно вероятностей пребывания элементов системы в своих состояниях, а относительно средних численностей состояний элементов, а также их дисперсий и корреляционных моментов (для метода динамики моментов).

Метод разработан в предположении, что все потоки событий, переводящие отдельные элементы из состояния в состояние - пуассоновские, тогда динамика поведения элемента, а, следовательно, и всей системы в целом, описывается марковским случайным процессом.

Обычно метод динамики средних применяется там, где система имеет большое количество однородных элементов и состояний. При этом под однородностью элементов понимается, прежде всего, их идентичность относительно интенсивностей переходов из состояния в состояние и идентичность самих этих состояний. В связи с чем, граф состояний системы полностью описывается графом состояния одного элемента.

Система дифференциальных уравнений динамики средних для определения средних численностей состояний элементов Mj[t], в общем виде записывается следующим образом:

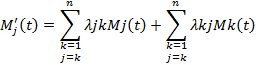
при нормирующем условии,

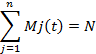
и начальных условиях:

Mi(0)=N; Mj(0)=0, j=2,3,……n.

В этом случае дисперсия D/t) определяется следующим образом:

Dj(t) = Mj(t)(1-(Mj(t)/N)). Выражения для корреляционных функций получено только для случайных процессов типа гибели размножения.

Марковская цепь обладает еще одним свойством. Она может иметь стационарный режим. Стационарность режима работы цепи Маркова состоит в том, что вероятности пребывания системы в каком-либо состоянии перестают зависеть от номера шага (времени), на котором рассматривается эта цепь, то есть Pj=const(а часто и средние численности состояний в методе динамики средних). В этом случае уравнения Колмогорова-Чепмена преобразуются в систему линейных алгебраических уравнений.

Управляемые цепи Маркова

При анализе марковских цепей часто к рассмотрению вероятность пребывания системы в различных состояниях в различные периоды времени добавляют информацию, касающуюся вознаграждения (или наоборот, затрат, расходов), которые могут быть получены при переходах. В этом случае речь идет об управляемых марковских процессах.

Под управляемыми Марковскими процессами понимают такие процессы, у которых имеется возможность до определенной степени управлять значениями переходных вероятностей и влиять, таким образом, на возможные получаемые доходы. В качестве примеров таких процессов можно привести любые торговые операции, у которых вероятность сбыта и получения эффекта может зависеть от рекламы, мероприятий по улучшению качества, выбора покупателя или рынка сбыта и т.д.

Формально, управляемой цепью Маркова (УЦМ) называется случайный процесс, обладающий марковским свойством и включающий в качестве элементов математической модели конструкцию (кортеж) < Ki,,>.Решение, принимаемое в каждый конкретный момент (шаг процесса) назовем частным управлением.

Таким образом, процесс функционирования системы описываемой УЦМ, выглядит следующим образом:

-если система находится в состоянии i ϵ S и принимается решение k ϵ Кi,то она получает доход;

-состояние системы в последующий момент времени (шаг) определяется вероятность , то есть вероятность того, что система из состоянияiϵSперейдет в состояниеjϵS, если выбрано решениеKi.

Очевидно, общий доход за n-шагов является случайной величиной, зависящей от начального состояния системы и качества принимаемых в течение хода процесса принятия решений, причем это качество оценивается величиной среднего суммарного дохода (при конечном времени) или среднего дохода за единицу времени (при бесконечном времени). В этих двух случаях для нахождения оптимальных решений обычно сводится в первом случае к решению задач динамического стохастического программирования - рекуррентный алгоритм нахождения оптимального решения, а во втором к решению задач линейного программирования - итерационный алгоритм.