39. Марковская модель согласования решений.

При создании математических моделей согласования решений должны фигурировать следующие компоненты

- конечное множество решений (альтернатив) K_i , стратегий, гдеiϵS– номер состояния системы:

- матрици переходов П_[s], соответствующие тому или иному принятию к- решению

- матрицы доходов (расходов) R_[s], также отражающее эффективность данного решения

Формально, управляемой цепью Маркова (УЦМ) называется случайный процесс, обладающий марковским свойством и включающий в качестве элементов математической модели конструкцию (кортеж) < K_i, П_[s],R_[s]>. Решение, принимаемое в каждый конкретный момент (шаг процесса) назовем частным управлением.

Таким образом, процесс функционирования системы описы­ваемой УЦМ, выглядит следующим образом:

-если система находится в состоянии i ϵS и принимается решениеk ϵ К_i то она получает доход r_i;

-состояние системы в последующий момент времени (шаг) определяется вероятностью P_ij , то есть вероятность того, что сис­тема из состоянияI€S перейдет в состояниеj ϵ S, если выбрано решениеK_i.

Очевидно, общий доход за n-шагов является случайной вели­чиной, зависящей от начального состояния системы и качества принимаемых в в течение хода процесса принятия решений, причем это качество оценивается величиной среднего суммарного дохода (при конечном времени) или среднего дохода за единицу времени (при бесконечном времени). В этих двух случаях для нахождения опти­мальных решений обычно сводится в первом случае к решению за­дач динамического стохастического программирования - рекуррент­ный алгоритм нахождения оптимального решения, а во втором к ре­шению задач линейного программирования - итерационный алго­ритм.

40. Цепи Маркова – основные положения

Марковские случайные процессы названы по фамилии русского математика Маркова. Теория Марковских случайных процессов имеет наглядный и простой математический аппарат.

Дискретная цепь Маркова задастся ориентированным графом (пример которого дан ив рис), в котором вершины ость состояния описываемой системы, а дуги графа для дискретного времени есть вероятности перехода из состояния в состояние. Для непрерывного времени интенсивности перехода, которое обычно задано, искомыми являются вероятности пребывания системы в некотором состоянии.

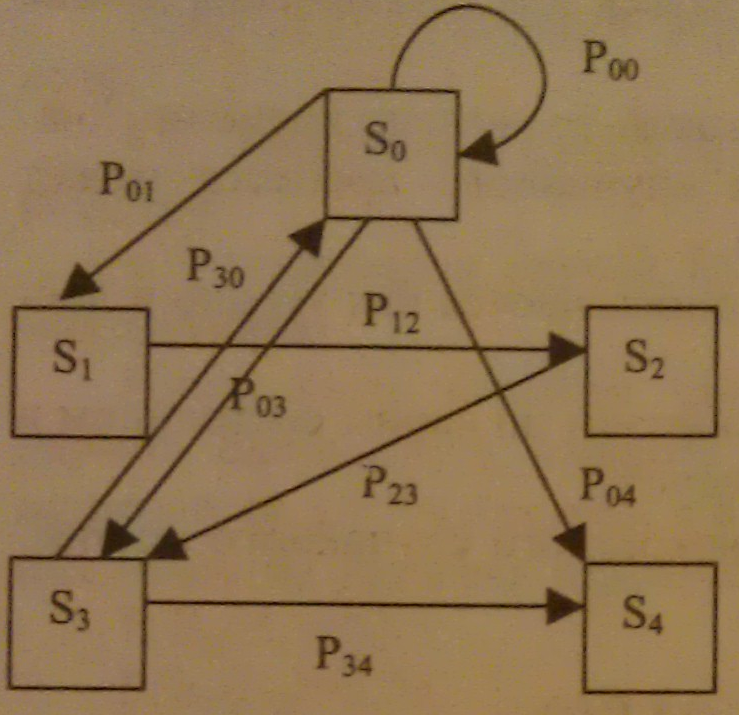
Стрелками обозначается переход системы из одного состояние в другое. Рij— вероятность перехода системы изi-го состояния вj-е.

Одной из основных моделей случайных процессов, используемой я прогнозировании является модель марковских цепей. Такими моделями, которые могут быть включены в системы поддержки принятия решений, описывается большое количество физических, биологических, экономических, технических и других явлений. Применительно к нефтяной и газовой промышленности - это процессы технического обслуживания и ремонта нефтяных и газовых скважин, объектов транспорта нефти и газа, оборудования нефте-(газо)перерабатывающих заводов; процессы планирования и организации проведения геолого-технических мероприятий и геофизических исследования скважин, управления запасами и др.

Марковский процесс (для дискретного времени) описывается соотношением:

Pij (k) = P{S(k) = Sj,S(k -1) = Si},

где S(k) - состояние системы на k-оы шаге, a Sj - j-oe состояние системы.

Условия Марковости:

Случайный процесс «блуждания» в системе по своим состояниям является процессом с пуассоновским законом распределения. Он бывает:

• стационарный;

• ординарный (одновременно система не может находиться в двух состояниях);

• без последствий (отсутствие функциональной связи между состояниями).

Марковские цепи применяемые для прогнозирования поведения подобного рода систем можно разделить на две группы. Цепи Маркова с дискретным временем и цепи Маркова с непрерывным временем.