38. Простейшие алгоритмы согласования решений (согласование в среднем, согласование по Парето, метод идеальной точки).

Процесс согласования группового решения в группе может осуществляться различными способами, выбор которого зависит от сути решаемой проблемы, установленных формальностей, поведения участников, последовательности высказывания мнений участниками, эмоционального состояния участников и др. Поэтому в общем случае процесс согласования решений является трудной теоретической проблемой.

Задача группового выбора формулируется следующим образом. Имеется проблемная ситуация, для решения которой известно несколько вариантов решения. Группа, принимающая решение, состоит из участников. Каждый участник группы может выбирать варианты решения из множества в соответствии со своими предпочтениями. Для принятия решения группе необходимо найти способ образования, единого группового предпочтения путем согласования индивидуальных предпочтений и выбора варианта, устраивающего всех участников решения. Среди групп участников решения могут быть подгруппы с совпадающими целями - предпочтениями, которые можно назвать коалициями. В них может входить от 1 участника до группы из всех участников. Каждая коалиция может иметь свое предпочтение.

Выбор принципа согласования производится на основе характера отношений между ними. Основными типами отношений между коалициями могут быть отношения статус-кво, конфронтация, рациональность. При отношении статус-кво коалиции стараются сохранить существующее положение. Это отношение определяется взаимодействиями слабосвязанных участников и характерно для «экономических структур и организаций. Сильные взаимодействия определяют отношения конфронтации и рациональности.

В случае конфронтации коалиции действуют так, чтобы принести ущерб друг другу.

При рациональных отношениях коалиции действуют в собственных интересах для получения максимального результата, что не обязательно приносит ущерб другим коалициям. Одна коалиция в силу предположения о рациональном поведении другой коалиции может предсказать поведение другой коалиции. В практике существуют несколько принципов согласования вариантов решений в группе.

Метод Парето

Он широко ис­пользуется при ранжировании вариантов решений, объектов и т.п. Состояние А (множество параметров) называется Парето-оптимальным, если не существует другого со­стояния В (множества других параметров) доминирующего состоя­ние А относительно целевой функции. Состояние А доминирует со­стояние В, если хотя бы по одному параметру А лучше В, а по ос­тальным не хуже.

Применительно к задаче переговоров этот принцип утверждает что, если для ситуации В существует такая ситуация А, что выиг­рыш каждого из участников переговоров при реализации ситуации А не меньше, чем при реализации ситуации В и, по крайней мере, один переговорщик получит выигрыш строго больший, то они предпочтут ситуацию А ситуации В.

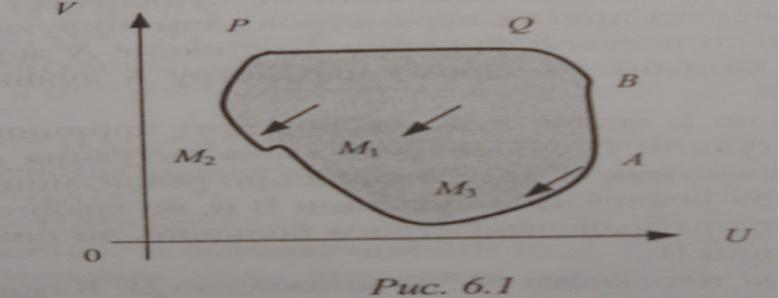
Рассмотрим на плоскости (U, V) множество ω. Каждая его точка обладает одним из следующих свойств: либо все точки, ближайшие к ней, принадлежат множеству ω (такая точка называется внутренней точкой множества ω), либо сколь угодно близко от нее расположены как точки множества, так и точки, множеству не принадлежащие (такие точки называются граничными точками множества). Множе­ство всех граничных точек множества называется его границей. Гра­ничная точка может как принадлежать множеству, так и не принадле­жать. Здесь рассмотрим только такие множества, которым принадле­жат все точки границы.

Точки множества со можно разбить на три класса:

1 класс - точки, которые, оставаясь во множестве со, можно сдви­нуть так, чтобы одновременно увеличились обе координаты (в этот класс попадают все внутренние точки множества ω и часть его гра­ничных точек) (на рис. 6.1 это точкиMl, М2 и МЗ);

2 класс — точки, перемещением которых по множеству со можно увеличить только одну из координат при сохранении значения второй (вертикальный отрезок АВ и горизонтальный отрезокPQна границе множества ω);

3 класс - точки, перемещение которых по множеству со способ­но лишь уменьшить либо одну из координат, либо обе(дугаBQгра­ницы множества ω).

Множество точек третьего класса называется множеством Парето или границей Парето данного множества ω .

Метод идеальной точки

Рассмотрим один из методов, использующий множество Парето - метод идеальной точки. Пусть у нас есть некоторое множество е, каждая точка которого описывается двумя функциям U=Ф(х;у) иV⁼Р(х;y)/).(UиV- средние выигрыши игроков А и В соответственно,axиy - вероятности вы­бора стратегий для получения этого выигрыша).

Теперь в данном множестве ε попытаемся найти такую точку, в которой обе функции U иV принимают свои максимальные значе­ния. В общем случае эта точка окажется вне множества ε. То есть, не существует стратегий, при которых оба игрока получат максималь­ный для каждого выигрыш. Точка, в которой функцииUиV достигают своих максимальных значений, называетсяточкой утопии.

Поэтому строится множество Парето и на нем ищется точка, бли­жайшая к точке утопии — идеальная точка (см. рис. 6.2).

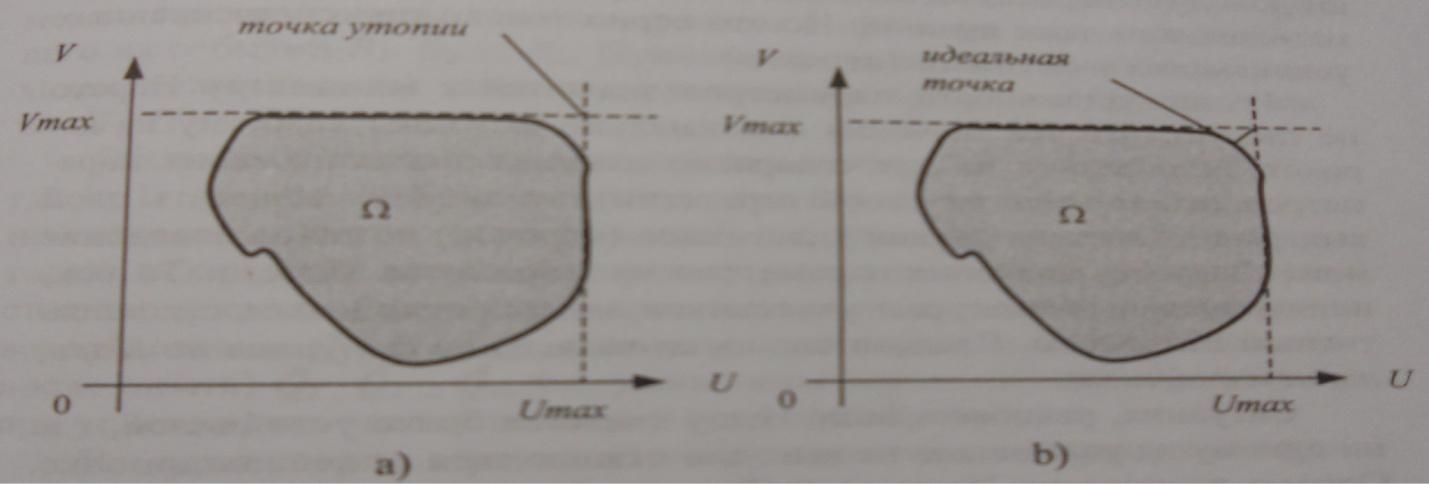
Значения функций U иV в идеальной точке и есть оптимальные средние выигрыши для каждого игрока.