30. Метод идеальной точки.

Рассмотрим один из методов, использующий множество Парето - метод идеальной точки.

Пусть у нас есть некоторое множество е, каждая точка которого описывается двумя функциям U=Ф(х;у) иV=Ψ(х;у) (UиV- средние выигрыши игроков А и В соответственно, а х и у - вероятности выбора стратегий для получения этого выигрыша).

Теперь в данном множестве е попытаемся найти такую точку, в которой обе функции UиVпринимают свои максимальные значения. В общем случае эта точка окажется вне множества е. То есть, не существует стратегий, при которых оба игрока получат максимальный для каждого выигрыш.

Точка, в которой функции UиVдостигают своих максимальных значений, называетсяточкой утопии.

Поэтому строится множество Парето и на нем ищется точка, ближайшая к точке утопии - идеальная точка(см. рис.).

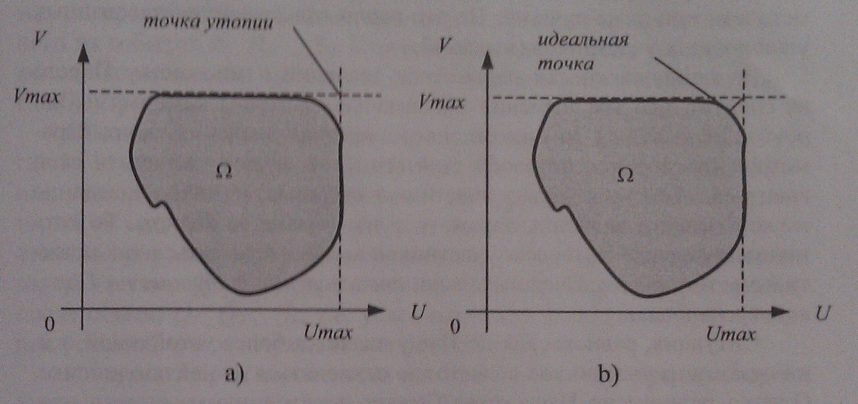
Значения функций UиVв идеальной точке и есть оптимальные средние выигрыши для каждого игрока.

Пусть Н_A(р, q) и Нв (р, q) — средние выигрыши игроков А и В с платежными матрицами

Ситуация (p*q*) в биматричной игре А и В называется оптимальной по Парето, если из того, что

вытекают равенства:

Р =Р*, q=q*.

То есть, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш одного из игроков, не уменьшив при этом выигрыш другого.

31. Метод последовательных уступок.

Руководитель устанавливает СППР (Система поддержки принятия решений) порядок приоритета логических функций, ставя на первое место наиболее важную, и СППР выполняет сл. операции:

СППР находит =, где-значение логической функции по самой важной характеристике, ее индексi=1,j- номер альтернативы.

Руководитель определяет величину уступки

СППР в пределах уступки находит=

Если таких вариантов нет – руководитель увеличивает уступку и в ее пределах СППР выбирает вариант, имеющий максимум по третьей логической функции и.т.д до полного перебора всех .

Такой способ построения компромиссного решения имеет то преимущество, что руководитель имеет возможность наглядно видеть цену (уступки) по каждому критерию.

Процедура получения компромиссного решения может быть реализована и без назначения уступок . В этом случае вначале отбирают варианты решений по первому (наиболее важному) критерию, затем среди отобранных решений выбираются наилучшие решения по второму критерию и.т.д. Процедура завершается при выборе наилучшего решения по последнему критерию.

Если же методом последовательных уступок решается многокритериальная оптимизационная задача, то к исходным ограничениям задачи на каждом шаге добавляются ограничения вида:

32. Алгоритм построения Парето оптимального решения.

Парето-оптимальность – общее понятие равновесия, которое полностью зависит от того, какие элементы в нее включаются. Находя оптимальную точку, все участники переговоров получают доход не меньший, чем при выборе этой точки другим методом, или даже лучший.

Рассмотрим отношение ≥ (>) между оценками х, у ϵ Х: х≥ у (х>у), если Ui(х)>Ui(у) (Ui(х)>Ui(у)) дляi= 1,n. Здесь Ui(x) - функция полезности (предпочтения). Оценка х° ϵ X называется максимальной по ≥ (по >) относительно X, если не существует оценки х ϵ Х такой, что х ≥ х°(х > х°). Оценка максимальная по ≥ называется эффективной, а такжеПарето-оптимальной. То есть, вектор х ϵ X Парето-оптимален тогда и только тогда, если не существует другого х ϵ X такого, что Ui (х) ≥ Ui(х*) дляi= 1,nи строгое неравенство Uj(х) > Uj(х*) выполняется, хотя бы для одногоj.

Множество всех Парето-оптимальных решений образуют рубеж Парето или, что тоже рубеж эффективности. Эти два термина используются в литературе как синонимы.

Оценка максимальная по > называется слабо эффективной, а также слабо оптимальной по Парето или оптимальной по Слейтеру. Множество всех таких оценок на X называется слабо эффективным.

Важным свойством метода Парето является возможность «выбраковывать» из множества возможных решений X заведомо неудачные, уступающие другим по всем критериям.

Из определения Парето-оптимальности следует простой переборный алгоритм нахождения множества Парето-оптимальных элементов. Поскольку Парето-оптимальность определяется не абсолютными, а относительными значениями оценок объектов (вариантов решений) по значениям их параметров, то для реализации алгоритма достаточно иметь информацию о типе отношений между каждой парой объектов, т.е. знать существует ли между ними отношение строгого предпочтения или нет. Поэтому введем булеву переменную

В табл. представлены экономическая и технологическая эф­фективности различных рассмотренных в [9.4] методов воздействия на пласт с целью повышения его нефтеотдачи.

№	Метод	Себестои	Уде льн.	Прирост	Конечная
	воздейст	мость 1м	Кап. Затра-	нефтеотдачи	нефтеотдача
	вия	доп. добыт, нефти, долл. США	ты, тыс. долл. США На (м3 /сут.)	%	%
1	Горение	63- 157	50-157	10-30	45-50
2	Пар	63-119	50-157	15-35	45-50
3	Нагнетание С02	63 - 189	63-157	8-20	55-60
4	Поверхно­стно-активные вещества (ПАВ)	126-314	94-189	12-30	45-50
5	Полимеры	63 - 157	63 - 189	2-10	45-50

Здесь неопределенность выражается разницей в максимальном и минимальном эффекте в зависимости от применяемого метода воз­действия.

Будем сравнивать методы воздействия на пласт по четырем по­казателям, показанным в табл. 9.6. При нахождении величины aij показатели можно сравнивать по средним значениям или по положению интервала значений на числовой оси, считая, например, что показатель "себестоимость 1 м " в интервале 63-119, лучше этого же показателя в интервале 63-157. Для сравнения методов воздействия СППР строит табл. 9.7, не показывая ее руководителям.

Таблица 9.7

№	1	2	3	4	5
1	0	0	0	0	1
2	1	0	0	1	1
3	0	0	0	0	0
4	0	0	0	0	0
5	0	0	0	0	0

В соответствии с табл. 9.7 лучшими методами (1 ранга) оказа­лись "пар" и "нагнетание С0₂". Вычеркивая столбцы и строкиKeKs2 и 3, получаем табл. 9.8.

Таблица 9.8

№	1	4	5
1	0	0	1
4	0	0	0
5	0	0	0

В соответствии с табл. 9.8 методами второго ранга оказались «горение» и «поверхностно-активные вещества». Наконец, самым худшим методом (3 ранга) оказались «полимеры».

В результате ранжирования по Парето система высвечивает на дисплее табл. 9.9.

Таблица 9.9

Ранг	Метод воздействия на пласт
1	Пар
1	Нагнетание СОг
2	Горение
2	Поверхностно-активные вещества
3	Полимеры

Исходя из этих оценок, руководитель выбирает метод воздейст­вия на пласт.