24. Нечеткие числа: виды нечетких чисел; операции над нечеткими числами.

Нечеткой величиной называется произвольное нечеткое множеcтво заданное на множестве действительных чисел R¹:

Нечетким числом называется нечеткая величина, функция принадлежности которой является выпуклой и унимодальной.

Нечеткие числа широко используются в повседневной жизни. Когда мы говорим: «приблизительно три», «приблизительно двадцать пять» и т. п., то тем самым предполагаем использование нечеткого числа. Формально нечеткое число можно рассматривать как нечеткое множество, заданное на множестве действительных чисел и обладающее некоторыми дополнительными свойствами.

Нечеткие числа во многих случаях применяются для непосредственных расчетов (см. например, расчеты чистого дисконтированного дохода, внутренней нормы рентабельности проекта разработки нефтегазового месторождения и др.). При этом, наиболее популярными и легко интерпретируемыми руководителями являются нечеткие числаLR -типа.

Нечеткие числа (L-R)-типа - это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.

Нечеткое число ã, называется нечетким числом LR-типа или LR-числом, если

где a - мода нечеткого числа LR-типа,α - левый коэффициент нечеткости,β - правый коэффициент нечеткости,L(x) - левая функция принадлежности,R(x) - правая функция принадлежности.

Символически число LR-типа, записываются следующим образом:

Арифметические операции над нечеткими числами LR-типа выполняются по следующим правилам. Пусть имеется два нечетких числа LR-типа:

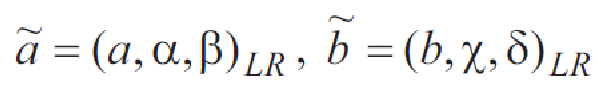
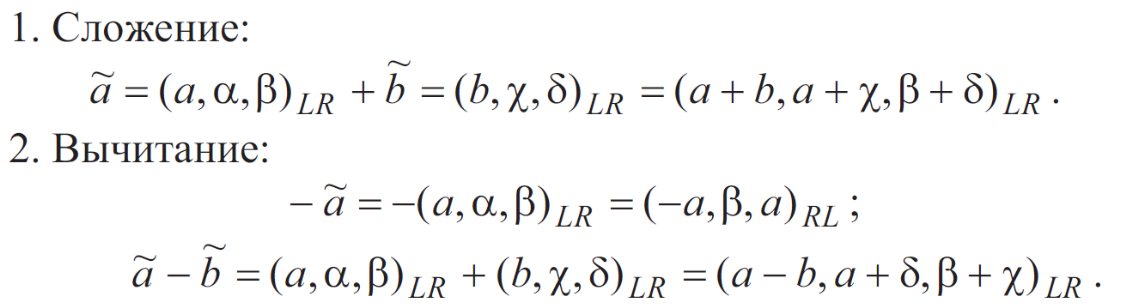
25. Модели нечеткого математического программирования: оптимизация с нечеткими отношениями.

Начало – вопрос №7

Оптимизация с нечеткими отношениями

В общем виде задача нечеткого математического программирования формулируется следующим образом - найти такой вектор x=(xi, x2, ... , xn) , для которого

при ограничениях:

Решение этой задачи ищется на основе следующего подхода.

Пусть Ф₀- значение критерияf(x), достижение которого считается достаточным для выполнения цели, тогда можно ввести некоторыеd иl_i - пороговые уровни, такие, что выполняются неравенства:

которые означают сильное нарушение неравенств

определяющих возможные варианты решения задачи.

При таком подходе возможно для критериев оптимальности и ограничений ввести функции принадлежности решения к допустимому и оптимальному решению. В результате исходная задача оказывается сформулированной в форме задачи достижения нечетко определенной цели при нечетких ограничениях и для ее решения может быть применен подход Белмана-Заде.

К такого рада задачам в силу особенностей нефтегазодобывающего производства можно отнести: планирование геофизических исследований скважин (ГИС), техническое обслуживание и ремонт различных технологических объектов. В общем виде они могут быть записаны в виде следующей оптимизационной задачи

Где x_ij равно 1 - если j -й вид работ (вариант разработки месторождения комплекс ГИС, ТОР и др.) назначается на 1-й вид объектов,

0 - в противном случае.

a_ij^hколичество ресурсов h-го типа, необходимое для проведения j-го вида работ на i-ом виде объектов;

A^h - количество ресурса h-го типа, (время работы МТР, ремонтных бригад, стоимость работ и т.п.), имеющееся в системе;

с­_ij - обобщенная (комплексная) эффективность применения j-го вида работ на i-ом виде объектов.

Известно, что четкий вариант задачи (6.1)-(6.5) хорошо решается методом ветвей и границ или с помощью L-алгоритма. При этом лишь некоторое исключение представляет собой задача распределения ГИС и ТОР по плановым периодам, имеющая в своем составе отличный от (6.1) вид критерия оптимальности, особенность которого состоит в том, что заранее, до начала решения задачи невозможно иметь значения Cij (они вычисляются в ходе решения задачи).

Однако, для всех перечисленных в начале этого раздела задач общими характерными моментами является то, что: 1) правые части ресурсных ограничений представляют собой некоторые средние значения полученные, например, в результате применения моделей теории массового обслуживания; 2) значения коэффициентов C_ij, тоже, как правило, носят качественный (приближенный) характер и получаются в результате качественного экспертного анализа). Поэтому здесь имеется три альтернативных подхода для выбора методов (алгоритмов) решения этих задач.

Первый подход основан на том, что значения коэффициентов a_ij^h,A^h, с­_ij считаются хорошо определенными и для решения задачи применяются упомянутые выше метод "ветвей и границ" илиL-алгоритм .

Второй подход основан на том, что a_ij^h,A^h, с­_ij имеют статистическую неопределенность. Тогда задача (6.1)-(6.5) становится М-задачей стохастического математического программирования, методы и трудности решения которой также хорошо известны. Наконец, третий подход может быть основан на том, что неопределенность коэффициентов с­_ij в большей степени связана с не достаточностью информации и не носит ярко выраженной статистической неопределенности. В свою очередь можно допустить, так же, что при решении задачи (6.1)-(6.5) ресурсные ограничения могут выполняться лишь с определенной степенью точности, например в пределах среднеквадратического отклонения (или в пределах заданных экспертным путем, что в практической ситуации бывает достаточно часто). Учитывая это, задача (6. 1)-(6.5) может быть интерпретирована как обобщенная распределительная задача с нечетко поставленной целью и ограничениями.