
- •Оглавление
- •Предисловие к тому
- •Список используемых сокращений
- •Раздел 1. ФИЗИЧЕСКИЕ УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
- •Глава 1.1 Время и системы координат
- •1.1.1. Время
- •1.1.2. Системы координат
- •1.1.3. Преобразования между системами координат
- •Глава 1.2. Солнечная система
- •1.2.1. Солнце
- •1.2.2. Планеты
- •1.2.3. Спутники и кольца планет
- •1.2.4. Астероиды и карликовые планеты
- •1.2.5. Объекты пояса Койпера. Кометы
- •Глава 1.3. Физические особенности Земли
- •1.3.1. Гравитационное поле и фигура Земли
- •1.3.2. Атмосфера Земли
- •1.3.3. Магнитное поле Земли
- •1.3.4. Корпускулярная радиация в околоземном космическом пространстве
- •1.3.5. Космический мусор и его характеристики
- •Раздел 2. МЕХАНИКА ПОЛЕТА
- •2.1.1. Способы выведения космических аппаратов на орбиту
- •Глава 2.2. Орбитальное движение
- •2.2.1. Невозмущенное орбитальное движение
- •2.2.1.1. Задача двух тел
- •2.2.1.2. Интегралы и уравнение Кеплера
- •2.2.1.3. Орбитальные элементы
- •2.2.1.4. Определение орбит в задаче двух тел
- •2.2.2. Возмущенное орбитальное движение
- •2.2.2.2. Влияние сжатия и атмосферы Земли на движение ИСЗ
- •2.2.2.3. Баллистические модели движения ИСЗ
- •2.2.4. Баллистические условия полета КА
- •2.2.5. Особые орбиты искусственных спутников Земли
- •2.2.5.1. Геостационарные орбиты
- •2.2.5.6. Критическое наклонение и орбиты типа «Молния»
- •Глава 2.3. Межорбитальные перелеты космических аппаратов
- •2.3.1. Понятие космического перелета. Перелет с конечной тягой, импульсный перелет
- •2.3.2. Реактивная сила. Формула Циолковского
- •2.3.4. Необходимые условия оптимальности перелета
- •2.3.5. Случай центрального ньютоновского гравитационного поля
- •2.3.6. Некоторые импульсные перелеты
- •2.3.7. Перелеты между околокруговыми орбитами
- •2.3.8. Оптимальные перелеты с конечной тягой
- •2.4.1. Управление геостационарной орбитой
- •2.4.2. Поддержание высокоэллиптических орбит
- •2.4.3. Поддержание высотного профиля полета Международной космической станции
- •2.4.4. Поддержание солнечной синхронности круговой орбиты
- •2.4.5. Поддержание стабильности местного времени прохождения восходящего узла круговой ССО
- •2.4.6. Управление высотой и трассой низкой круговой орбиты
- •2.4.7. Разведение спутников на круговой орбите
- •Глава 2.5. Спутниковые системы
- •2.5.1. Спутниковые системы и их баллистическое проектирование
- •2.5.2. Спутниковые системы непрерывного зонального обзора на круговых орбитах
- •2.5.2.1. Спутниковые системы на основе полос непрерывного обзора
- •2.5.2.2. Кинематически правильные спутниковые системы
- •2.5.3. Спутниковые системы периодического зонального обзора на круговых орбитах
- •2.5.3.1. Предпосылки создания современной теории периодического обзора
- •2.5.3.2. Регулярные спутниковые системы
- •2.5.3.3. Элементы маршрутной теории оптимизации спутниковых систем периодического обзора
- •2.5.3.4. Некоторые закономерности оптимальных решений
- •2.5.4. Спутниковые системы непрерывного локального обзора на эллиптических орбитах
- •2.5.5. Управление спутниковыми системами на круговых орбитах
- •Глава 2.6. Лунные и межпланетные траектории
- •2.6.1. Лунные траектории космических аппаратов
- •2.6.2. Траектории полета к планетам, астероидам, кометам
- •Глава 3.1. Типы (классификация) аэродинамических компоновок
- •3.1.3. Многоблочные компоновки с продольным разделением ступеней
- •3.1.4. Многоблочные компоновки с продольным делением ступеней и навесными полезными грузами
- •3.1.5. Выступающие и отделяемые элементы конструкции
- •3.3.1. Экспериментальные методы исследований
- •3.3.3. Аналоговые испытания
- •3.3.4. Численные методы расчета аэродинамических характеристик ракет
- •3.4.1. Ветровое воздействие на ракету при старте и транспортировании. Влияние стартовых сооружений и транспортировочных агрегатов
- •3.4.2. Ветровые нагрузки вблизи земли
- •3.4.3. Местные нагрузки при обтекании стационарным потоком
- •3.4.4. Распределенные аэродинамические нагрузки
- •3.4.5. Статическая устойчивость
- •3.4.6. Аэродинамические характеристики стабилизирующих устройств
- •3.4.8. Разделение ступеней ракет
- •3.4.9. Круговые аэродинамические характеристики тел вращения
- •3.4.11. Аэродинамическое воздействие на полезный груз в процессе отделения створок головных обтекателей
- •3.4.12. Аэродинамика отделяемых ступеней и элементов конструкции. Зоны падения (отчуждения)
- •3.5.3. Влияние струй двигателей на аэродинамические характеристики
- •3.5.4. Аэродинамическое нагружение выступающих элементов конструкции. Методы снижения нагрузок
- •3.5.5. Аэродинамические характеристики блоков многоблочных ракет в процессе их отделения
- •3.6.4. Дренирование элементов конструкции
- •3.6.5. Авиационное транспортирование
- •Глава 3.7. Термостатирование отсеков ракет при наземной подготовке
- •3.7.1. Задачи термостатирования. Ограничения. Методы решения
- •3.8.2. Классификация пусковых установок по их конструктивным схемам
- •3.8.4. Особенности тепловых процессов при старте
- •Глава 3.10. Собственная атмосфера космических аппаратов и ее влияние на функционирование приборов и систем
- •3.10.1. Экспериментальные исследования собственной внешней атмосферы космических аппаратов и станций
- •3.10.2. Особенности изменения давления в негерметичных отсеках геостационарных спутников
- •Глава 3.11. Загрязнение поверхностей космических аппаратов и методы его уменьшения
- •3.11.1. Источники загрязнения космических аппаратов
- •Глава 3.12. Аэрогазодинамика спускаемых аппаратов
- •3.13.2. Метеороиды
- •3.13.3. Космический мусор
- •3.13.4. Расчет вероятности непробоя КА метеороидами и техногенными частицами
- •3.13.5. Воздействия микрометеороидов и техногенных частиц на поверхность космического аппарата
- •3.14.2. Акустика и пульсации давления при старте ракет
- •3.14.3. Аэроакустические воздействия на ракеты в полете
- •3.14.4. Акустические воздействия на космические аппараты при наземной подготовке и в полете
- •4.2.1. Цели классификации
- •4.2.3. Систематическая классификация
- •Глава 4.3. Создание космических комплексов
- •4.3.2. Принципы обеспечения качества и надежности
- •4.3.3. Порядок создания космических комплексов
- •5.1.1. Теоретические основы проектирования летательных аппаратов
- •5.2.2. Схема многоуровневого исследования модернизации ракетного комплекса. Состав задач и математические модели
- •5.2.4. Задача оптимизации параметров модификаций ЛА. Математическая модель
- •5.2.6. Исследование эффективности модернизации РК
- •5.2.7. Анализ модификации ЛА с РДТТ при наличии неконтролируемых факторов
- •5.3.3. Проектирование топливных баков
- •5.3.4. Цилиндрические оболочки
- •Глава 5.5. Модели и методы исследования устойчивости и управляемости баллистических ракет
- •5.5.3. Исследование устойчивости продольных колебаний БР
- •Раздел 6. СРЕДСТВА ВЫВЕДЕНИЯ
- •Глава 6.1. Общая концепция
- •6.2.3 Ракеты носители «Циклон», «Зенит», «Зенит 3 SL»
- •6.3.3. МТКС «Спейс Шаттл»
- •Глава 6.4. Разгонные блоки
- •6.4.1. Разгонные блоки типа ДМ
- •6.4.2. Разгонные блоки типа «Бриз»
- •6.4.3. Разгонные блоки типа «Фрегат»
- •Глава 7.1. Жидкостные ракетные двигатели
- •7.1.1. Принципиальная схема ЖРД
- •7.1.3.1. Запуск
- •7.1.3.2. Работа ЖРД в полете
- •7.1.3.3. Автоматика ЖРД
- •7.1.3.4. Обеспечение устойчивой работы
- •7.1.4. Камера
- •7.1.4.1. Газодинамический расчет
- •7.1.4.2. Профилирование камеры
- •7.1.4.3. Тепловой расчет камеры
- •7.1.4.4. Конструирование камеры
- •7.1.4.5. Изготовление камеры
- •7.1.5. Газогенератор
- •Глава 7.2. Стендовые испытания двигательных установок
- •7.2.1. Задача отработки
- •7.2.2. Методика экспериментальной отработки жидкостных ракетных двигательных установок
- •7.2.4. Комплексные испытания пневмогидравлических систем и двигательных установок
- •Глава 8.1. Системы управления средств выведения
- •8.1.1. Назначение и область применения системы управления средств выведения
- •8.1.3. Функциональная структура и приборный состав систем управления средств выведения
- •8.1.4. Бортовой вычислительный комплекс и взаимодействие смежных систем
- •8.1.5. Навигация и наведение. Терминальное управление
- •8.1.6. Точность управления выведением полезного груза
- •8.1.7. Этапы развития систем управления средств выведения
- •8.1.9. Надежность и стойкость систем управления к помехам
- •8.1.10. Организация и обработка потоков информации о работе систем управления
- •8.1.11. Тенденция развития систем управления средств выведения
- •8.2.1. Бортовая аппаратура системы управления
- •8.2.2. Бортовое программное обеспечение
- •8.2.4. Наземная аппаратура системы управления
- •Глава 8.3. Системы разделения
- •8.3.1. Требования к системам разделения
- •8.3.2. Основные типы систем разделения
- •8.3.3. Исполнительные элементы систем разделения
- •8.3.4. Силы, действующие на разделяемые тела
- •8.3.5. Расчет систем разделения
- •8.3.6. Экспериментальная отработка систем разделения
- •8.3.7. Расчет надежности
- •8.5.1. Система одновременного опорожнения баков
- •8.5.2. Потребное давление наддува баков
- •Глава 8.6. Управление двигательной установкой
- •Глава 8.7. Исполнительные органы
- •Глава 8.8. Исполнительные приводы систем управления
Аджян А.П., Аким Э.Л., Алифанов О.М., Андреев А.Н. Ракетно-космическая техника. Машиностроение. Энциклопедия. T. IV-22 В двух книгах. Книга первая
СС ПЕРИОДИЧЕСКОГО ЗОНАЛЬНОГО ОБЗОРА НА КРУГОВЫХ ОРБИТАХ |
209 |
|
|
2.5.3.4. Некоторые закономерности оптимальных решений
Как отмечалось ранее, целевая функция за дачи периодического обзора, в отличие от задачи непрерывного обзора, существенно зависит от вращения Земли. По этой причине орбитальная структура оптимальной СС периодического обзо ра находится в сильной зависимости от высоты орбит спутников. Следствием этого является то, что анализ возможных орбитальных структур пе риодического обзора целесообразно проводить
для фиксированных протяженных диапазонов допустимого изменения высоты формирования СС. Для любого такого диапазона высот могут быть определены так называемые уровенные по4 верхности периодичности обзора — поверхности в
пространстве параметр |
«периодичность обзо |
ра – высота орбит |
полос обзора спут |
ников» при фиксированных значениях наклоне
ния орбит спутников |
4]. |
На рис. 2.5.14 |
показан фрагмент такой |
уровенной поверхности периодичности обзора
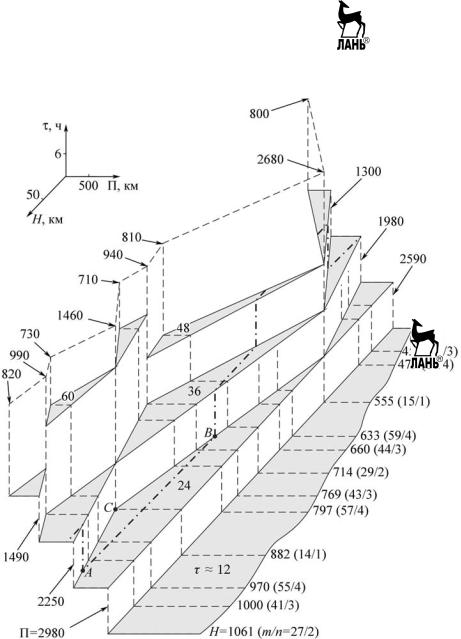
Рис. 2.5.14. Уровенная поверхность периодичности обзора для одиночного спутника в диапазоне высот 405…1061 км при наклонении i 85 и широтном поясе наблюдения 0…70

Аджян А.П., Аким Э.Л., Алифанов О.М., Андреев А.Н. Ракетно-космическая техника. Машиностроение. Энциклопедия. T. IV-22 В двух книгах. Книга первая
210 |
Глава 2.5. СПУТНИКОВЫЕ СИСТЕМЫ |
|
|
широтного пояса 0…70 для простейшей сис темы из одного спутника, движущегося по ор бите с наклонением i 85 . Для систем из большего числа спутников (двух и более) целе сообразно проводить анализ таких же уровен ных поверхностей периодичности обзора за данного района (вместо изучения отдельных частных вариантов оптимальных СС) при ус ловии оптимального выбора орбитальной структуры для каждой точки плоскости «высо та орбит – ширина полосы обзора спутников» в заданных условиях расчета уровенной по верхности (наклонение орбит, район наблюде ния и др.).
Действительно, из [5] известно, что оп тимальные (наименьшие) величины перио дичности обзора достигаются не для одного варианта орбитальной структуры, а для бес конечного подмножества орбитальных струк тур, характеризуемых такой оптимальной ве личиной периодичности. По этой причине решение классической задачи периодическо го обзора практически сводится к нахожде нию любого варианта орбитальной структу ры, характеризуемого оптимальным значени ем периодичности. Уровенные поверхности для многоспутниковых систем характеризуют достижимые значения наилучших (мини мальных) значений периодичности, каждое из которых может быть практически реализо вано на указанном подмножестве оптималь ных орбитальных структур.
В каждом своем сечении, задаваемом фиксированным значением высоты орбит в заданном диапазоне действительных чисел (или кратности т /п ГСО в соответствую щем диапазоне ограниченного множества рациональных чисел (см. п. 2.5.3), уровен ная поверхность имеет так называемую уро4 венную линию периодичности обзора — за висимость периодичности обзора, обеспе чиваемой СС с оптимальной орбитальной структурой, от ширины полос обзора спут ников системы. Можно показать, что в слу чае, когда орбитальная структура определя ется не оптимальным образом, получаю щиеся уровенные линии периодичности об зора для близких значений высот не «стыку ются» друг с другом. Следовательно, они не создают единой, физически понятной трех мерной поверхности «периодичность обзо ра — высота орбит — ширина полос обзора спутников». Данная ситуация имеет место, например, в случае построения уровенной
поверхности периодичности обзора, огра ничиваясь классом гарантированных СС (см. п. 2.5.3.1, 2.5.3.2).
На рис. 2.5.15 изображена уровенная поверхность для оптимальной двухспутни ковой СС (N 2). Данная уровенная по верхность рассчитана на основе оптимиза ции орбитальной структуры в классе регу
СС, содержащих для случая двух в системе (см. п. 2.5.3.2) абсо оптимальные орбитальные структу ры, характеризуемые наименьшими дости
жимыми значениями периодичности обзо ра. Из рис. 2.5.15 видно, что здесь уровен ные линии для различных значений высоты Н (кратностей т /п орбит) плавно переходят друг в друга и «укладываются» в уровенную поверхность, схожую с поверхностью для одиночного спутника.
Для трех и большего числа спутников в системе аналогичные уровенные поверхности могут быть получены расчетом оптимальной орбитальной структуры с использованием тео ретического подхода, изложенного в п. 2.5.3.3. Без принципиальных ограничений проведение расчетов столь же масштабных, как и в случа ях, представленных на рис. 2.5.14 и 2.5.15, здесь сопряжено с рядом трудностей техниче ского характера.
Базируясь на полномасштабных расчетах одно и двухспутникового оптимального обзо ра, а также на фрагментарных расчетах харак теристик оптимального обзора с помощью трех и более спутников в системе, можно ука зать ряд общих закономерностей локализации оптимальных решений задачи периодического обзора [1–5]. Рассмотрим эти закономерности на основе анализа уровенных поверхностей периодичности обзора для N спутниковой системы (N 6 1).
Из сравнения рис. 2.5.14 и рис. 2.5.15 видно, что уровенные поверхности для одно спутникового и двухспутникового оптималь ного обзора схожи по своему общему виду. Как показывают проведенные расчеты от дельных участков уровенных поверхностей для трех и большего числа спутников в сис теме, такая повторяемость в основных своих чертах свойственна уровенным поверхно стям периодичности обзора с помощью СС любого численного состава. Тот факт, что отдельные уровенные линии периодичности естественным образом укладываются на шкале высот, является косвенным призна
Аджян А.П., Аким Э.Л., Алифанов О.М., Андреев А.Н. Ракетно-космическая техника. Машиностроение. Энциклопедия. T. IV-22 В двух книгах. Книга первая
СС ПЕРИОДИЧЕСКОГО ЗОНАЛЬНОГО ОБЗОРА НА КРУГОВЫХ ОРБИТАХ |
211 |
|
|
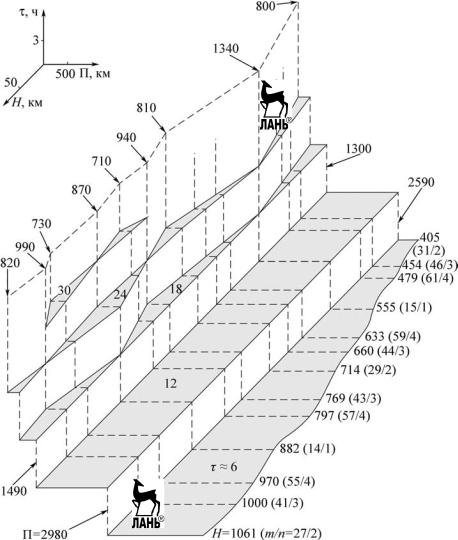
Рис. 2.5.15. Уровенная поверхность периодичности обзора для оптимальной двухспутниковой системы в диапазоне высот 405…1061 км при наклонении i 85 и широтном поясе наблюдения 0…70
ком правильности используемого математи |
дения (см. рис. 2.5.15) и в общем случае |
ческого аппарата поиска оптимальных вари |
1/2N части суток для N спутникового на |
антов СС. |
блюдения. |
Уровенная поверхность периодичности |
В направлении уменьшения периодично |
всегда имеет разрывный характер. При этом |
сти 9 (увеличения ширины П полос) уровен |
отдельные ее «куски» почти параллельны |
ная поверхность ограничена значениями П, |
плоскости «полоса–высота» и находятся на |
соответствующими нулевому (заданному ми |
уровнях некоторых периодичностей 9, при |
нимальному) углу места спутника относитель |
близительно кратных половине суток для од |
но плоскости местного горизонта объектов на |
носпутникового наблюдения (см. рис. 2.5.14), |
блюдения (находятся за пределами рис. 2.5.14, |
четверти суток для двухспутникового наблю |
2.5.15, справа от них). |

Аджян А.П., Аким Э.Л., Алифанов О.М., Андреев А.Н. Ракетно-космическая техника. Машиностроение. Энциклопедия. T. IV-22 В двух книгах. Книга первая
212 |
Глава 2.5. СПУТНИКОВЫЕ СИСТЕМЫ |
|
|
В направлении увеличения периодично сти 9 обзора (уменьшения П) в любом своем сечении, характеризуемом высотой ГСО за данной кратности
m / n const |
(2.5.55) |
(при отсутствии ограничений на число п), уровенная поверхность ограничена некото рым предельным значением величины 9, за висящим от периода повторяемости Tтр трас сы спутника на ГСО данной кратности m /n.
Однако в любом сколько нибудь продол жительном диапазоне высот уровенная по верхность в рассматриваемом направлении становится бесконечной. Это следует из воз можности сколь угодно большого повышения дискретности множества ГСО, имеющихся в фиксированном диапазоне высот, путем уве личения числа п эффективных суток в перио де повторяемости трасс спутников (см. п. 2.5.5.3). В пределе с увеличением п «нулевой» ширине П полосы соответствует периодич ность обзора 9 [ 1.
На рис. 2.5.14 уровенная поверхность представлена до величины 9 − 60 ч, на рис. 2.5.15 — 9 − 30 ч. Прерывистыми линиями на обоих рисунках показаны линии равных кратностей т /п, п 1…4.
Уменьшение периодичности 9 в любом сечении (2.5.55) с увеличением ширины
Пполосы происходит скачкообразно: функ ция 9(П) претерпевает разрывы первого рода (в целях повышения наглядности некоторые малые скачки периодичности на рис. 2.5.14,
2.5,15 сглажены, а соответствующие значе ния функции 9(П) приведены в усредненном виде).
Каждый «кусок» уровенной поверхности не строго параллелен плоскости «полоса–вы сота», а наклонен к ней под небольшими уг лами таким образом, что периодичность об зора возрастает с увеличением высоты Н при
Пconst и остается постоянной с изменени ем ширины П при H const. Такой наклон «кусков» уровенной поверхности объясняется тем, что различным точкам любого такого «куска» соответствуют однотипные по струк туре оптимальные последовательности сеан сов наблюдения (потоки наблюдений), кото
рые и определяют наибольший возможный перерыв в наблюдениях (т.е. периодичность 9 обзора). Числовое значение для этого макси мального перерыва зависит от драконическо
го периода Tдр обращения спутника таким об разом, что для двух различных высот H1, H2 с
драконическими периодами Tдр 1,Tдр 2 значе ния 91, 92 периодичности соотносятся в соот ветствии с выражением 91:92 Tдр 1:Tдр 2, что и предопределяет указанное изменение перио дичности для точек каждого «куска» уровен ной поверхности.
Каждой точке «куска» уровенной поверх ности при N 1 (см. рис. 2.5.14) соответствует строго определенный поток наблюдений кри тической точки наблюдаемого района, по скольку такой точке соответствует и единст венно определенная простейшая односпутни ковая орбитальная структура. Вместе с тем си туация при N 6 1 и, в частности, при N 2 (рис. 2.5.15) выглядит несколько иначе. Каж дой точке «куска» уровенной поверхности со ответствуют однотипные оптимальные потоки наблюдения критической точки, но соответст вовать ей в общем случае могут разные орби тальные структуры.
С точки зрения практики это нисколько не ухудшает ситуацию, поскольку чаще всего нас интересует любая из СС с лучшими ха рактеристиками. В противном случае имеем возможность оптимизации по дополнитель ным интересующим критериям на множестве указанных систем, являющихся оптимальны ми с точки зрения минимума периодичности обзора.
Важной особенностью уровенной поверх ности периодичности обзора для СС любого численного состава является качественная по вторяемость ее формы при изменении высоты
орбит спутников с |
соответствую |
щим перемене кратности |
/п как действи |
тельного числа на две |
например, из |
менению кратности суточной (п 1) орбиты с 14/1 14 на 16/1 16 или кратности двухсу точной (п 2) орбиты с 27/2 13,5 на 31/215,5. Последний указанный диапазон изме нения кратности т /п Ε [27/2, 31/2] показан на рис. 2.5.14, 2.5.15. Можно показать, что при соответствующей компенсации увеличения линейного размера ширины П полосы за счет изменения высоты Н можно обеспечить сов падение сечений каждой уровенной поверхно сти на границах указанного интервала. Это приводит к возможности унификации расче тов характеристик уровенных поверхностей для многоспутникового оптимального перио дического обзора и сведению данной задачи к изучению уровенных поверхностей только в

Аджян А.П., Аким Э.Л., Алифанов О.М., Андреев А.Н. Ракетно-космическая техника. Машиностроение. Энциклопедия. T. IV-22 В двух книгах. Книга первая
СС ПЕРИОДИЧЕСКОГО ЗОНАЛЬНОГО ОБЗОРА НА КРУГОВЫХ ОРБИТАХ |
213 |
|
|
указанных базовых интервалах изменения кратностей (высот) орбит.
Из анализа уровенных поверхностей пе риодичности обзора в указанном базовом ин тервале высот можно обнаружить следующую особенность локализации экстремумов функ ции 9(H,П) и П(H, 9). Такие экстремумы имеют тенденцию размещаться на уровенной поверх ности в районах высот Н, соответствующих геосинхронным орбитам с меньшими периода ми повторяемости трасс спутников (с мень шим числом п эффективных суток в этом пе риоде). Так, для односпутникового обзора (рис. 2.5.14) локальный минимум величины П при 9max − 24 ч соответствует ГСО кратности
т /п 14/1, при 9max − 36 ч т /п 41/3, 43/3, при 9max − 48 ч т /п 27/2, 29/2, 31/2, при 9max − 60 ч т /п 55/4, 57/4 и т.д.
Для оптимального двухспутникового об зора (рис. 2.5.15) аналогичные локальные экс тремумы располагаются чаще. Данным экстре мумам соответствуют следующие кратности: на
уровне 9max −18 ч т /п 43/3, 41/3, 9max − 24 ч т /п 14/1, 31/2, 29/2, 27/2, 9max − 30 ч т /п57/4, 55/4, 9max − 36 ч т /п 41/3, 43/3 и т.д.
Локальные минимумы периодичности 9 располагаются в районах тех же геосинхрон ных орбит, попадая в зависимости от реали зуемой максимальной ширины Пmax полосы на уровень того или иного значения 9.
Указанная особенность расположения экстремумов функций 9(H,П), П(H, 9) в рав ной степени относится как к интересующим нас минимумам, так и к максимумам этих функций. Действительно, например, для одно спутникового обзора (рис. 2.5.14) в районе геосинхронной орбиты кратности т /п 15/1 при любых 9max 6 24 ч могут иметь место толь ко максимумы ширины полосы. Более того, указанная особенность расположения локаль ных экстремумов рассматриваемых функций на уровенной поверхности не означает, что эти экстремумы «идут» строго в соответствии с возрастанием числа п эффективных суток в периоде повторяемости трассы. Имеется лишь общая тенденция в их размещении указанным выше образом. Например, кратностям т /п44/3, 59/4, 61/4, 46/3 с относительно малыми числами эффективных суток п для приведен ных на рис. 2.5.14, 2.5.15 случаев односпутни кового и оптимального двухспутникового об зора не соответствуют локальные экстремумы ни одной из указанных двух функций. Этим кратностям соответствуют экстремумы на уча
стках уровенных поверхностей, лежащих за пределами данных рисунков и относящихся к б льшим значениям периодичности 9. Проил люстрированная ранее на примере одно и двухспутникового оптимального обзора осо бенность локализации экстремумов функций 9(H,П) и П(H, 9) присуща уровенным поверх ностям для любого многоспутникового опти мального периодического обзора.
Изложенные особенности уровенных по верхностей имеют характер общих закономер ностей и могут быть успешно использованы при решении различных практических оптимизации высоты орбит и фазовой туры СС. Так, для решения классической
дачи периодического обзора (минимизации периодичности обзора при заданном значении ширины П Пmax полосы обзора) достаточно выявить точки линии пересечения уровенной поверхности с поверхностью П Пmax, имею щие наименьшую координату 9. Видно, что даже в случае односпутникового периодиче ского обзора решение такой задачи (по сути выбора только высоты орбиты спутника) име ет существенно не тривиальный характер.
Действительно, на рис. 2.5.14 в качестве примера штрих пунктиром показана линия пересечения указанных выше двух поверхно стей для Пmax 2 000 км. Наименьшую перио дичность 9 обзора имеют точки участка АВ этой линии (рис. 2.5.14). Соответствующий этому участку диапазон высот является наи лучшим с точки зрения осуществления одно спутникового обзора с минимальной перио дичностью для указанной ширины Пmax2 000 км полос обзора в рассматриваемых ус ловиях.
В случае решения другой практически важной задачи — минимизации потребной ширины полос обзора спутников при задан ном ограничении на периодичность 9 9max обзора анализ уровенных поверхностей перио дичности также оказывается весьма полезным. Для решения этой задачи оказывается доста точным найти точки уровенной поверхности, имеющие по возможности меньшую коорди нату П при условии их расположения не выше плоскости 9 9max . Например, в условиях рис. 2.5.14 для односпутникового обзора с ог раничением на периодичность 9 30 ч опти мальный вариант выбора высоты орбиты спут ника соответствует точке С.
Для решения различных практических за дач нет необходимости проводить трудоемкие

Аджян А.П., Аким Э.Л., Алифанов О.М., Андреев А.Н. Ракетно-космическая техника. Машиностроение. Энциклопедия. T. IV-22 В двух книгах. Книга первая
214 |
Глава 2.5. СПУТНИКОВЫЕ СИСТЕМЫ |
|
|
расчеты по подробному геометрическому по строению уровенных поверхностей, как это сделано на рис. 2.5.14 и 2.5.15. Для этого ока зывается достаточным ограничиться расчетом лишь относительно небольшого числа специ альных, так называемых опорных точек — зна чений целевой функции 9(H,П) в пространстве оптимизируемых параметров для заданных ис ходных данных. Исследования в этом направ лении с использованием теоретических поло
жений, изложенны |
п. 2.5.3.2, 2.5.3.3, позво |
ляют разработать |
различных практических |
приложений специальные процедуры оптими зации СС.
Смысл указанных опорных точек может быть в общих чертах пояснен с помощью сле дующего рассуждения. Из рис. 2.5.14 и 2.5.15 видно, что на краях отдельных «кусков» уро венных поверхностей, соответствующих раз личным фиксированным значениям перио дичности обзора, находятся точки пространст ва параметров «периодичность обзора – высо та орбит – ширина полос обзора спутников», характеризуемые минимально потребными для обзора с указанными периодичностями значе ниями ширины П полосы. В каждом сечении (2.5.55) уровенной поверхности координата П такой точки (9,П) — минимальная ширина полосы так называемого l4кратного покрытия заданного района, где под l кратным покры тием понимается такое покрытие, при кото ром в течение периода повторяемости трасс спутников системы каждая точка наблюдаемо го района не менее чем l раз попадает в зоны обзора этих спутников [1, 4, 6]. Указанные точки (9,П) обладают свойством оптимально сти по Парето, когда ни одну из характери стик 9 или П нельзя улучшить, не ухудшив другую. Переход от сечения (2.5.55) к полному пространству параметров 9,П, H сопровожда ется тем, что некоторые из указанных точек
(типа |
точки С в сечении т /п 14/1 на |
рис. 2 |
свойство оптимальности по Паре |
то |
храняют. |
Окончательное определение необходимо го используемых опорных точек зави сит от типа решаемой практической задачи и реализуемого алгоритма ее решения [3, 4].
Рассмотренные уровенные поверхности периодичности в пространстве параметров «периодичность обзора – высота орбит – ши рина полос обзора спутников» при фиксиро ванных значениях наклонения орбит спутни ков позволяют давать рекомендации по опти
мальному выбору высоты орбит формирова ния СС и ее фазовой структуры. Анализ пред почтительных значений наклонения i орбит может быть проведен с использованием анало гичных уровенных поверхностей периодично сти в пространстве параметров «периодич ность 9 — ширина П полос обзора спутни ков — наклонение i орбит» при фиксирован ной высоте Н (кратности т /п) геосинхронной орбиты.
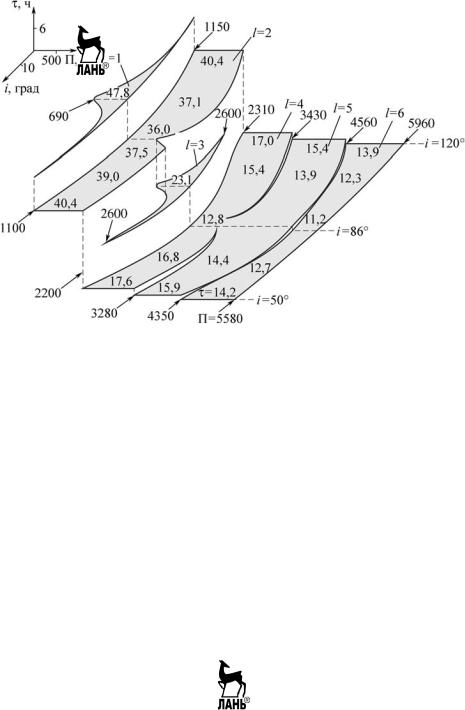
Рассмотрим пример такой уровенной поверхности для случая наблюдения широт ного пояса [0, i ], i min{i, i} одиночным спутником, движущимся по геосинхронной орбите заданной кратности т /n (рис. 2.5.16). Из рис. 2.5.16 видно, что данная уровенная поверхность образуется из «кусков», соответ ствующих различным кратностям покрытия l 1, 2, …, 6. Точки каждого такого «куска», расположенные на одной линии в направле нии изменения ширины П полосы обзора, характеризуются одинаковыми значениями периодичности в силу постоянства структуры потока наблюдений спутниками при фикси рованных наклонении i и кратности l покры тия. В направлении изменения наклонения значение периодичности обзора для точек та ких «кусков» меняется, что объясняется из менением структуры потока наблюдений (временн м сдвигом сеансов наблюдения в потоке) при сохранении постоянного числа l сеансов наблюдения в потоках. Различные получающиеся значения периодичности по казаны на рис. 2.5.16.
Из рис. 2.5.16 видно, что для нечетных кратностей l покрытия (l 1, 3, 5) соответст вующие им «куски» уровенной поверхности имеют впадины, приводящие к уменьшению потребной ширины полос обзора (для l 5 эта впадина не ярко выражена и приводит к незначительному уменьшению ширины по лосы, сглаженному при построении уровен ной поверхности на рис. 2.5.16). Такие ми нимумы ширины Пl max полос нечетного l кратного покрытия достигаются при на клонении i* arccos(n / m) для нечетной раз ности m n параметров т, п геосинхронной орбиты [1, 4]. Для рассматриваемого нечет ного случая m n 29 2 наклонение состав ляет i* 86 . Ярко выраженные минимумы потребной ширины полосы обзора прихо дятся на кратности покрытия l 1, 3 и соот ветствуют значениям периодичности 9 − 47,8; 23,1 ч (рис. 2.5.16).
Аджян А.П., Аким Э.Л., Алифанов О.М., Андреев А.Н. Ракетно-космическая техника. Машиностроение. Энциклопедия. T. IV-22 В двух книгах. Книга первая
СС ПЕРИОДИЧЕСКОГО ЗОНАЛЬНОГО ОБЗОРА НА КРУГОВЫХ ОРБИТАХ |
215 |
|
|
Рис. 2.5.16. Уровенная поверхность периодичности обзора широтного пояса [0, ji], ji min(i, p i) в пространстве параметров, включающем наклонение орбиты спутника, при m 29, n 2, N 1
Заметим также, что «куски» уровенной поверхности при четных кратностях l 2, 4, 6 имеют при наклонении i* 86 сильный «про гиб» в направлении изменения периодичности обзора. Это приводит к существенному выиг рышу в периодичности обзора за счет исполь зования наклонений, близких к указанному значению i* 86 в диапазонах изменения ши рины полосы обзора, соответствующих чет ным кратностям покрытия (рис. 2.5.16).
В практике баллистического проектиро вания СС периодического обзора нет необхо димости проводить геометрические построе ния уровенных поверхностей периодичности обзора, как это было сделано на рис. 2.5.14– 2.5.16. Более эффективным оказывается ком пьютерное построение цифровых моделей уро венных поверхностей периодичности на осно ве расчета опорных точек в пространстве пара метров «периодичность обзора — высота ор бит — ширина полос обзора спутников — на клонение орбит». Исследования в данном на правлении позволяют автоматизировать ряд этапов баллистического проектирования СС периодического обзора по заданным ограниче ниям, а также разработать различные практи ческие приложения.
СПИСОК ЛИТЕРАТУРЫ
1.Разумный Ю.Н. К оптимизации про ектно баллистических параметров спутнико вых систем периодического землеобзора // Ис след. Земли из космоса. 1993. № 1. С. 48–58.
2.Разумный Ю.Н. Маршрутная теория и результаты оптимизации спутниковых систем периодического обзора районов Земли (регу лярные и оптимальные системы) // Тр. II Меж дунар. конф. «Ракетно космическая техника: фундаментальные и прикладные проблемы», 18–21 ноября 2003 г., Москва. М.: Изд во МГТУ им. Н.Э. Баумана, 2005. Ч. 1. С. 118–137.
3.Razoumny Yu.N. Route Theory for Optimal Design of Satellite Constellations to Minimize Revisit Time in Low Earth Orbits // Proc. of the 56th Intern. Astronautical Congress, October 17–21, 2005, Fukuoka, Japan. IAC 05 C1.P.02. 11 p.
4, Razoumny Yu.N., Razoumny V.Yu.
Constellation Design for Earth Periodic Coverage in Low Orbits with Minimal Satellite Swath // Proc. of the 58th Intern. Astronautical Congress, September –28, 2007, Hyderabad, India. IAC 07 C 1.7.09.
19 p.
5. Разумный Ю.Н. Синтез орбитальных структур спутниковых систем периодического
