
- •3. Үзіліссіз функциялар. Кесіндідегі үзіліссіз функциялардың қасиеті.
- •5. Дифференциалданатын функциялардың негізгі қасиеттері. Бір айнымалы функция үшін Тейлор формуласы.
- •6. Функцияның интегралдануының қажетті және жеткілікті шарттары. Анықталған интегралдың орта мәні туралы теоремалар.
- •7. Бірінші және екінші текті меншіксіз интегралдар. Меншіксіз интегралдардың жинақтылығының жеткілікті шарттары.
- •10. Сандық қатарлар. Абсолют және шартты жинақты қатарлар. Қатар жинақтылығының жеткілікті шарттары.
- •11. Функционалдық тізбектер және қатарлар. Функционалдық тізбектер мен қатарлар бірқалыпты жинақтылығының жеткілікті белгілері.
- •13. Қос интегралдаудың негізгі қасиеттері. Қос интегралдауда және үш еселі интегралдауда айнымалыны ауыстыру.
- •14 Бірінші және екінші текті қисық сызықты интегралдар.
Математикалық талдау
Бірінші және екінші текті қисық сызықты интегралдар. 14
Бірінші және екінші текті меншіксіз интегралдар. Меншіксіз интегралдардың жинақтылығының жеткілікті шарттары. 7
Дәрежелік қатарлар және олардың жинақталу облысы.Дәрежелік қатарлар мүшелеп интегралдау және мушелеп диффференциалдау. Функцияларды дәрежелік қатарларға жіктеу. 12
Дифференциалданатын функциялардың негізгі қасиеттері. Бір айнымалы функция үшін Тейлор формуласы.5
Көп айнымалыдан тәуелді функция. Көп айнымалыдан тәуелді функцияның шегі. Көп айнымалыдан тәуелді функция үшін Тейлор формуласы. 8
Көп айнымалыдан тәуелді функцияның локалды экстремумы. Локалды экстремумның қажетті және жеткілікті шарттары. Шартты экстремум. 9
Қос интегралдаудың негізгі қасиеттері. Қос интегралдауда және үш еселі интегралдауда айнымалыны ауыстыру. 13
Сандық қатарлар. Абсолют және шартты жинақты қатарлар. Қатар жинақтылығының жеткілікті шарттары. 10
Тізбектер және оның шегі. Жинақты тізбектер және олардың қасиеттері.Тізбек жинақтылығының Коши критериі. 1
Үзіліссіз функциялар. Кесіндідегі үзіліссіз функциялардың қасиеті.3
Функционалдық тізбектер және қатарлар. Функционалдық тізбектер мен қатарлар бірқалыпты жинақтылығының жеткілікті белгілері. 11
Функция шегі.Функция шегінің бар болуының Коши критериі2
Функцияның интегралдануының қажетті және жеткілікті шарттары. Анықталған интегралдың орта мәні туралы теоремалар. 6
Функцияның үзіліс нүктелері және олардың классификациясы. 4
1.Тізбектер және оның шегі. Жинақты тізбектер және олардың қасиеттері.Тізбек жинақтылығының Коши критериі.
Натурал
сандар жиынында анықталған
 функциясының мәндерін сан тізбегі
немесе тізбек деп атайды.
функциясының мәндерін сан тізбегі
немесе тізбек деп атайды.
Егер тізбегіберілсе,
оны
тізбегіберілсе,
оны символыменбелгілейдінемесебылайжазады:
символыменбелгілейдінемесебылайжазады:
Анықтама
1.
Егеркезкелген үшін
үшін теңсіздігіорындалса,
онда
теңсіздігіорындалса,
онда тізбегінөспелідейді.
тізбегінөспелідейді.
Анықтама
2.
егеркезкелген үшін
үшін теңсіздігіорындалса,
онда
теңсіздігіорындалса,
онда тізбегінкемімелідейді.
тізбегінкемімелідейді.
Анықтама
3.
егеркезкелген үшін
үшін теңсіздігінқанағаттандыратындайоң
теңсіздігінқанағаттандыратындайоң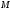 саны табылса, онда
саны табылса, онда тізбегіншектелгендепатайды.
тізбегіншектелгендепатайды.
Анықтама.Егерәрбіралдын
ала берілген санынасәйкес
санынасәйкес натурал саны
табылсажәнекезкелген
натурал саны
табылсажәнекезкелген нөмірлеріүшін
нөмірлеріүшін теңсіздігіорындалса,
онда
теңсіздігіорындалса,
онда санын
санын тізбегініңшегідепатайды.
Жазылуы:
тізбегініңшегідепатайды.
Жазылуы: немесе
немесе ұмтылғанда
ұмтылғанда депжазады.
депжазады.
Мысалы,
 тізбектіңшегін
табу керек.
тізбектіңшегін
табу керек.
Шешімі.
 болады.
болады.
Анықтама.Шегі бар тізбектіжинақтыдеп, шегіжоқтізбектіжинақсыздепатайды. Егертізбектіңшегі бар болса, ондатізбекшектелгенболады. Жинақтытізбектіңбірғанашегі бар. Жоғары (төменгі) жағынаншектелгенөспелі (кемімелі) тізбектіңшегі бар.
Анықтама. Егертізбектіңшегінөльгетеңболса, ондамұндайтізбектішексіз аз депатайды.
Теорема 1. Екішексіз аз тізбектердіңқосындысышексіз аз болады.
Теорема 2. Шектелгентізбектіңшексіз аз тізбеккекөбейтіндісішексіз аз тізбекболады.
Анықтама.
Егеркезкелген саны үшін
саны үшін нөмірітабылып,
барлық
нөмірітабылып,
барлық үшін
үшін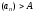 теңсіздігіорындалса,
онда
теңсіздігіорындалса,
онда тізбегіншексізүлкеншамадейдіжәнебылайжазады:
тізбегіншексізүлкеншамадейдіжәнебылайжазады: .
.
Теорема
3.
Егер тізбегі,
тізбегі,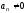 шексізүлкенболса,
онда
шексізүлкенболса,
онда тізбегішексізаз
жәнекерісінше
тізбегішексізаз
жәнекерісінше тізбегішексіз
аз болса, онда
тізбегішексіз
аз болса, онда тізбегішексіз
үлкен.
тізбегішексіз
үлкен.
Теорема
4. Егер және
және тізбектеріжинақтыболса,
онда
тізбектеріжинақтыболса,
онда
1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
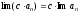 .
.
Егер ,
онда
,
онда
Жиіқолданылатыншектер
 –біріншітамашашек.
–біріншітамашашек.
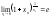 -екіншітамашашек.
-екіншітамашашек.
 тізбегіүшін
тізбегіүшін теңсіздігіорындалады.
Сондықтан
теңсіздігіорындалады.
Сондықтан жоғарыданшенелгенөспелітізбек.
жоғарыданшенелгенөспелітізбек.

шегі
бар болады.
 саныныңжуықмәні
саныныңжуықмәні болатыныдәлелденген.
Бұл сан Непер саны депаталады.
болатыныдәлелденген.
Бұл сан Непер саны депаталады.
2.Функция шегі.Функция шегінің бар болуының Коши критериі.
P
мен q
әріптерінің әрқайсысы c(c-нақты
сан) ,
c+0,c-0, ∞,+∞
және -∞
символдарының бірі, f
функциясы X
нақты сандар жиынында анықталып, p
сол
жиынның шектік нүктесі болсын. Егер
әрбір ε
оң саны үшін f
функциясының p-
ның белгілі бір ойылған δ(ε)-
маңайында қабылдайтын міндердің бәрі
де q-
дің маңайында жатса, онда x
p –
ға ұмтылғанда f(x)
функциясының шегі бар және q-
ға тең дейді де ,
 немесе
немесе символдармен белгіленеді.
символдармен белгіленеді.
Бұл жағдайды басқаша


 деп
те атайды.
деп
те атайды.
Дәлірек
p=a,
p=a+0, p=a-0
болғанда
 -ді
f функциясының a нүктесіндегі сәйкес
жай (екі жақты) , оң жақты және сол жақты
шегі деп, ал q=b,
q=b+0, q=b-0
болғанда f
функциясы
сәйкес b-ға,
b-ға
жоғарыдан,
b-ға
төменнен ұмтылады дейді.
-ді
f функциясының a нүктесіндегі сәйкес
жай (екі жақты) , оң жақты және сол жақты
шегі деп, ал q=b,
q=b+0, q=b-0
болғанда f
функциясы
сәйкес b-ға,
b-ға
жоғарыдан,
b-ға
төменнен ұмтылады дейді.
Шектің анықтамасы кванторлар тілінде былай жазылады:

Коши критерийі.
f
функциясы
X
жиынында
анықталып, a
нақты
саны сол жиынның шектік нүктесі болсын.
Онда f
функциясының
a
нүктесінде
нақты мәнді шегі бар болуы үшін, әрбір
ε оң саны бойынша X
жиынынан
алынған 0 және 0
және 0 теңсіздіктерін қанағаттандыратын кез
келгенx,y
сандары
үшін
теңсіздіктерін қанағаттандыратын кез
келгенx,y
сандары
үшін
 теңсіздігі орындалатындай δ оң саны
табылуы қажетті және жеткілікті.
теңсіздігі орындалатындай δ оң саны
табылуы қажетті және жеткілікті.
Кванторлар тілінде бұл теорема былай жазылады:
f-
тің а
нүктесінде нақты ( )(
)( )(
)( )
)
мәнді
шегі бар
: ε.
(1)
ε.
(1)
(1)- нің оң жағында жазылған шарт Коши шарты деп аталады.
Сонымен
Коши критерийін былай айтуға болады:
 функциясының
а нүктесінде
нақты мәнді шегі бар болуы үшін сол
нүктеде Коши шарты орындалуы қажетті
және жеткілікті.
функциясының
а нүктесінде
нақты мәнді шегі бар болуы үшін сол
нүктеде Коши шарты орындалуы қажетті
және жеткілікті.
3. Үзіліссіз функциялар. Кесіндідегі үзіліссіз функциялардың қасиеті.
Үзіліссіздіктің анықтамасы жөнінде жалпы ескертулер жасайық.
1 .Үзіліссіздіктің
анықтамасы келесі екі шарттың орындалуын
талап етеді: біріншіден, x x0-ге
ұмтылғанда f(x)-тің y0
нақты санына шегі бар, екіншіден y0
саны f функциясының x0
нүктесінде
қабылдайтын мәні болатын f(x0)
санына тең.
.Үзіліссіздіктің
анықтамасы келесі екі шарттың орындалуын
талап етеді: біріншіден, x x0-ге
ұмтылғанда f(x)-тің y0
нақты санына шегі бар, екіншіден y0
саны f функциясының x0
нүктесінде
қабылдайтын мәні болатын f(x0)
санына тең.
2 .Үзіліссіздік-локальді
ұғым.
.Үзіліссіздік-локальді
ұғым.
3 .
Жалпы жағдайда функцияның әрбір жеке
алынған нүктеге сәйкес мәнінің қалған
нүктелерде қабылдайтын мәндерімен
ешқандай байланысы жок. Мысалаы:
.
Жалпы жағдайда функцияның әрбір жеке
алынған нүктеге сәйкес мәнінің қалған
нүктелерде қабылдайтын мәндерімен
ешқандай байланысы жок. Мысалаы:
f(x)=
сәйкестігі
функция болады. Сонымен бірге ноль
нүктесінде мәні басқа мәндермен ешқандай
байланысы жоқ,себебі
 =f(0)
санына нақты болуынан өзге шарт
қойылмаған.
=f(0)
санына нақты болуынан өзге шарт
қойылмаған.
Ал
үзіліссіз функция үшін жағдай мүлде
басқа:
 нүктесінде f функциясы үзіліссіз
болса, онда f(а) саны f функциясының
а-ның «қасындағы» нүктелерде қабылдайтын
мәндері арқылы табылады. Дәл айтқанда
f(а) саны
нүктесінде f функциясы үзіліссіз
болса, онда f(а) саны f функциясының
а-ның «қасындағы» нүктелерде қабылдайтын
мәндері арқылы табылады. Дәл айтқанда
f(а) саны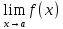 шегіне тең, ал сол шектің анықтамасында
f функциясының а нүктесінде қабылданатын
мәні қатыспайды,тіпті бар болуы да
қажетті емес.
шегіне тең, ал сол шектің анықтамасында
f функциясының а нүктесінде қабылданатын
мәні қатыспайды,тіпті бар болуы да
қажетті емес.
4 .
. болғандықтан
үзіліссіздіктің анықтамасындағы 1-
теңдікті былай да
болғандықтан
үзіліссіздіктің анықтамасындағы 1-
теңдікті былай да жазуға болады.
жазуға болады.
5 Үзіліссіздіктің x→
Үзіліссіздіктің x→ f(x)
→
f(x)
→ түріндегі анықтамасын үзіліссіздіктің
x→
түріндегі анықтамасын үзіліссіздіктің
x→ символының екі жағын да
символының екі жағын да ережесін қолданғанда , сондағы ұмтылу
сақталатынын белгілейді деп түсінуге
болатынын көрсетеді.
ережесін қолданғанда , сондағы ұмтылу
сақталатынын белгілейді деп түсінуге
болатынын көрсетеді.
Үзіліссіз функциялар шарттарды қанағаттандырады,сондықтан аталған теоремалардан салдар ретінде үзіліссіз функциялардың келесі маңызды қасиеттері шығады:
1-теорема. Әрбір функцияның үзіліссіздік нүктесі локальді шенелу нүктесі болды.
2-теорема.
Егер f функциясы
 үзіліссіз
болып, сол нүктеде қабылданған
үзіліссіз
болып, сол нүктеде қабылданған ) мәні оң (теріс) болса, онда
) мәні оң (теріс) болса, онда белгілі бір маңайында
белгілі бір маңайында мәндері де оң (теріс) болады.
мәндері де оң (теріс) болады.
Салдар.
Егер
 функциясы
функциясы үзіліссіз болып,оның белгілі бір ойылған
маңайындағы барлық нүктелерде қабылданатын
мәні нольге тең болса не
үзіліссіз болып,оның белгілі бір ойылған
маңайындағы барлық нүктелерде қабылданатын
мәні нольге тең болса не -дің
кез келген ойылған маңайында оң және
теріс таңбалы мәндерді қатар қабылдаса,
онда
-дің
кез келген ойылған маңайында оң және
теріс таңбалы мәндерді қатар қабылдаса,
онда )=0 болады.
)=0 болады.
4.Функцияның үзіліс нүктелері және олардың классификациясы.
Егер
 нүктесі
f функциясының анықталу жиынында жатып,
f сол нүктеде үзіліссіз болмаса,
нүктесі
f функциясының анықталу жиынында жатып,
f сол нүктеде үзіліссіз болмаса, онда
нүктесі f-тіңүзіліс
нүктесі
немесе нүктесінде үзіледі
дейді. Үзіліссіздік жағдайындағыдай,
үзіліс нүктесінің (үзілістіктің) әртүрлі
өзара эквивалентті анықтамалары бар.
онда
нүктесі f-тіңүзіліс
нүктесі
немесе нүктесінде үзіледі
дейді. Үзіліссіздік жағдайындағыдай,
үзіліс нүктесінің (үзілістіктің) әртүрлі
өзара эквивалентті анықтамалары бар.
Егер
белгілі бір
 оң
саны мен кез келген
оң
саны мен кез келген оң
саны үшін
оң
саны үшін
 теңсіздіктері
орындалатын
теңсіздіктері
орындалатын
 саны
табылса өрнегі жазылғандықтан, алдын
ала
саны
табылса өрнегі жазылғандықтан, алдын
ала саны
f-тің анықталу жиынында жатады деп
ұйғарамыз, немесе егер белгілі оң саны
үшін
саны
f-тің анықталу жиынында жатады деп
ұйғарамыз, немесе егер белгілі оң саны
үшін шарттарын
қанағаттандыратын
шарттарын
қанағаттандыратын тізбегі
бар болса, онда f функциясы
тізбегі
бар болса, онда f функциясы нүктесінде
үзіледінемесе
нүктесінде
үзіледінемесе үзіліс
нүктесі дейді.
үзіліс
нүктесі дейді.
Егер
f функциясы
 нүктесінде
үзілісті болып, сол нүктеде оның сол
және оң жақты нақты мәнді шектері бар
болса, онда f функциясы
нүктесінде
үзілісті болып, сол нүктеде оның сол
және оң жақты нақты мәнді шектері бар
болса, онда f функциясы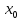 нүктесінде
жай немесебірінші
түрдегі үзілісті дейді.
Бірінші түрдегі үзіліс тек мына төрт
жағдайдың бірінде ғана мүмкін:
нүктесінде
жай немесебірінші
түрдегі үзілісті дейді.
Бірінші түрдегі үзіліс тек мына төрт
жағдайдың бірінде ғана мүмкін:
f( )=f
(
)=f
( )
)
f( )=f
(
)=f
( )
) ,
,
f( )
)
f( 0)
0)
Егер
f функциясы
 нүктесінде
үзілісті болып, бірақ үзіліс бірінші
түрдегі үзіліс болмаса, дәл айтқанда,
нүктесінде
үзілісті болып, бірақ үзіліс бірінші
түрдегі үзіліс болмаса, дәл айтқанда, нүктесінде
f-тің кемінде бір біржақты нақты мәнді
шегі болмаса, онда f функциясы
нүктесінде
f-тің кемінде бір біржақты нақты мәнді
шегі болмаса, онда f функциясы нүктесінде
күрделі немесеекінші
түрдегі үзілісті
дейді.
нүктесінде
күрделі немесеекінші
түрдегі үзілісті
дейді.
 cаны
f функциясының
cаны
f функциясының нүктесіндегісекірмесі
деп аталады, өзара тең оң және сол жақты
нақты шектері бар болғанда, яғни секірме
ноль болатын, жағдайдың бір ерекшелігі
бар: f функциясын бір ғана
нүктесіндегісекірмесі
деп аталады, өзара тең оң және сол жақты
нақты шектері бар болғанда, яғни секірме
ноль болатын, жағдайдың бір ерекшелігі
бар: f функциясын бір ғана
 нүктесінде
өзгертіп, сол нүктеде үзіліссіз
болатынфункцияға айналдыруға
болады
нүктесінде
өзгертіп, сол нүктеде үзіліссіз
болатынфункцияға айналдыруға
болады =f(x),eгер
=f(x),eгер болса,
болса, =f
(
=f
( ),
x=
),
x= егер
болса
егер
болса
сондықтан, кейде секірмесі нольге тең болатын үзілісті жөнделетін үзіліс деп атайды.
