Материальный баланс процесса Фишера-Тропша

Приход		Расход
Gj,0	кг/ч	Gj	Кг/ч
	26,7 186,8		9,6 14,5 19,8 5,9 5,1 5,9 69,4 74,8 8,5
Сумма	213,5	Сумма	213,5

Интегральный тепловой баланс химического реактора

Его можно записать, например, так (кДж/время):

Q₁+ Q₂+ Q₃+ Q₄= Q₅+ Q₆+ Q₇, где

Q₁, Q₅– тепло, вносимое в аппарат и выносимое из него со всеми физическими потоками;

Q₂– тепло, подводимое (отводимое) к аппарату через поверхность теплопередачи;

Q₃— суммарное тепло всех химических реакций;

Q₄— суммарное тепло всех физических процессов;

Q₆— теплопотери в окружающую среду;

Q₇— тепло, расходуемое на нагревание материала аппарата (учитывается для нестационарного режима работы аппарата, например, для периодических процессов).

Теперь можно записать: Q₂= Q₅+ Q₆+ Q₇— Q₁— Q₃— Q₄.

Если Q₂положительно, то тепло подводят к аппарату и, если отрицательно, то отводят. Для адиабатического режима Q₂=0.

Найденная величина Q₂позволяет определить:

Кинетика:

1. где S_T— поверхность теплопередачи; К_Т— коэффициент теплопередачи, учитывающий все механизмы передачи тепла;.

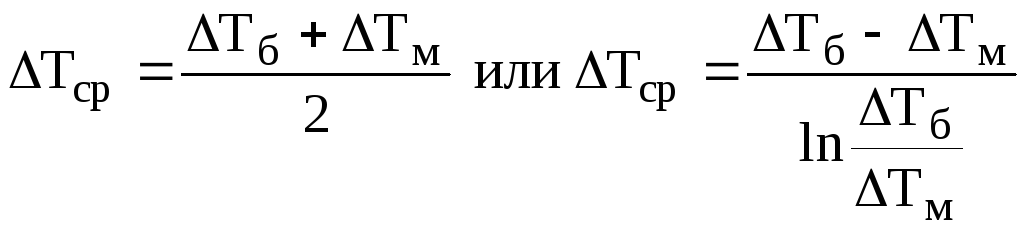— средняя движущая сила теплопередачи;

Статика:

2) где G_T— массовый расход теплоносителя (хладагента);– массовая теплоемкость теплоносителя;

Т_Т=Т_То–Т_Тк– разность температур теплоносителя от входа в аппарат до его выхода.

Если расход G_Tбыл выбран, то определяют Т_Тк.

Если нагревание (охлаждение) реакционной смеси идет за счет фазового перехода теплоносителя, то где– массовая удельная теплота фазового перехода теплоносителя (например, конденсации или испарения).

Запишем реакцию

где H=_Bh_B+_Zh_Z–_Ah_A–_Yh_Y, гдеh_j–удельная мольная энтальпия веществаj[кДж/мольj].– Мольный тепловой эффект этой реакции (кДж/моль).

– мольный тепловой эффектi-й стадии;

j– вещества, участвующие наi-той стадии.

– суммарный тепловой эффект всех р стадий.

Связь между и тепловыми эффектами превращения 1 кмоль j-го вещества_j(кДж/кмоль j) или 1 кг этого вещества(кДж/кг j) следующая:

где_jвсегда берется со знаком (+).

Пример.

Имеется реакция 2A+ 3Y4B+Z+H.

H= 80 кДж/моль. НайтиH_A,H_B,H_Y,H_Z.

Решение.

H_A= 80/2 = 40 кДж/мольА,H_Y= 80/3 = 26,7 кДж/мольY,

H_B = 80/4 = 20 кДж/мольB и H_Z = 80/1 = 80 кДж/мольZ.

Тепловые эффекты химических реакций зависят от температуры по закону Кирхгофа:

(j — продукты, j,0 — реагенты)

Часто с_рмало и в этом случае в технических расчетах поправок на температурную зависимостьН не делают (или при этом интервал Т₀– Т невелик).

Выберем теперь некоторый температурный уровень Т_осн, от которого будем вести тепловые расчеты.

Теперь — температура потока на входе в аппарат, К.

Если на температурном интервале Т_оснТ₀можно считать=const (или, приняв для расчета

, то

Если принять Т_ОСН=273 К, то

где t₀— температура потока на входе в реактор,^оС;n– число веществ на входе в реактор.

То же самое можно записать для Q₅:

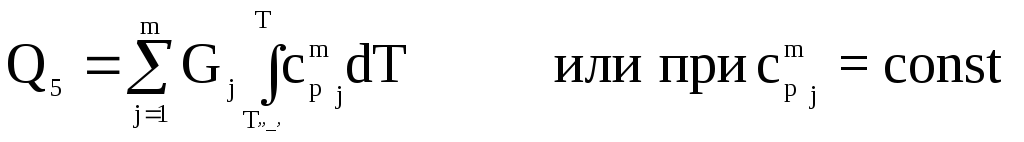(гдеm– число веществ на выходе из реактора) на интервале Т_ОСНТ имеем:

Если Т_ОСН=273 К, то

где Т и t — температура потока на выходе из аппарата, соответственно К и^оС.

Найдем теперь гдеG_j= G_j—G_j,0— для продуктов,

G_j= G_j,0—G_j— для реагентов.

р — число химических реакций (стадий).

(–) — берется из справочников или рассчитывается, например при Т_ОСН=273 или 298 К.

Для физических процессов имеем где q_j^m— удельный тепловой эффект физического превращения вещества j, определенный при температуреtв реакторе. Чаще всего это фазовый переход.

Следует обратить внимание на то, что экзотермический эффект по термодинамической шкале обозначается (—Н), а по термохимической +q.

Величину Q₇находят так:

Q₇=, то

где m_ап— масса аппарата;— массовая теплоемкость материала аппарата; t₀и t — начальная и конечная температуры аппарата.

Тепловые потери Q₆ вычисляют по известным методикам:

1. по допустимой температуре на внешней стенке аппарата (требование санитарных норм и ТБ);

2. по допустимой доле тепловых потерь, например, от суммарного теплового эффекта процесса, т.е. от Q₃+Q₄или от Q₃.

Если требования пунктов 1-2 не выполняются, то ставят теплоизоляцию.

Все Q₁Q₇должны иметь одну и ту же размерность.

Для периодических процессов тепловой баланс составляется на самый теплонапряженный момент времени. Если в периодическом реакторе есть нагрев и затем охлаждение (или наоборот), то расчеты ведутся на оба периода отдельно. Отдельно определяют расход теплоносителя и хладагента.

Теплопотери рассчитывают на зимний период. Если аппарат охлаждают окружающим воздухом, например в градирне, то расчеты ведут на летний период.

Часто в зоне теплоносителя тепло выделяется за счет химической реакции, например, горения топлива. Тогда для определения расхода топлива (и воздуха) нужно составить тепловой баланс для этой зоны:

где

G_T,0, G_B,0, G_д— массовые расходы топлива, воздуха и дымовых газов;

— массовые теплоемкости топлива, воздуха и дымовых газов;

t_T,o, t_B,o, t_д — температура топлива и воздуха на входе в зону горения и дымовых газов на выходе их нее;

– тепловой эффект реакции горения топлива (низшая теплотворная способность топлива).

Если воздух и топливо не подогреваются в регенераторах (рекуператорах), то (в технических расчетах принимают равными 0).

Зная химизм процесса горения и коэффициент избытка воздуха, можно массовые расходы воздуха и дымовых газов выразить через массовый расход G_T,0. Например, G_В,0= G_T,0К_Ви G_д= G_T,0К_д, где К_Ви К_д– соответствующие коэффициенты пропорциональности, получаемые из стехиометрии процессов горения.

Тогда (без подогрева воздуха и топлива): и при подогреве воздуха

Пример.

Найти поверхность теплопередачи в реакторе синтеза Фишера-Тропша, используя данные предыдущего примера. Известно, что t₀= 206^оС,t= 210^оС. Выделяющееся тепло реакции отводится кипящим конденсатом с температуройt_Т= 200^оС. Тепловой эффект образования метанакДж/кгСН₄, а остальных углеводородов и спиртов можно принять равнымкДж/кгRH. Средняя массовая теплоемкость [кДж/(кг^оС)] равна для СО – 1,1, Н₂– 14,5, Н₂О – 2,3, СН₄– 2,8,RH– 1,8. В качестве температуры основного уровня выбрано 25^оС. Коэффициент теплоперерачи может меняться от 460 до 510 вт/м²^оС.

Режим – стационарный, теплопотерями пренебречь.

Решение.

В нашем случае

Тепло нужно отводить.

Определим движущую силу теплопередачи ^оС, гдеt_биt_ь– большая и меньшая разности температур теплоносителя и реакционной массы.

Рассчитаем необходимую поверхность теплопередачи для наихудшего варианта, когда К_Т= 460 вт/м²^оС = 0,46 квт/м²^оС. Тогда имеем:

(м²).

Определение основных размеров аппарата

1. периодического действия.

Используя данные материального баланса, переходят от массового количества перерабатываемых материалов к объемному:

где G₀— общая масса перерабатываемых материалов;

₀— их средняя плотность.

Эти соотношения справедливы для жидких и сыпучих материалов. Газы в периодических условиях практически не перерабатываются.

Полный цикл работы аппарата периодического действия равен (кинетическая характеристика периодического процесса):

где_i— продолжительность одной i-ой операции: f — число операций в цикле.

Можно также записать _ц=+_нз, где— время переработки сырья в продукты,_нз— время непроизводительных затрат. Если>_нз, то можно (рационально) организовывать периодический процесс. Все_iопределяются экспериментально путем хронометража.

Выбирают некоторый (в первую очередь стандартный) аппарат с известным полным объемом V_п. Теперь число параллельно работающих аппаратов равно:

где V= V_п. Здесь— это коэффициент заполнения аппарата, который всегда меньше единицы.

Для примера можно рассмотреть выбор батареи коксования. Задано, например, количество доменного кокса, которое должна вырабатывать батарея (это G_B). Учитывая количество (выход) доменного кокса от общего (валового) кокса, рассчитывают количество валового кокса. Для кокса, т.к.Х_А=1 (вся шихта должна превратиться в углеродистый остаток), т.е. выход равен селективности. Зная выход валового кокса из используемой в данном производстве шихты, находят количество (массу) шихты. Зная насыпную массу шихты, находят объем перерабатываемой шихты (т.е. W₀) в единицу времени,

Выбирают камеру коксования с V_п. Зная_цкамеры коксования, определяют n — число камер в батарее:

где V_кокса= V_п. Здесь– это коэффициент заполнения камеры коксования шихтой.

2. Непрерывного действия

Для жидкофазных потоков и потоков сыпучих материалов объемный поток перерабатываемых материалов определяют так же, как и в периодических процессах с использованием G_j,0и_j,0.

Для газовых потоков используют для расчетов уравнение состояния реальных газов: где Z_j,0— коэффициент сжимаемости j-го компонента потока на входе в реактор (Z_j,0рассчитывается с использованием приведенных температуры и давления вещества j, т.е.и;.

р₀, Т₀— давление и температура потока на входе в реактор. Считают, что выполнимо

Объем аппарата рассчитывают, используя такие кинетическиехарактеристики процесса, как время контакта, объемную скоростьu, удельную производительностьg.

Если W=W₀=const, то[u] - [время^-1].

Если WW₀, тоЗдесь₀—условноевремя контакта, определяемоедля условий системы на входев аппарат.

Если удельная производительность аппарата задана по целевому продукту В, то где G_B— массовая производительность по целевому продукту (кг В/с);

g_В— удельная массовая производительность по целевому продукту [кг В/(м³с)]. Для каталитических процессов размерность удельной производительности по целевому продукту такова: кг В/(кг_катс).

Тогда Зная, например, насыпную массу зернистого катализатора, находят его объем:где_кат— насыпная плотность слоя катализатора.

Нахождение сечения аппарата и его высоты (длины) возможно при использовании в расчетах такой экспериментальной величины как линейная скорость потока w.Если объем системы меняется, т.е. WW₀, то используют в расчетах линейную скорость w₀на входе в аппарат. Тогдагде S — полное сечение аппарата.

Если аппарат имеет насадку, то полное сечение (включая насадку) будет равно: — фиктивная линейная скорость (т.е. отнесенная к общему сечению аппарата).

Истинная линейная скорость (отнесенная к свободному, не заполненному насадкой сечению аппарата) определяется так: — доля свободного сечения аппарата (<1 иw₀>w₀*), (- это порозность слоя).

Рабочая высота пустотелого аппарата (без насадки) равна: илиL=w₀*₀(аппарат с насадкой).

Полная высота равна где— коэффициент заполнения аппарата (1).

Для контактно-каталитических процессов имеем:

L_п=L+L*, L* — суммарная высота встроенных теплообменников, газораспределительных устройств и др.

Число параллельно работающих аппаратов определяется так: где S_c— сечение аппарата, взятого из каталога (стандартного).

Пример.

Найти основные технологические размеры реактора Фишера-Тропша. Для расчета использовать экспериментально найденные значения = 1 м/с,₀ = 9 с иg₀= 0,1111нм³/м³с, а такжеF₀= 20 кмоль/ч илиW₀= 2022,4/3600 = 0,1244 нм³/с. Диаметр трубки реактораd, в которую загружается катализатор, принять равным 0,032 м.

Решение.

Найдем рабочий объем м³или

(м³).

Общее сечение трубок с катализатором:

(м²).

Число трубок в реакторе:

штук.

Рассчитаем высоту трубок.

(м).

Определим поверхность теплопередачи:

(м²).

Этой поверхности хватит, чтобы отвести из реакционного объема выделяющееся тепло реакции.

Расчет аппаратов по математическим моделям

Уравнения нестационарного массо- и теплопереноса с источниками

Выделим произвольный объем V, отделенный от остального пространства произвольной поверхностью S. За малый промежуток времени учтем изменение количества вещества j в объеме V за счет всех физических потоков, пересекающих поверхность S, и химических реакций внутри V, т.е. за счет источников. Условия в V неоднородны, поэтому разбиваем V на бесконечно малые (изотропные) объемы и проводим интегрирование по всему объему. Тогда за счет химических реакций, в которых участвует j, за времяво всем объемеVпроизойдет изменение его количества:где_ijположительно, если на этой стадии j образуется, и отрицательно, если расходуется.

dV=dxdydz(берется интеграл по объему или тройной интеграл поx,y,z).

Физические потоки — это конвекцияиперенос веществаза счет любого механизма, аналогичногозакону Фика(диффузия) (перенос за счет градиента концентрации).

Разобьем всю поверхность S на бесконечно маленькие участки.

Если такой участок расположен не перпендикулярно градиенту концентрации j, то удельный диффузионный поток (–D_j)gradC_j(где D_j– коэффициент диффузии вещества j) нужно разложить на две составляющие: нормальную (–D_jgradC_j)_nи тангенциальную. За счет первой составляющей вещество j переносится через поверхность реакционного пространства, а за счет тангенциальной составляющей будет скользить вдоль границы поверхности, не пересекая ее. За времяза счет диффузии через всю поверхность S будет перенесено вещества j столько:(поверхностный или двойной интеграл).

, где С – скалярная величина.

Конвективный поток также разобьем на нормальную и тангенциальную составляющие. За время за счет нормальной составляющей конвективного потока через поверхность S будет перенесено вещества j столько:где w_n— линейная скорость нормальной составляющей конвективного потока,C_j– концентрация веществаjв выделенном элементарном объемеdV(или на выходе из него).

В нестационарном процессе будет происходить накопление (со знаком плюс или минус) вещества j в объеме V. За время в некоторой точке f объема V концентрация j будет меняться от C_j(,f) до C_j(+,f). Тогда накопление вещества j в объеме V составит:

Можно записать: (здесь осуществлен предельный переход). Поберется частная производная, т.к. возможны изменения концентрации вещества j и в пространстве (например, берутся координаты не f, а другой точки).

Теперь можно записать (деля и умножая тройной интеграл на и устремляя :0):

Запишем материальный баланс по веществу j (приход j—расход j=накопление j):

Умножим все на (-1) и проведем некоторые преобразования:

Для дальнейших преобразований используем формулу Остроградского-Гаусса:

(Сумма первых частных производных по координатам х, у,zот векторной величины).

Теперь запишем:

Здесь w– векторная величина.

Известно, что если то и=0, где— некоторая функция.

Тогда имеем:

или

Это уравнение нестационарного массопереноса с источниками.

Следует записать: div(C_jw)=wgradC_j+C_jdivw.

Если w=const, т.е. C_jdivw=0, то:

Если при этом и D_j=const, то

Известно, что:где– это оператор Лапласа,(набла) – оператор Гамильтона.

Если используется тело объемом V с цилиндрической симметрией (l, R — переменные длина и радиус цилиндра), то можно записать:

Тепловой баланс (или баланс энтальпий, т.к. рассматривается аппарат, в котором давление постоянно) составим для V за . Запишем изменение энтальпии в объеме V за:

где h_j– удельная мольная энтальпия вещества j, (кДж/кмольj); C_jh_j– энтальпия единицы объема реакционной смеси (кДж/кмольjкмольj/м³ кДж/м³), j – любое вещество, включая инертный растворитель. C_jh_j– связано с источником, т.к. С_j зависит от скоростиr_i.:

Изменение энтальпии (уравнение Фурье) происходит за счет наличия конвективного переноса вещества j и теплопроводности реакционной смеси. Изменением энтальпии за счет термодиффузии, которая намного меньше теплопроводности, пренебрегаем. Тогда можно записать:

где — коэффициент теплопроводности; Т — температура потока, пересекающего элемент поверхности dS.

Тепловой баланс (приход—уход=накопление) выглядит так (проведено сокращение на ):

Используя теорему Остроградского-Гаусса, получим (после переноса слагаемых вправо):

и далее так:

Запишем некоторые преобразования:

, гдеh_j=f(T).

Кроме того:

,h_j– скаляр.

Из уравнения материального баланса, пренебрегая переносом тепла за счет диффузии, имеем:

Тогда (после сокращения ):

Сумма не зависит от порядка слагаемых, поэтому:

— это изменение энтальпии веществ в i-ой реакции, т.е. это тепловой эффект i-ой реакции_i(см. стр.20).

Кроме того заметим, что

Теперь имеем:

Решить полученные дифференциальные уравнения материального и теплового балансов можно, зная граничные условия. Граничные условия — это то, что известно нам на границе системы: концентрации веществ, температуры, мольные потоки веществ, тепловые потоки и др.

Когда условия в Vанизотропные, то уравнение, отвечающее за теплопередачу в энтальпийном балансе, записывается как граничное условие. Если изотропны, то как слагаемое теплового баланса.

Реактор периодического действия

Для переработки жидкостей — это аппараты с мешалкой. При использовании быстроходных мешалок (турбинные, пропеллерные) аппараты снабжаются отражательными перегородками. Можно организовать процесс, осуществляя циркуляцию реакционной массы через выносной теплообменник. Его поверхность не лимитируется размерами аппарата. Для гомогенных систем интенсивное перемешивание ликвидирует застойные зоны и увеличивает коэффициент теплоотдачи от реакционной массы к поверхности теплопередачи. Аппарат периодического действия предполагает, что за время осуществления процесса в рабочий объем не вводят и из него не выводят материальные потоки. Математическая модель реактора периодического действия позволяет определитьдаже для неизотермических условий при различных начальных условиях.

В периодических условиях практически всегда перерабатывают системы с неменяющимся (постоянным) объемом.

Для реактора периодического действия div(wC_j)=0 иdiv(D_jgradC_j)=0. Изменение С_jпроисходит только во времени, оставаясь одним и тем же в любой точке объема аппарата. Поэтому в уравнении матбаланса используют знакd, а не. Тогда:Здесь_ijберется со знаком минус для расходующихся веществ и со знаком плюс для образующихся на i-ой стадии процесса. Например, для:

Для простой реакции (одностадийной) удобно использовать степень превращения Х_А. Например, дляможно записать:

Так, для реакции первого порядка имеем:

Для неизотермических условий нужно знать изменение Т во времени, что позволяет рассчитывать k_Ав любой момент времени. Это достигается путем составления теплового баланса для периодического реактора, которое выглядит так:

– общий вид.

Для периодического реактора:

Теперь

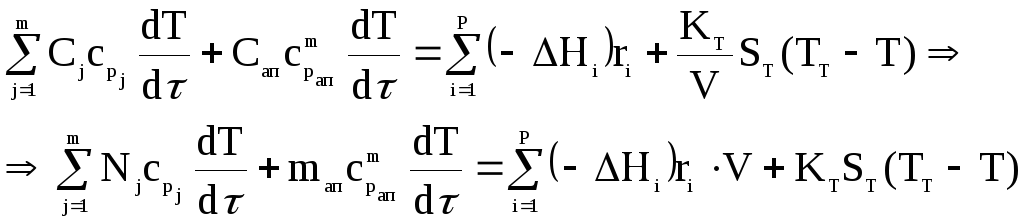-удельная поверхность теплопередачи

Для простой реакции :

где .

Если Т_Tconst, то находят связь между Т и Т_Тиз теплового баланса по теплоносителю:Выбирают G_Tи, зная Т_Т⁰, находят Т_Т=f(Т).

Адиабатический режим

Это означает, что

Для простой реакции при адиабатическом режиме имеем:

Если считать, что c_pj=const иc_pi0, то после интегрирования (от 0 до Х_Аи от Т₀до Т) получим:

Очевидно, что