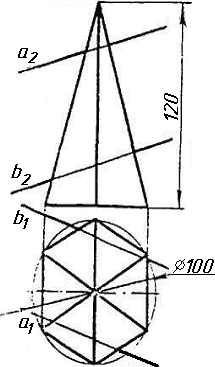
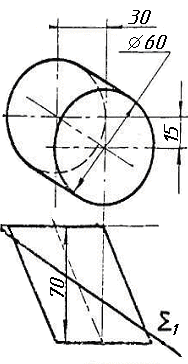
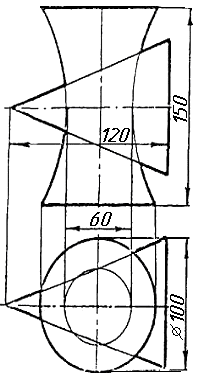
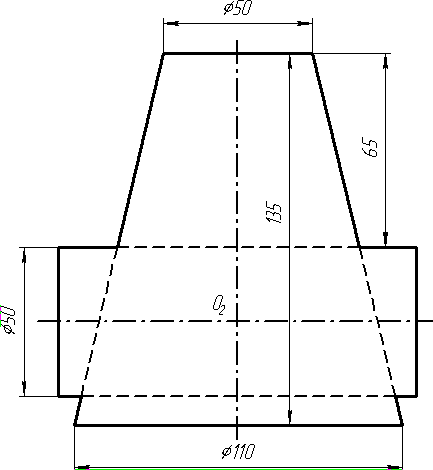
Контрольні питання

• Які лінії утворюються при перетині многогранників?

• Який план рішення задачі на перетин поверхонь?

• Як вибирають площину посередник?

• Які умови необхідні для рішення задач способом сферичних посередників?

• Сформулюйте план рішення задач за допомогою сферичних посередників.

• Як визначається видимість точок лінії перетину поверхонь?

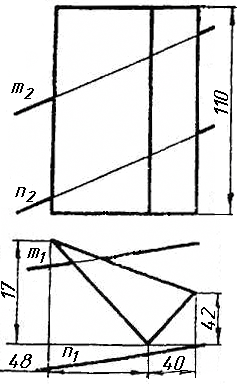
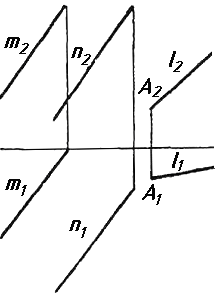
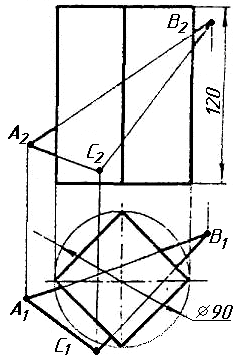
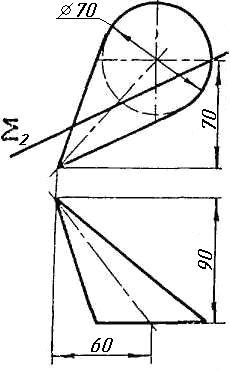
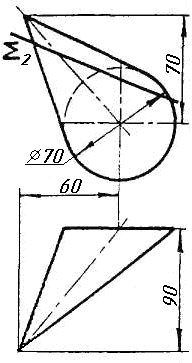
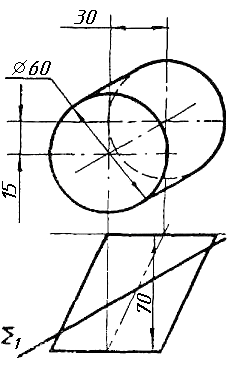
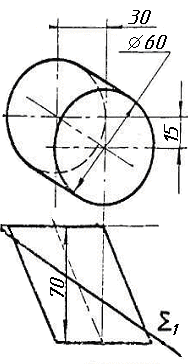
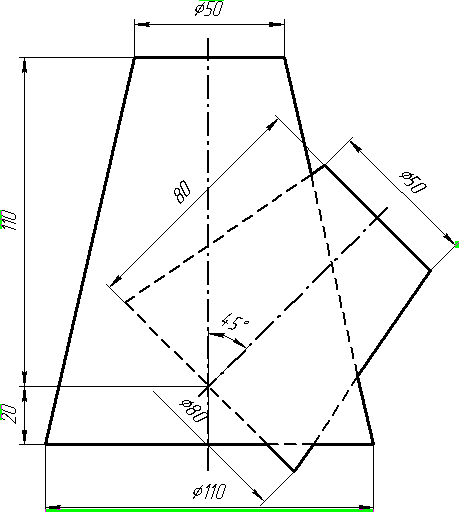
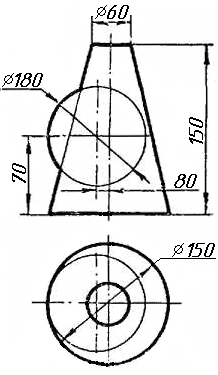
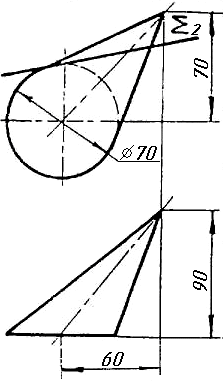
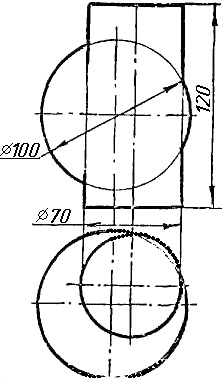
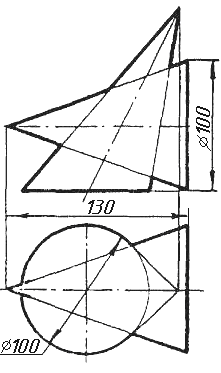
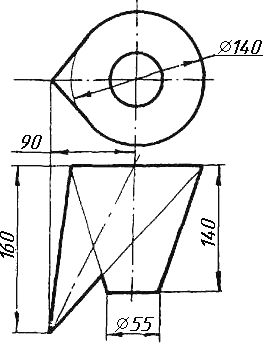
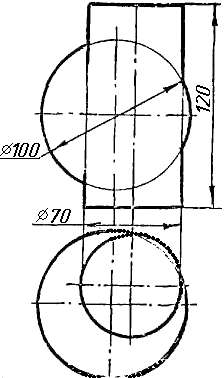
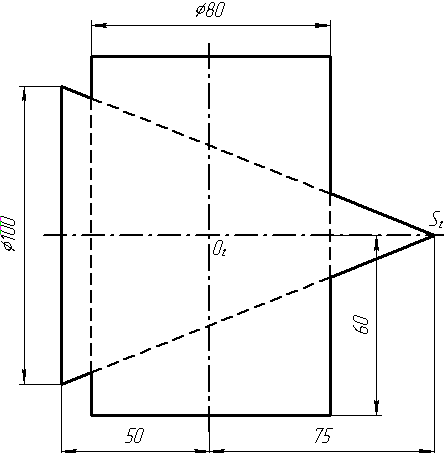
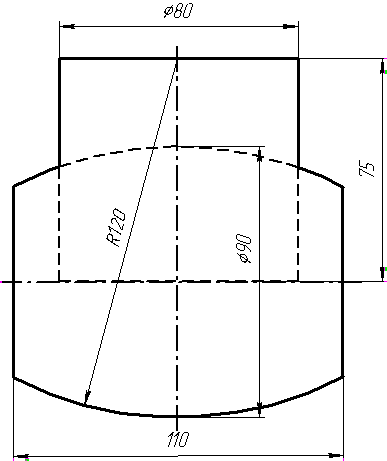
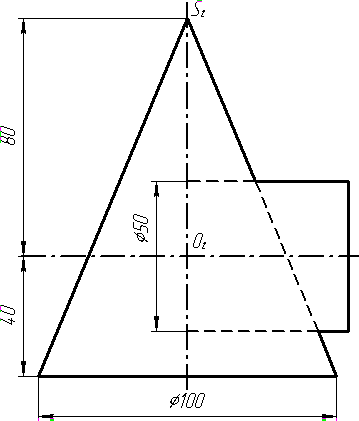
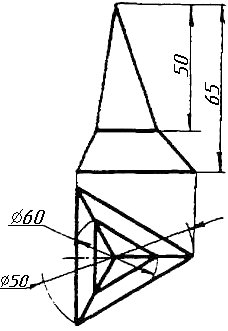
Варіант 1	Завдання 1 x y z A 120 50 5 B 80 50 5 C 80 0 5 K 85 85 20	Завдання 2 x y z A 100 5 75 B 150 5 8 C 80 5 8 K 130 35 50 S 55 110 ?	Завдання 3 x y z A 120 60 0 B 165 15 70 C 100 70 45 K 30 20 25 E 75 75 ? L 105 25 ? Q 40 5 ?
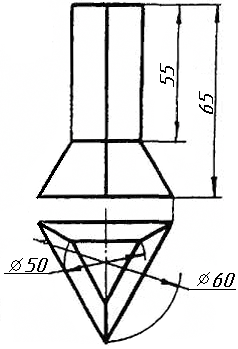
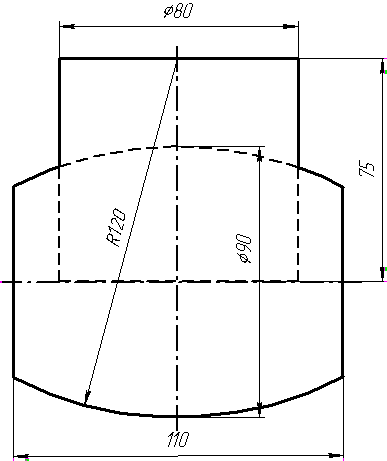
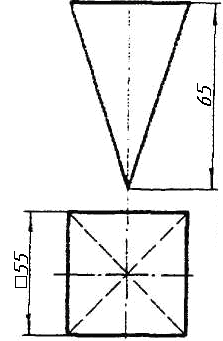
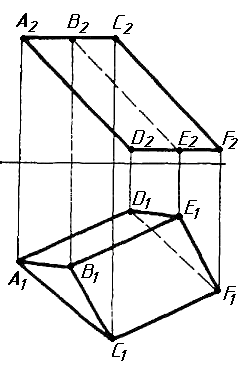
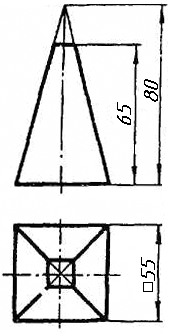
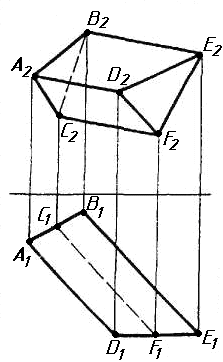
Завдання 0
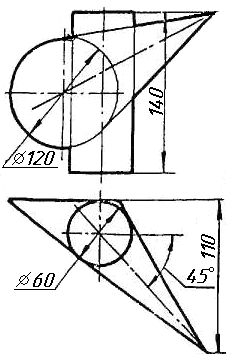
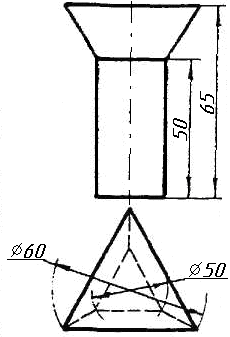
Завдання 4 x y z A 80 95 55 B 10 65 55 C 110 35 0 D 45 10 65 E 0 95 15	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

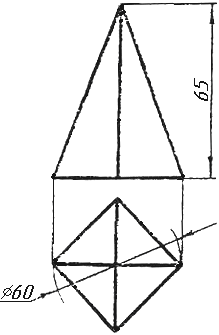
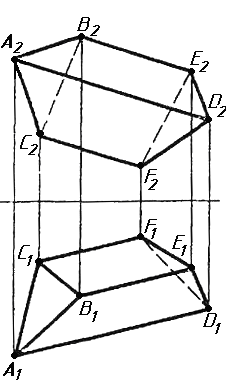
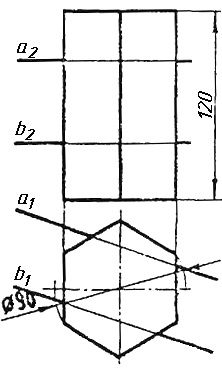
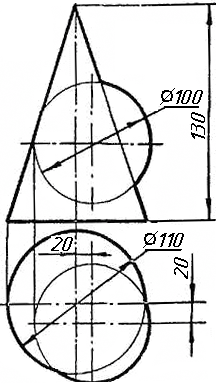
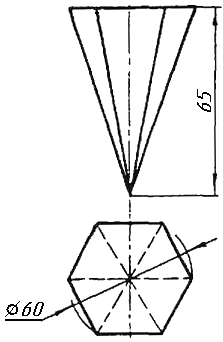
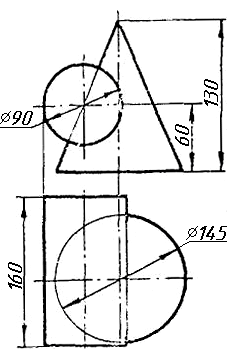
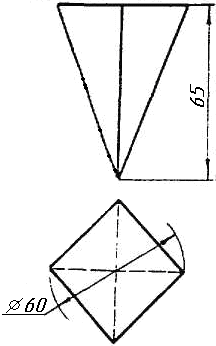
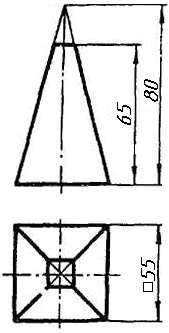
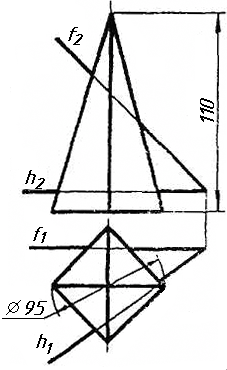
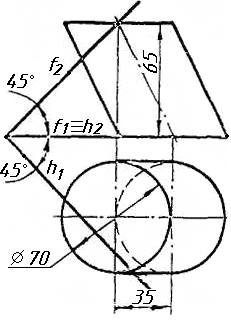
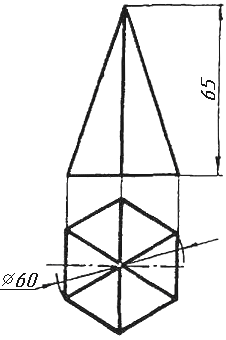
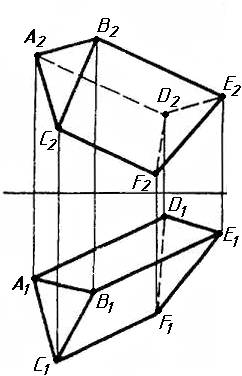
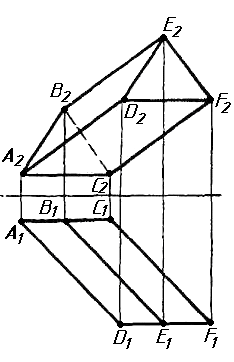
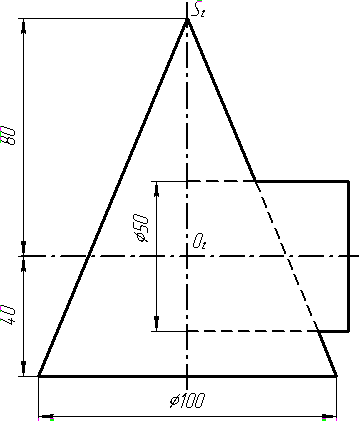
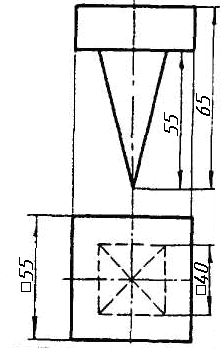
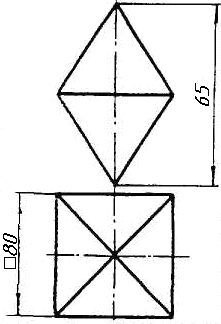
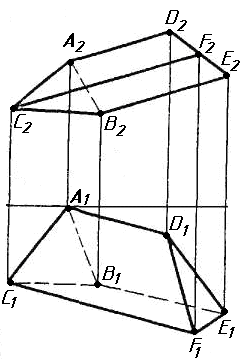
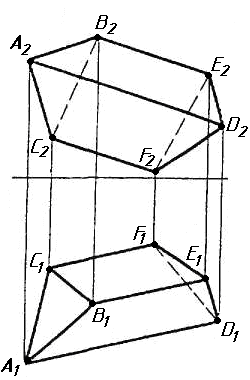
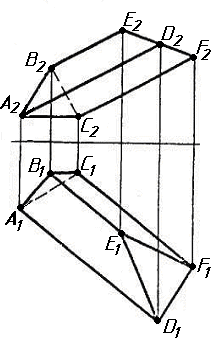
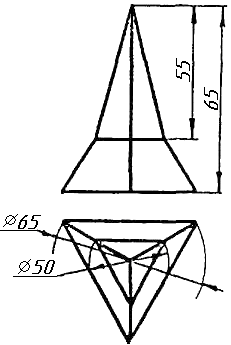
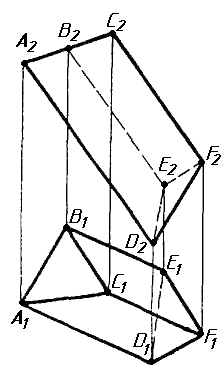
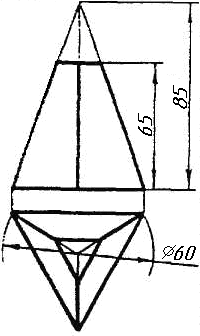
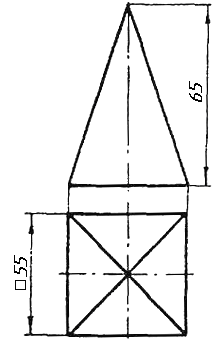
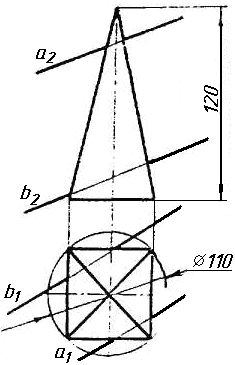
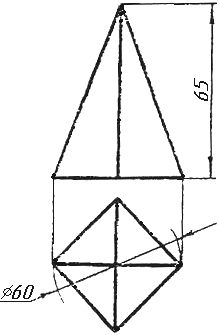
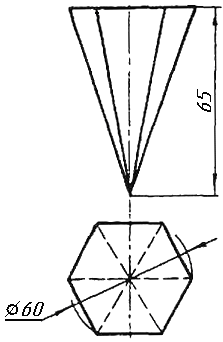
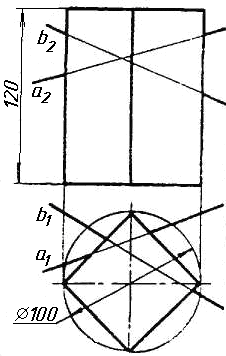
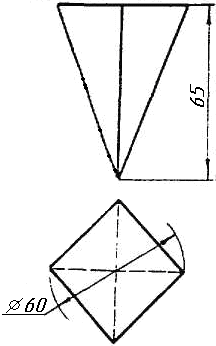
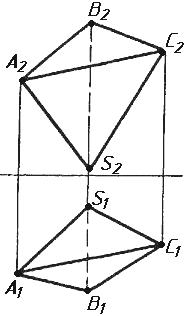
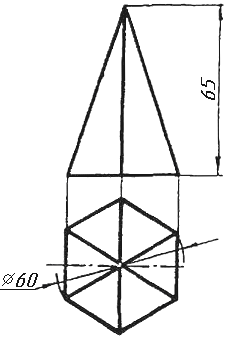
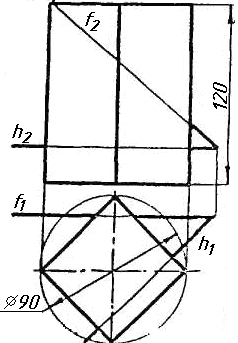
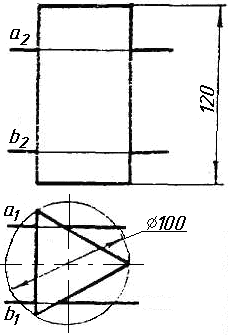
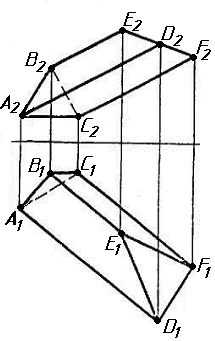
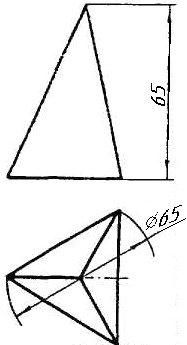
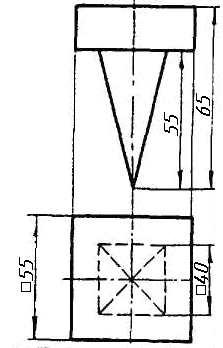
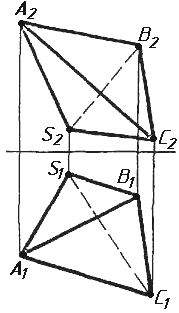
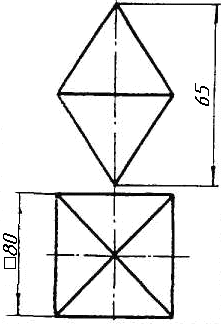
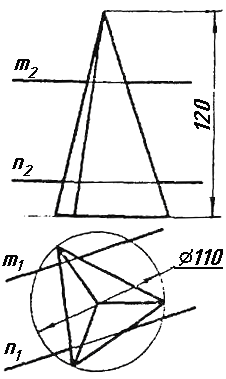
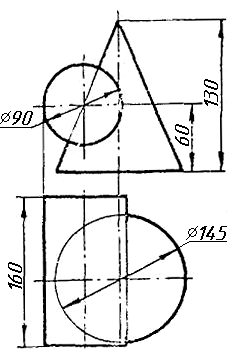
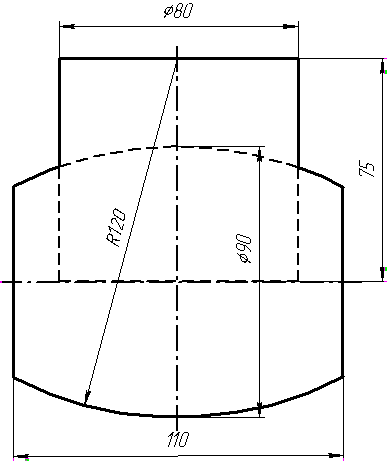
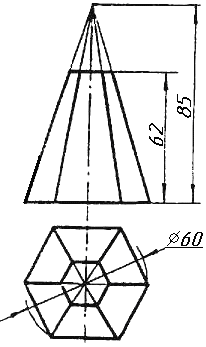
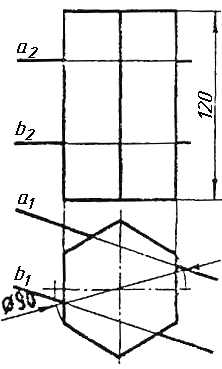
Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

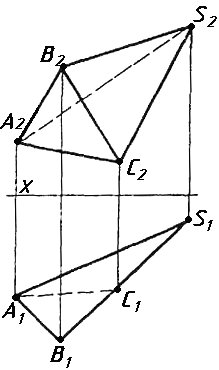
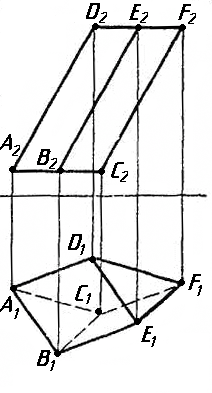
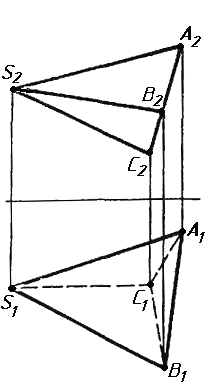
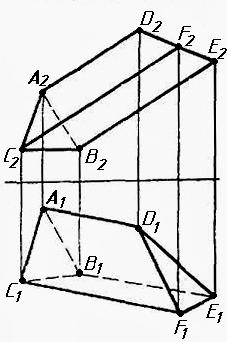
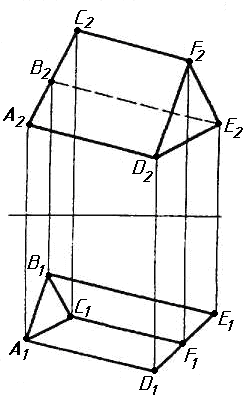
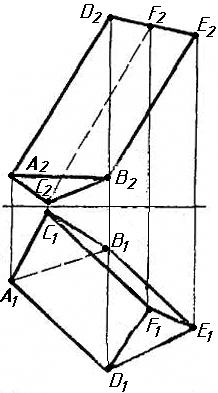
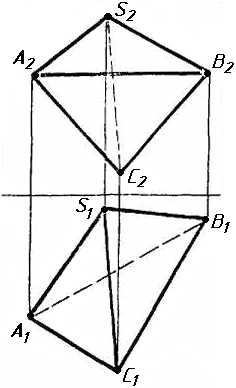
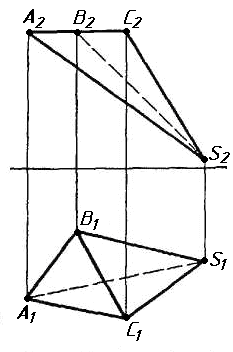
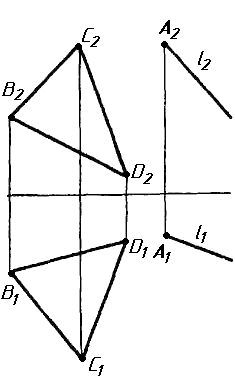
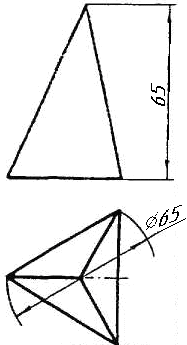
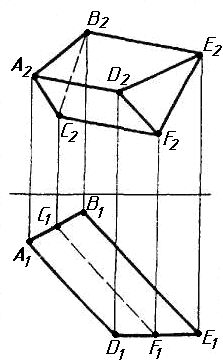
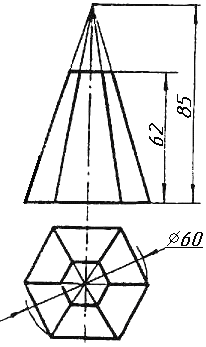
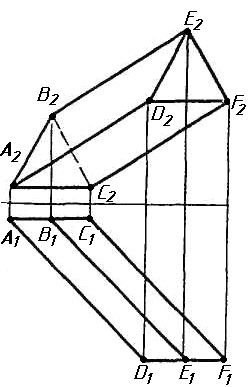
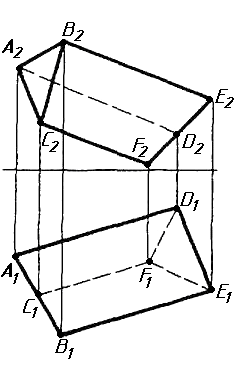
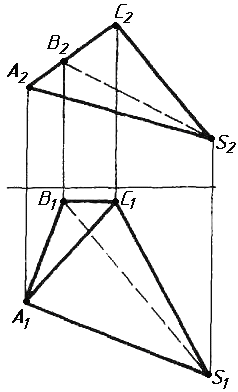
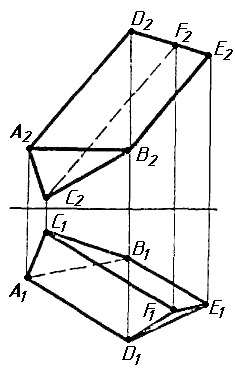
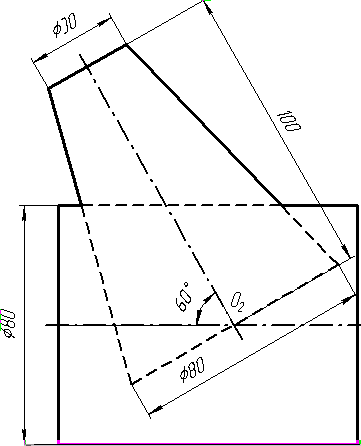
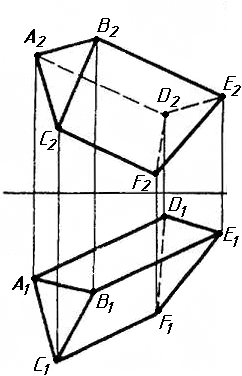
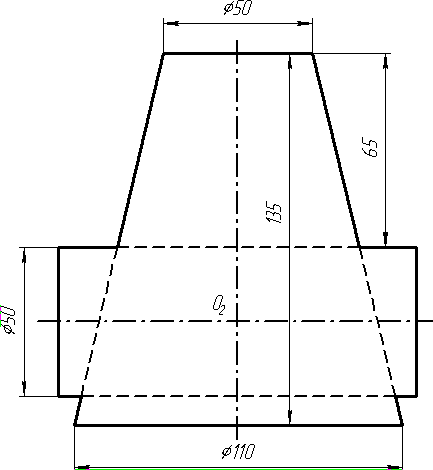
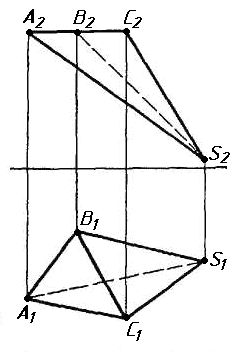
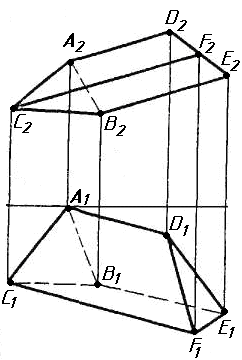
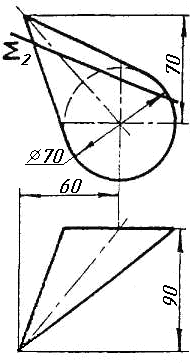
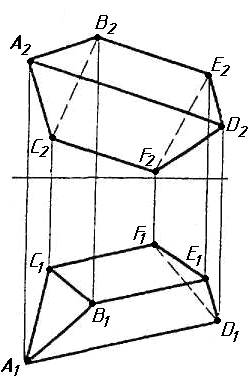
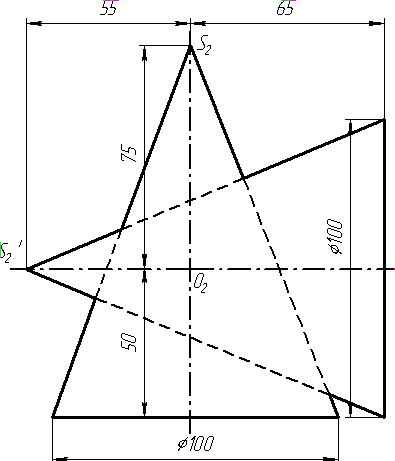
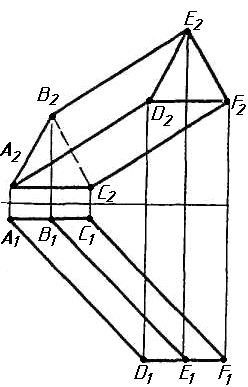
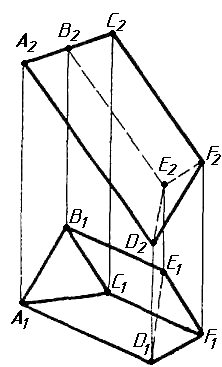
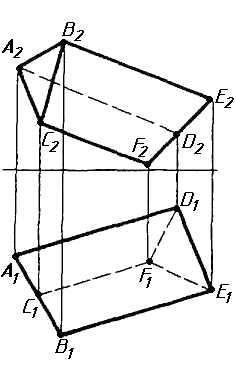
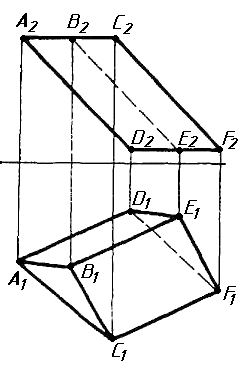
Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

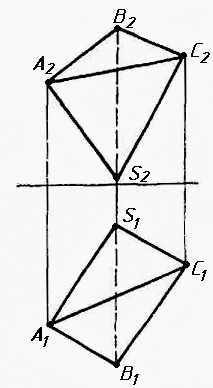
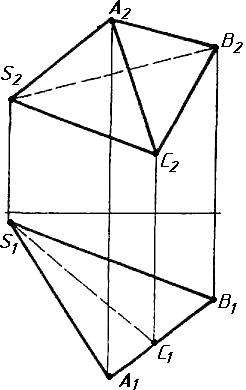
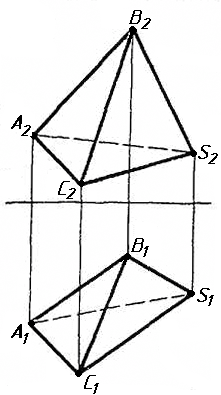
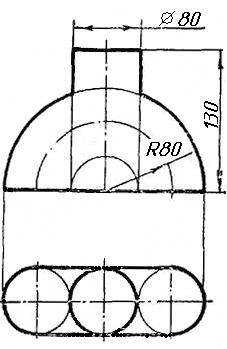
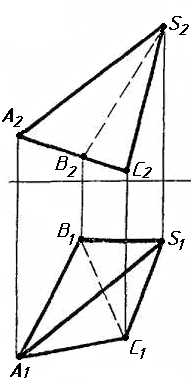
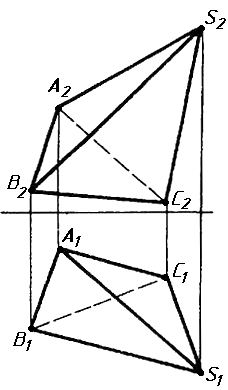
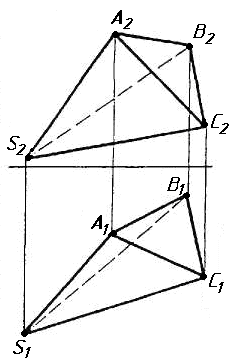
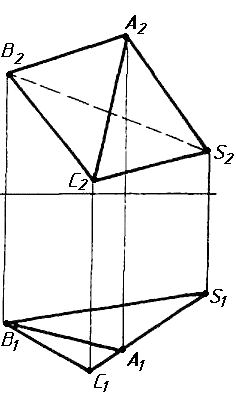
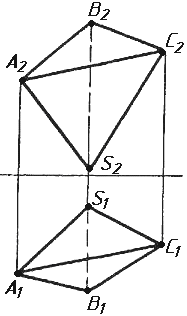
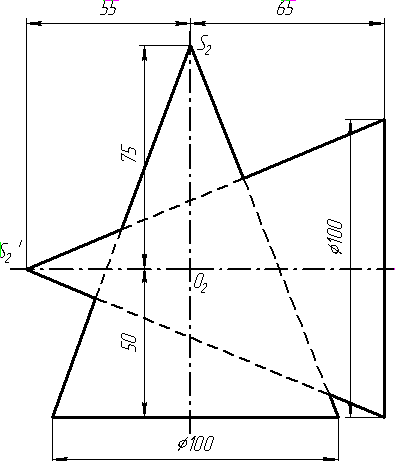
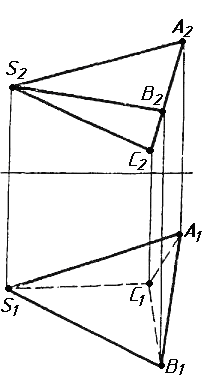
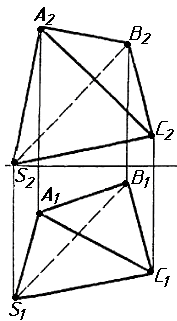
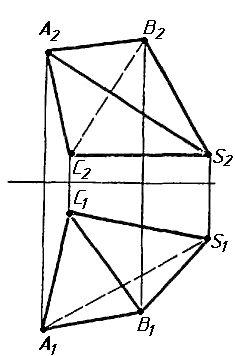
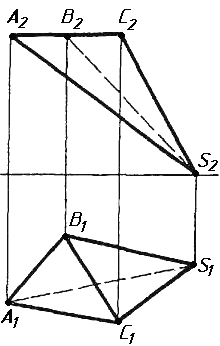
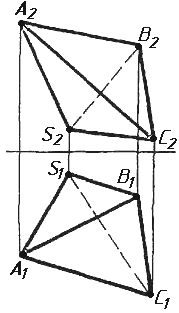
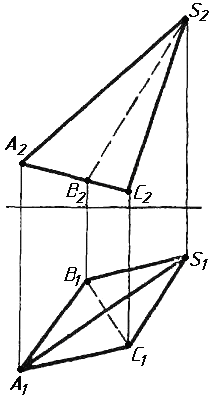
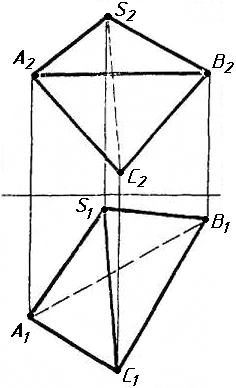
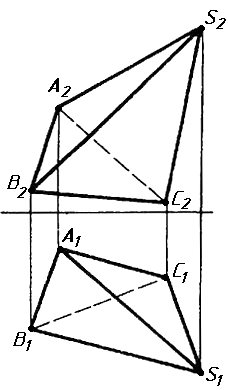
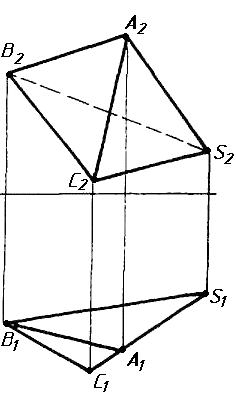
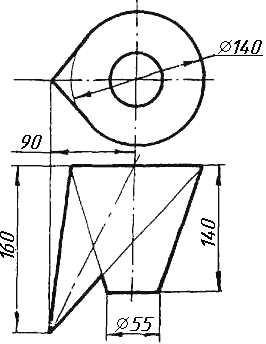
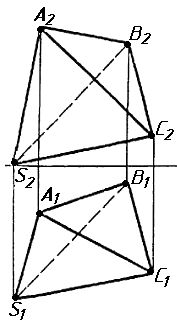
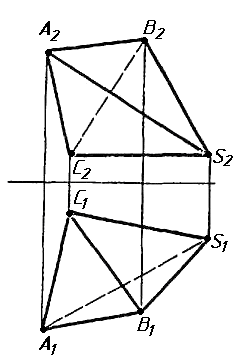
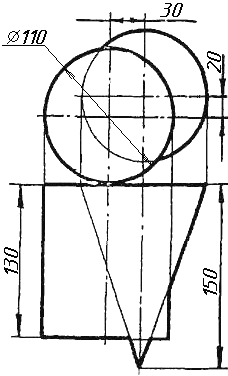
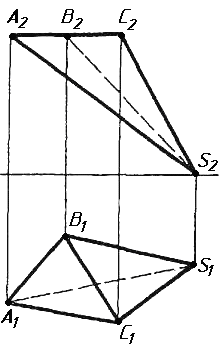
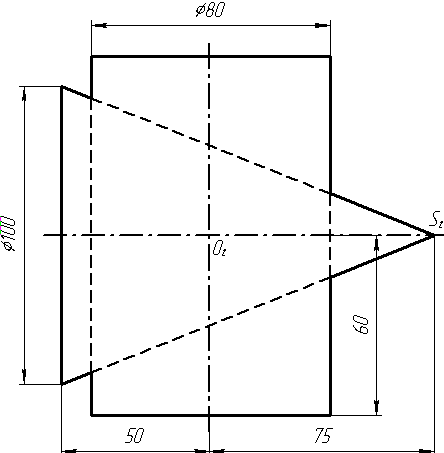
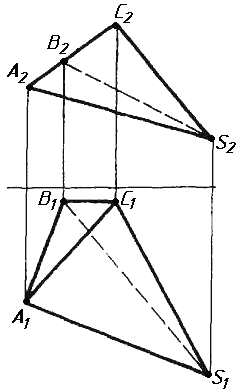
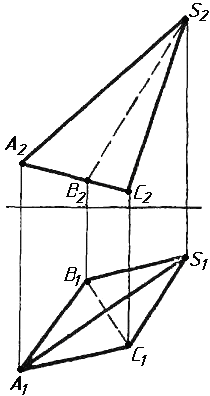
Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

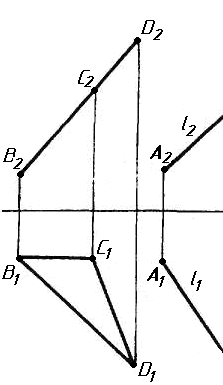
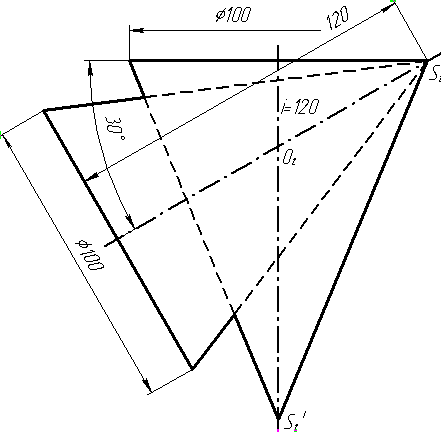
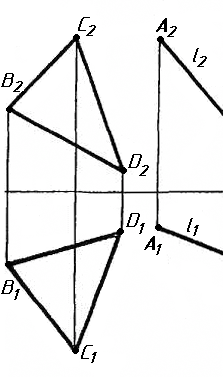
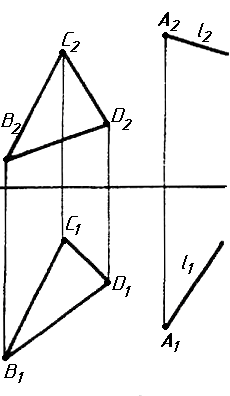
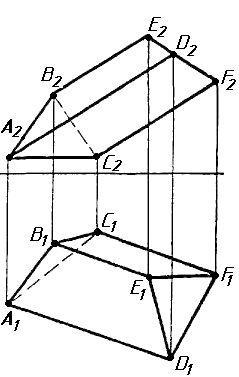
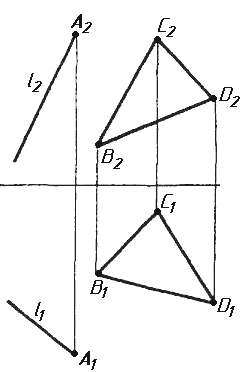
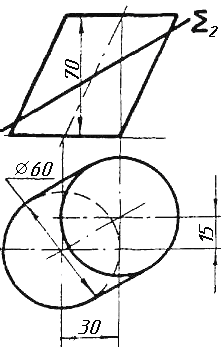
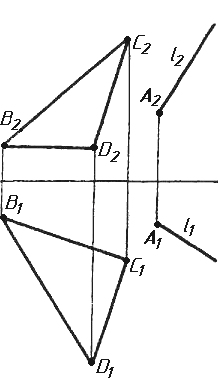
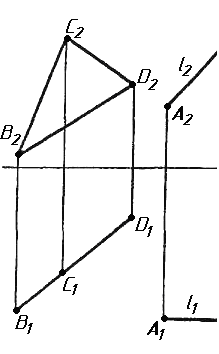
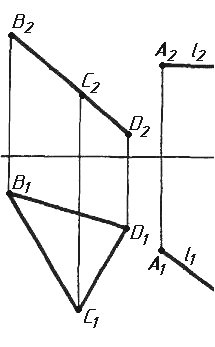
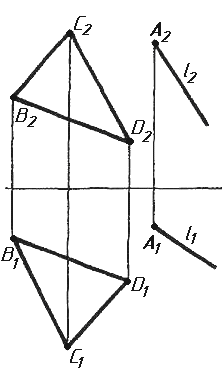
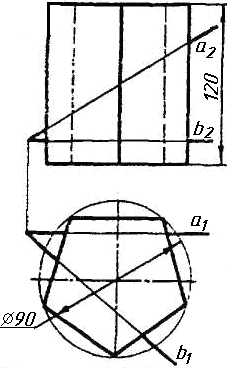
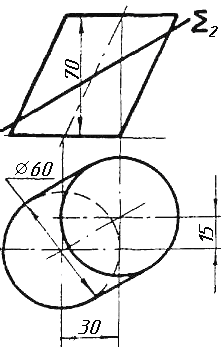
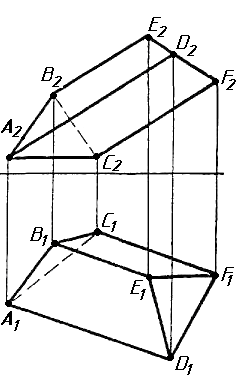
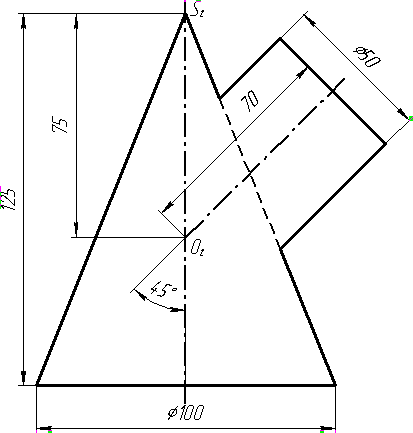
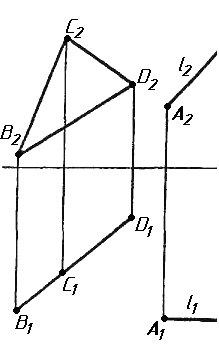
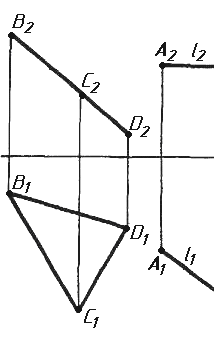
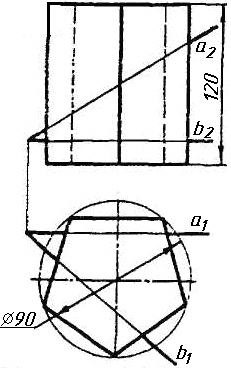
Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

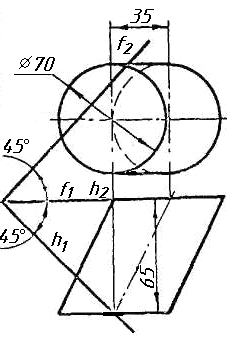
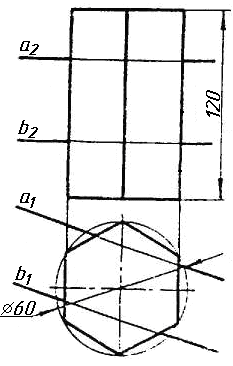
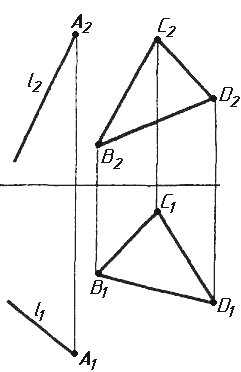
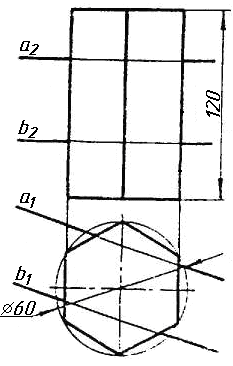
Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P ( CDE). Побудувати лінію перетину двох площин.

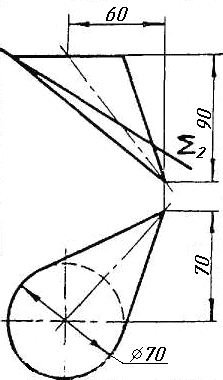
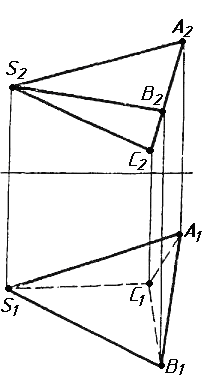
Завдання 5. Визначити кут між гранями ABC та ABS піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AD та BE призми методом плоскопаралельного переміщення.

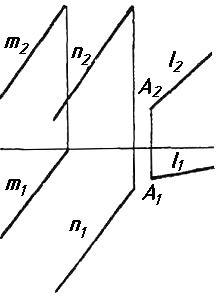
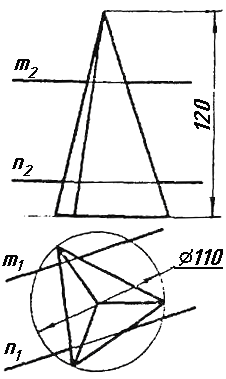
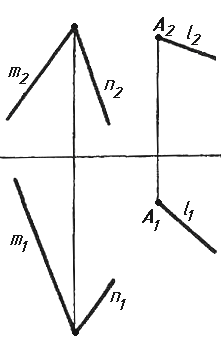
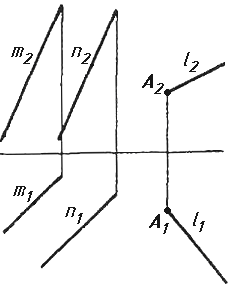
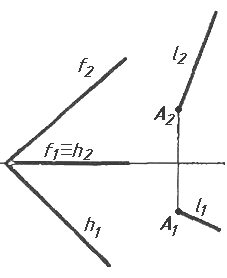
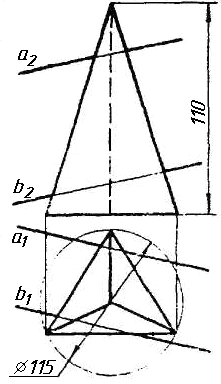
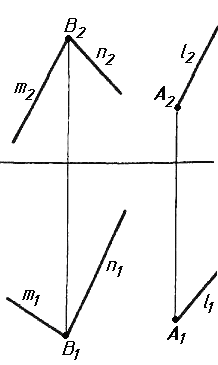
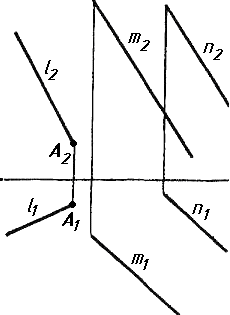
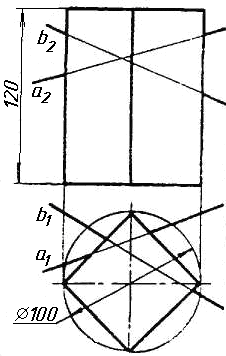
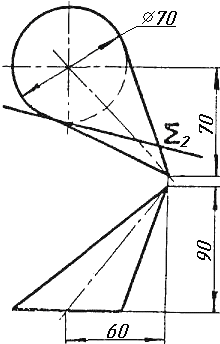
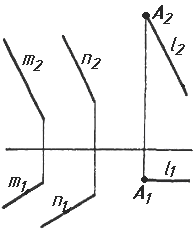
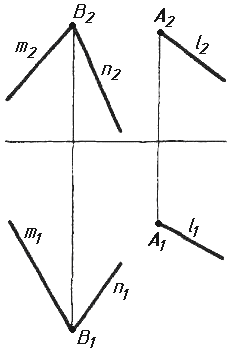
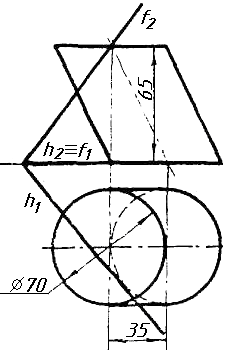
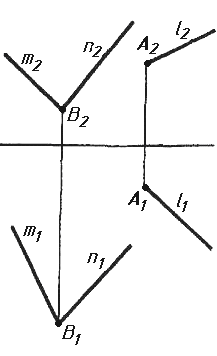
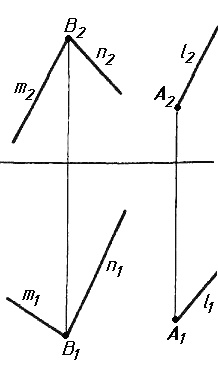
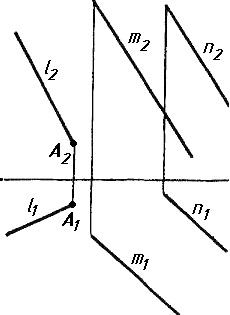
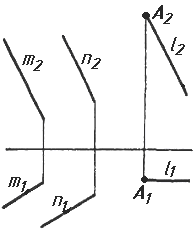
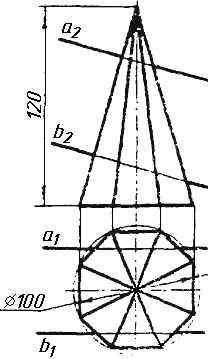
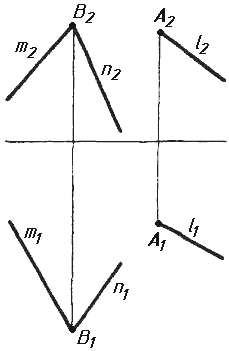
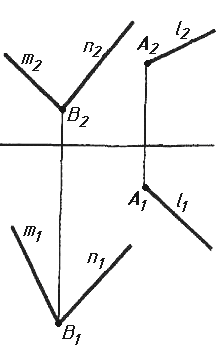
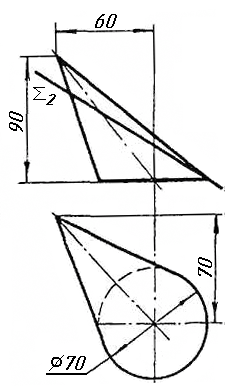
Завдання 7. Визначити натуральну величину кута між прямою l та площиною  (m || n) методом обертання навколо прямої рівня.

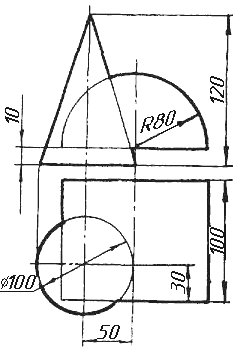
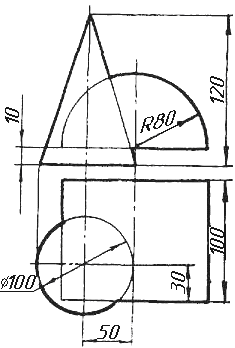
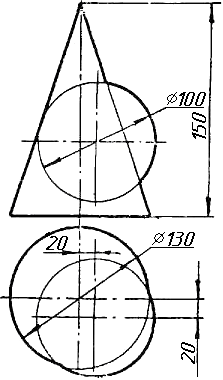
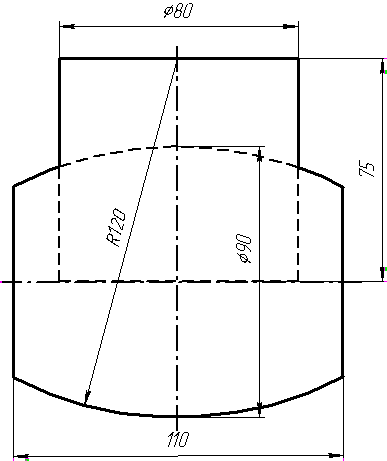
Завдання 8. Побудувати переріз піраміди площиною загального положення.

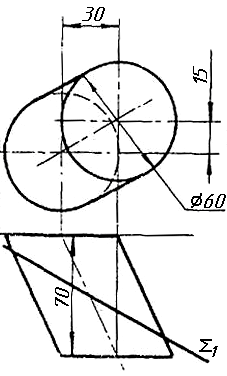
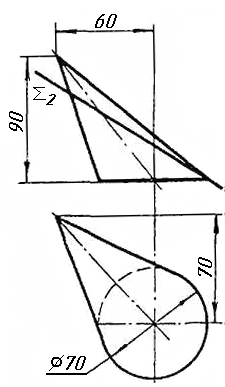
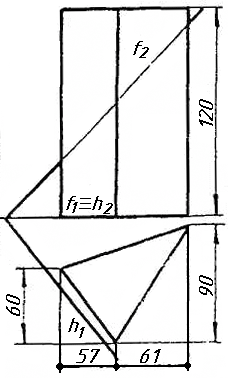
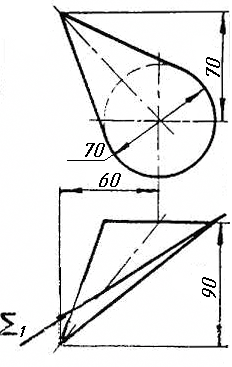
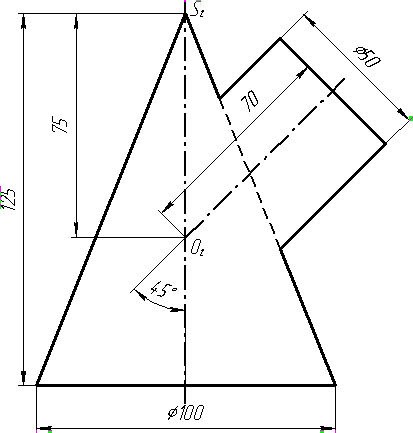
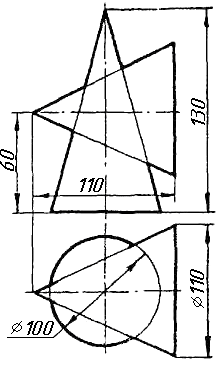
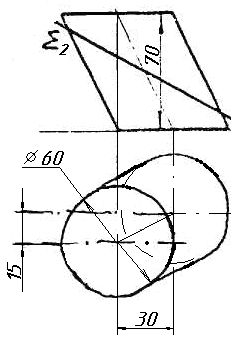
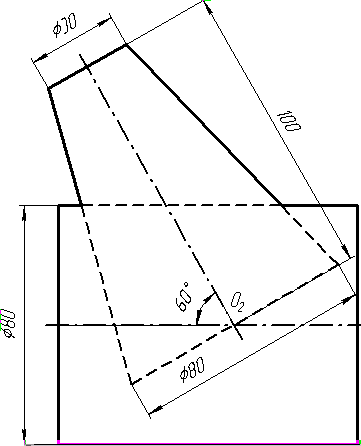
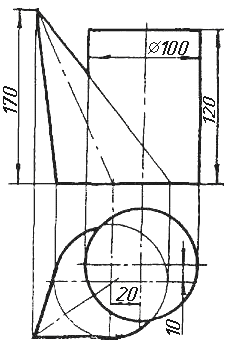
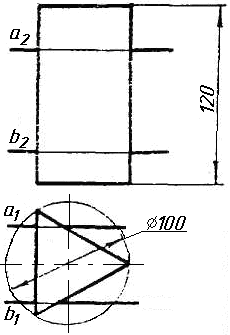
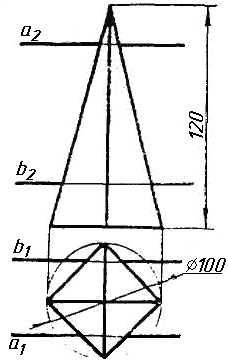
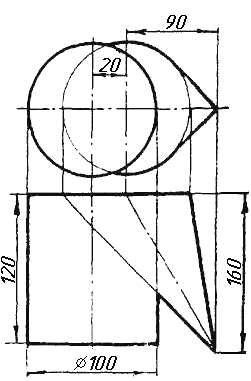
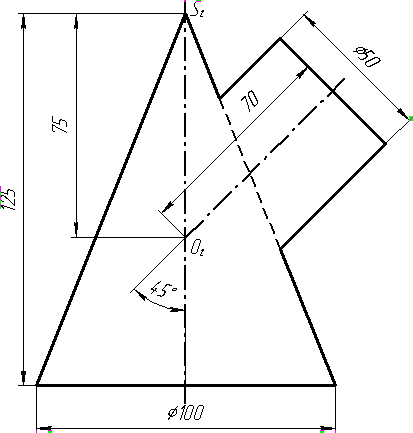
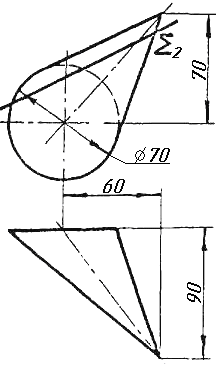
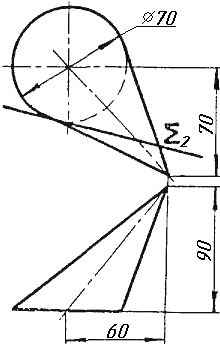
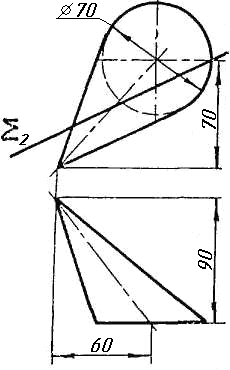
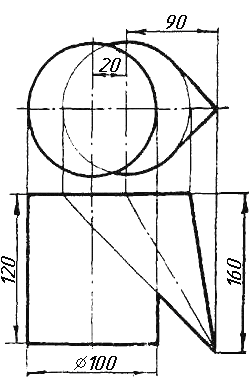
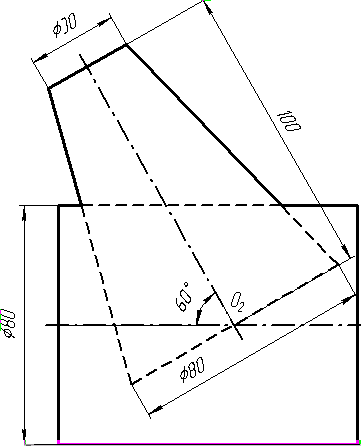
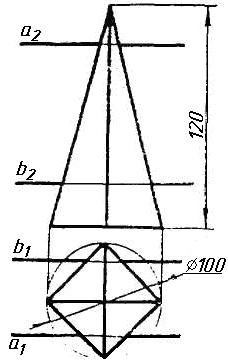
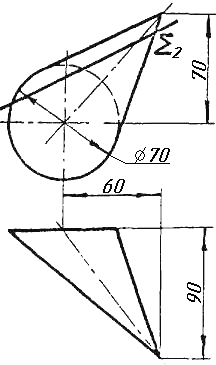
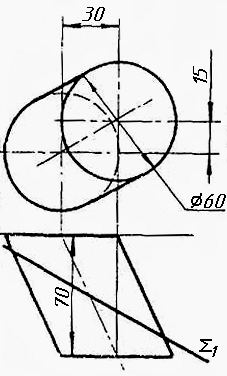
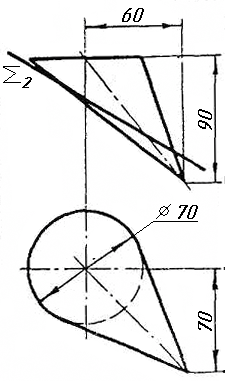
Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

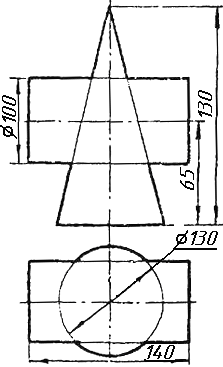
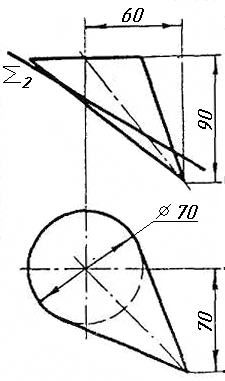
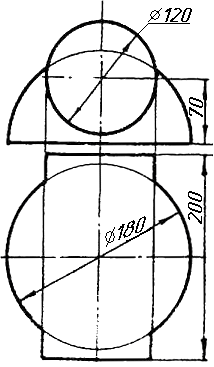
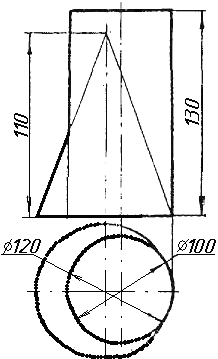
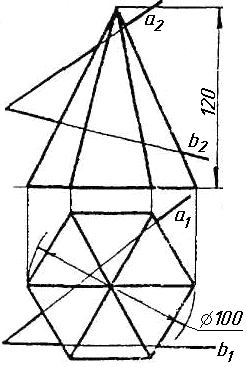
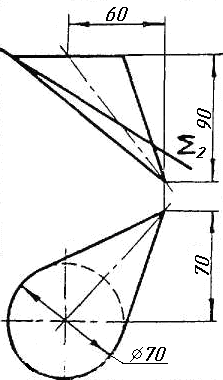
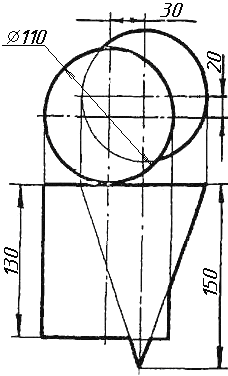
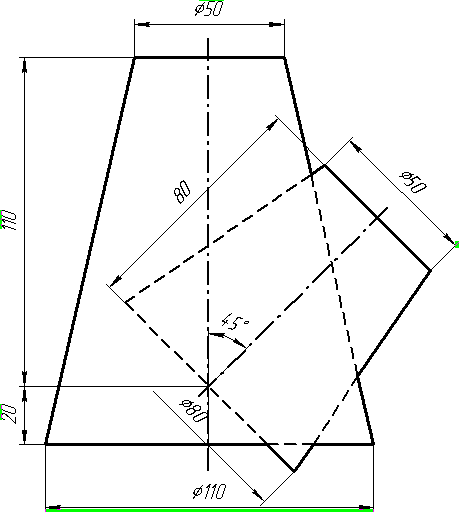
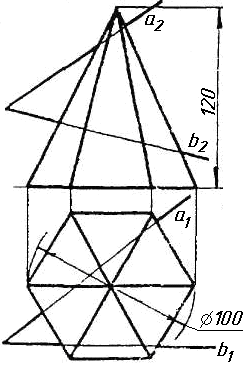
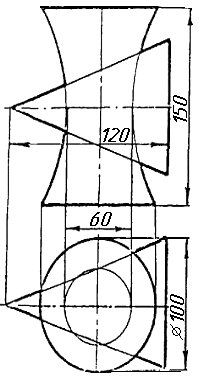
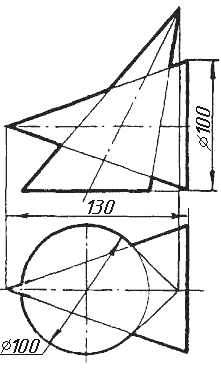
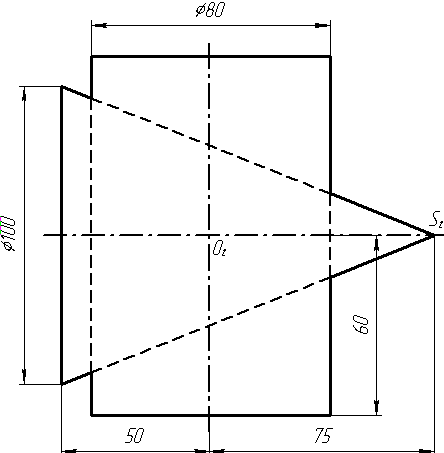
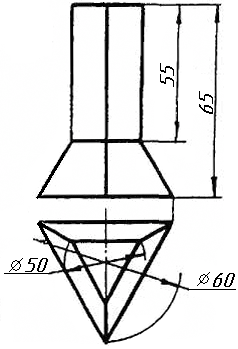
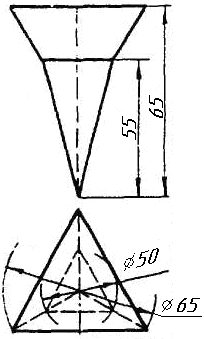
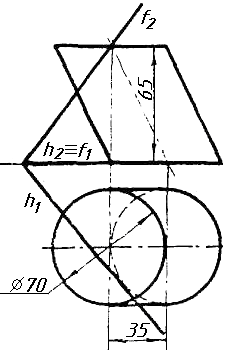
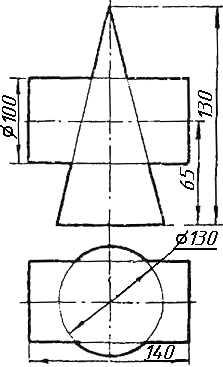
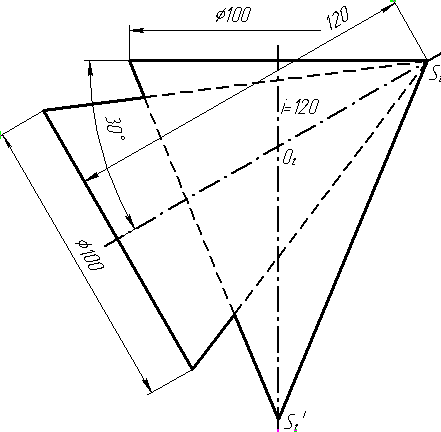
Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях. Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 2	Завдання 1 x y z A 135 5 55 B 115 5 100 C 85 5 100 D 65 5 60 K 100 65 17	Завдання 2 x y z A 115 5 45 B 70 5 90 C 20 5 45 D 70 5 0 K 80 50 50 S 70 ? 45	Завдання 3 x y z A 180 70 50 B 160 75 20 C 145 30 50 K 65 40 60 E 105 ? 80 L 70 ? 0 Q 35 ? 40
Завдання 0
Завдання 4 x y z A 100 0 80 B 0 75 20 C 120 20 25 D 50 80 80 E 15 20 50	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

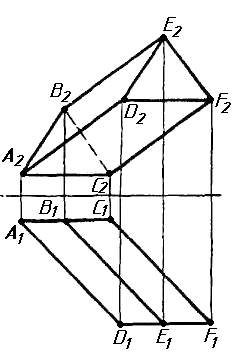
Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини B до ребра АС піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  (m Х n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та сфери. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 3	Завдання 1 x y z A 30 10 22 B 55 10 57 C 90 10 22 K 110 55 75	Завдання 2 x y z A 100 15 35 B 15 32 56 C 48 47 35 K 45 37 55 S 80 ? 95	Завдання 3 x y z A 105 50 0 B 140 0 0 C 170 0 40 K 50 35 60 E 35 80 ? L 0 60 ? Q 60 15 ?
Завдання 0
Завдання 4 x y z A 125 65 10 B 15 20 65 C 145 5 65 D 0 35 0 E 80 85 100	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ASC та BSC піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини D до грані BCFE призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  (m || n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 4	Завдання 1 x y z A 50 40 5 B 80 0 55 C 110 25 5 K 90 90 30	Завдання 2 x y z A 110 120 5 B 55 10 5 C 55 85 5 K 90 60 20 S 175 ? 90	Завдання 3 x y z A 110 25 0 B 160 25 35 C 105 5 25 K 10 40 70 E 140 105 ? L 70 40 ? Q 30 80 ?
Завдання 0
Завдання 4 x y z A 35 90 5 B 90 0 45 C 0 35 15 D 125 0 15 E 95 90 80	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CD; CE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями BCFE та ACFD призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами CB та AS піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину циліндра та тора. Визначити її видимість на двох проекціях.

Варіант 5	Завдання 1 x y z A 125 25 10 B 60 0 10 C 80 55 10 D 105 55 10 K 70 55 100	Завдання 2 x y z A 135 5 20 B 95 5 45 C 60 5 20 K 110 40 50 S 95 ? 85	Завдання 3 x y z A 175 85 0 B 140 45 90 C 120 110 55 K 60 105 35 E 50 45 ? L 90 10 ? Q 105 70 ?
Завдання 0
Завдання 4 x y z A 105 65 40 B 20 35 75 C 115 90 80 D 60 0 10 E 0 100 50	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ACS та BCS піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань від ребра AD до грані BEFC призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  (f; h) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину циліндра та тора. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 6	Завдання 1 x y z A 155 12 10 B 100 12 10 C 135 50 10 K 120 35 65	Завдання 2 x y z A 100 75 5 B 150 8 5 C 80 8 5 K 130 50 35 S 55 ? 110	Завдання 3 x y z A 140 65 30 B 120 20 0 C 95 0 8 K 25 30 45 E 70 60 ? L 35 10 ? Q 0 45 ?
Завдання 0
Завдання 4 x y z A 90 90 80 B 20 60 30 C 115 25 50 D 35 25 75 E 0 100 15	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ || СD).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CD; CE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABC та ABS піраміди методом заміни площин проекцій.

Завдання 6. Визначити натуральну величину перпендикуляра між ребрами AВ та SC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та сфери. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину циліндра та конуса. Визначити її видимість на двох проекціях.

Варіант 7	Завдання 1 x y z A 130 10 0 B 70 10 20 C 155 45 35 K 72 65 35	Завдання 2 x y z A 10 5 10 B 40 50 85 C 40 50 10 K 115 55 70 S 165 ? 90	Завдання 3 x y z A 165 85 60 B 145 45 115 C 115 85 90 K 120 0 70 E 80 60 ? L 20 90 ? Q 55 35 ?
Завдання 0
Завдання 4 x y z A 55 100 45 B 90 0 15 C 100 0 80 D 80 50 0 E 0 75 20	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CD; DE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AS та BC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину півсфери та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 8	Завдання 1 x y z A 135 10 25 B 60 10 25 C 35 10 55 K 120 50 35	Завдання 2 x y z A 75 10 10 B 115 85 10 C 165 10 10 K 160 45 30 S 125 ? 90	Завдання 3 x y z A 180 50 70 B 165 20 75 C 145 50 30 K 85 60 40 E 105 80 ? L 70 0 ? Q 40 45 ?
Завдання 0
Завдання 4 x y z A 70 30 30 B 135 100 30 C 115 15 0 D 50 30 95 E 165 90 70	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABC та ABS піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами CF та BE призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса з циліндром. Визначити її видимість на двох проекціях.

Варіант 9	Завдання 1 x y z A 150 20 10 B 95 50 10 C 75 15 10 K 115 50 45	Завдання 2 x y z A 140 20 5 B 105 10 5 C 75 75 5 K 85 30 40 S 40 55 90	Завдання 3 x y z A 120 0 65 B 165 75 15 C 180 45 70 K 85 60 40 E 35 ? 5 L 70 ? 75 Q 105 ? 25
Завдання 0
Завдання 4 x y z A 45 30 75 B 65 105 55 C 95 115 75 D 0 35 45 E 90 50 25	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CD; DE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями SAC та BAC піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами CF та BE призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P (m; n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 10	Завдання 1 x y z A 120 5 25 B 95 5 70 C 45 5 10 K 90 55 45	Завдання 2 x y z A 160 10 55 B 110 10 10 C 60 10 85 K 115 40 40 S 90 90 ?	Завдання 3 x y z A 30 115 45 B 10 60 85 C 60 90 85 K 110 65 15 E 115 ? 90 L 120 ? 35 Q 95 ? 60
Завдання 0
Завдання 4 x y z A 100 80 0 B 0 20 75 C 120 25 20 D 50 80 80 E 15 50 20	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CD; CE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AS та BC призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса з тором. Визначити її видимість на двох проекціях.

Варіант 11	Завдання 1 x y z A 145 30 5 B 110 50 5 C 95 20 5 K 100 65 55	Завдання 2 x y z A 140 10 0 B 65 10 30 C 140 10 80 K 75 35 40 S 40 90 ?	Завдання 3 x y z A 120 20 0 B 140 65 30 C 95 0 8 K 25 30 45 E 0 ? 90 L 35 ? 20 Q 70 ? 25
Завдання 0
Завдання 4 x y z A 95 75 60 B 0 0 60 C 130 10 75 D 55 55 0 E 75 20 100	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; С).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити відстань від вершини A до грані CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити кут між гранями ВAС та SAC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  (m || n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 12	Завдання 1 x y z A 155 10 12 B 100 10 12 C 135 10 50 K 120 65 35	Завдання 2 x y z A 135 20 5 B 95 45 5 C 60 20 5 K 110 50 40 S 95 85 ?	Завдання 3 x y z A 115 90 85 B 165 60 85 C 145 115 45 K 120 70 0 E 80 30 ? L 20 30 ? Q 55 75 ?
Завдання 0
Завдання 4 x y z A 60 25 75 B 125 115 0 C 115 80 90 D 60 10 0 E 0 50 90	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; С).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (C; DE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини В до ребра AS піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та сфери. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 13	Завдання 1 x y z A 160 5 5 B 95 5 5 C 160 55 5 K 120 25 70	Завдання 2 x y z A 75 10 10 B 115 10 85 C 165 10 10 K 100 30 45 S 125 90 ?	Завдання 3 x y z A 145 45 115 B 115 85 90 C 165 85 60 K 100 15 65 E 20 ? 30 L 80 ? 30 Q 55 ? 75
Завдання 0
Завдання 4 x y z A 90 80 105 B 0 0 50 C 0 10 100 D 70 85 0 E 110 10 60	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  ( АВC).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями BADE та CADF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AB та CF піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  (m || n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та тора. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 14	Завдання 1 x y z A 145 50 10 B 90 50 10 C 145 5 10 K 100 75 70	Завдання 2 x y z A 145 10 10 B 75 45 10 C 145 80 10 K 100 40 40 S 110 ? 90	Завдання 3 x y z A 70 0 25 B 20 35 25 C 75 25 5 K 170 70 40 E 40 50 ? L 110 110 ? Q 150 10 ?
Завдання 0
Завдання 4 x y z A 130 75 100 B 0 70 70 C 140 10 30 D 70 10 105 E 40 100 30	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; С).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини S до ребра BC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину сфери та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину циліндра та тора. Визначити її видимість на двох проекціях.

Варіант 15	Завдання 1 x y z A 75 15 35 B 100 65 0 C 125 25 0 K 95 40 65	Завдання 2 x y z A 100 90 30 B 60 90 87 C 25 90 30 K 115 57 35 S 170 0 ?	Завдання 3 x y z A 145 115 45 B 165 60 85 C 115 90 85 K 100 65 15 E 20 ? 90 L 55 ? 35 Q 80 ? 60
Завдання 0
Завдання 4 x y z A 125 110 70 B 35 65 55 C 85 0 85 D 20 125 40 E 155 65 0	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (А, В, С).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CE, D). Побудувати лінію перетину двох площин.

Завдання 5. Визначити відстань між ребрами AD та BE призми методом плоскопаралельного переміщення.

Завдання 6. Визначити кут між гранями ABC та ABS піраміди методом заміни площин проекцій.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 16	Завдання 1 x y z A 145 10 10 B 145 70 10 C 80 40 10 K 130 28 40	Завдання 2 x y z A 110 10 60 B 60 10 15 C 35 10 60 K 85 10 90 S 65 90 ?	Завдання 3 x y z A 160 35 25 B 110 0 25 C 105 25 5 K 20 65 45 E 30 10 ? L 140 50 ? Q 70 110 ?
Завдання 0
Завдання 4 x y z A 45 35 20 B 150 50 60 C 125 0 85 D 160 65 0 E 20 120 55	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  ( АВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  (C, D, E). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та BEFC призми методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини S до ребра AB піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 17	Завдання 1 x y z A 150 25 20 B 115 55 0 C 70 5 20 K 115 43 40	Завдання 2 x y z A 160 17 7 B 105 5 28 C 160 17 70 K 85 50 55 S 45 90 ?	Завдання 3 x y z A 60 85 90 B 10 85 60 C 30 45 115 K 75 15 65 E 95 ? 30 L 155 ? 20 Q 120 ? 75
Завдання 0
Завдання 4 x y z A 35 115 85 B 110 20 0 C 105 65 40 D 20 35 75 E 45 80 0	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  ( АВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями BEDA та BEFC призми методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини S до ребра АВ піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною Р (m Х n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 18	Завдання 1 x y z A 150 0 10 B 150 35 10 C 90 0 10 K 120 17 40	Завдання 2 x y z A 90 90 30 B 120 15 65 C 160 90 30 K 80 30 75 S 30 ? 90	Завдання 3 x y z A 75 5 25 B 70 25 0 C 20 25 35 K 170 40 70 E 110 40 ? L 40 105 ? Q 150 80 ?
Завдання 0
Завдання 4 x y z A 135 90 90 B 0 65 50 C 20 80 80 D 95 0 110 E 150 30 70	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; С).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  (CD; СE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити відстань від ребра AD до грані CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити кут між гранями ABC та ABS піраміди методом плоско паралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною  (m; n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 19	Завдання 1 x y z A 135 5 55 B 115 5 100 C 85 5 100 D 65 5 60 K 100 65 17	Завдання 2 x y z A 100 15 35 B 15 32 56 C 48 47 35 K 45 37 55 S 80 ? 95	Завдання 3 x y z A 110 25 0 B 160 25 35 C 105 5 25 K 10 40 70 E 140 105 ? L 70 40 ? Q 30 80 ?
Завдання 0
Завдання 4 x y z A 105 65 40 B 20 35 75 C 115 90 80 D 60 0 10 E 0 100 50	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABC та ABS піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AC та BS піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 20	Завдання 1 x y z A 30 10 22 B 55 10 57 C 90 10 22 K 110 55 75	Завдання 2 x y z A 110 120 5 B 55 10 5 C 55 85 5 K 90 60 20 S 175 ? 90	Завдання 3 x y z A 175 85 0 B 140 45 90 C 120 110 55 K 60 105 35 E 50 45 ? L 90 10 ? Q 105 70 ?
Завдання 0
Завдання 4 x y z A 90 90 80 B 20 60 30 C 115 25 50 D 35 25 75 E 0 100 15	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини Р (CD; СE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами CF та BE призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P (m X n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та сфери. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 21	Завдання 1 x y z A 50 40 5 B 80 0 55 C 110 25 5 K 90 90 30	Завдання 2 x y z A 135 5 20 B 95 5 45 C 60 5 20 K 110 40 50 S 95 ? 85	Завдання 3 x y z A 140 65 30 B 120 20 0 C 95 0 8 K 25 30 45 E 70 60 ? L 35 10 ? Q 0 45 ?
Завдання 0
Завдання 4 x y z A 55 100 45 B 90 0 15 C 100 0 80 D 80 50 0 E 0 75 20	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ || ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CD; DE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABC та ABS піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами CF та BE призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та тора. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину циліндра та тора. Визначити її видимість на двох проекціях.

Варіант 22	Завдання 1 x y z A 125 25 10 B 60 0 10 C 80 55 10 D 105 55 10 K 70 55 100	Завдання 2 x y z A 100 75 5 B 150 8 5 C 80 8 5 K 130 50 35 S 55 ? 110	Завдання 3 x y z A 165 85 60 B 145 45 115 C 115 85 90 K 120 0 70 E 80 60 ? L 20 90 ? Q 55 35 ?
Завдання 0
Завдання 4 x y z A 70 30 30 B 135 100 30 C 115 15 0 D 50 30 95 E 165 90 70	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  ( АВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями SAC та BAC піраміди методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AS та BC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P (m || n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину сфери та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 23	Завдання 1 x y z A 155 12 10 B 100 12 10 C 135 50 10 K 120 35 65	Завдання 2 x y z A 10 5 10 B 40 50 85 C 40 50 10 K 115 55 70 S 165 ? 90	Завдання 3 x y z A 180 50 70 B 165 20 75 C 145 50 30 K 85 60 40 E 105 80 ? L 70 0 ? Q 40 45 ?
Завдання 0
Завдання 4 x y z A 45 30 75 B 65 105 55 C 95 115 75 D 0 35 45 E 90 50 25	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини P (CD; DE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AS та BC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною Р ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 24	Завдання 1 x y z A 130 10 0 B 70 10 20 C 155 45 35 K 72 65 35	Завдання 2 x y z A 75 10 10 B 115 85 10 C 165 10 10 K 160 45 30 S 125 ? 90	Завдання 3 x y z A 120 0 65 B 165 75 15 C 180 45 70 K 85 60 40 E 35 ? 5 L 70 ? 75 Q 105 ? 25
Завдання 0
Завдання 4 x y z A 100 80 0 B 0 20 75 C 120 25 20 D 50 80 80 E 15 50 20	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини Р (CD; СE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити відстань від вершини A до грані CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити кут між гранями ABS та BCS піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною Р (m || n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 25	Завдання 1 x y z A 135 10 25 B 60 10 25 C 35 10 55 K 120 50 35	Завдання 2 x y z A 140 20 5 B 105 10 5 C 75 75 5 K 85 30 40 S 40 55 90	Завдання 3 x y z A 30 115 45 B 10 60 85 C 60 90 85 K 110 65 15 E 115 ? 90 L 120 ? 35 Q 95 ? 60
Завдання 0
Завдання 4 x y z A 95 75 60 B 0 0 60 C 130 10 75 D 55 55 0 E 75 20 100	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини Р ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AB та CS призми методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 26	Завдання 1 x y z A 150 20 10 B 95 50 10 C 75 15 10 K 115 50 45	Завдання 2 x y z A 160 10 55 B 110 10 10 C 60 10 85 K 115 40 40 S 90 90 ?	Завдання 3 x y z A 120 20 0 B 140 65 30 C 95 0 8 K 25 30 45 E 0 ? 90 L 35 ? 20 Q 70 ? 25
Завдання 0
Завдання 4 x y z A 130 75 100 B 0 70 70 C 140 10 30 D 70 10 105 E 40 100 30	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; С).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями BADE та CADF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини S до ребра BC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 27	Завдання 1 x y z A 120 5 25 B 95 5 70 C 45 5 10 K 90 55 45	Завдання 2 x y z A 140 10 0 B 65 10 30 C 140 10 80 K 75 35 40 S 40 90 ?	Завдання 3 x y z A 115 90 85 B 165 60 85 C 145 115 45 K 120 70 0 E 80 30 ? L 20 30 ? Q 55 75 ?
Завдання 0
Завдання 4 x y z A 90 80 105 B 0 0 50 C 0 10 100 D 70 85 0 E 110 10 60	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій.

Завдання 6. Визначити відстань від вершини S до ребра BC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.

Варіант 28	Завдання 1 x y z A 145 30 5 B 110 50 5 C 95 20 5 K 100 65 55	Завдання 2 x y z A 135 20 5 B 95 45 5 C 60 20 5 K 110 50 40 S 95 85 ?	Завдання 3 x y z A 145 45 115 B 115 85 90 C 165 85 60 K 100 15 65 E 20 ? 30 L 80 ? 30 Q 55 ? 75
Завдання 0
Завдання 4 x y z A 130 75 100 B 0 70 70 C 140 10 30 D 70 10 105 E 40 100 30	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  ( АВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити відстань між ребрами AD та BE призми методом плоско паралельного переміщення.

Завдання 6. Визначити кут між гранями ABS та ABC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною P (m X n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та сфери. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.

Варіант 29	Завдання 1 x y z A 155 10 12 B 100 10 12 C 135 10 50 K 120 65 35	Завдання 2 x y z A 75 10 10 B 115 10 85 C 165 10 10 K 100 30 45 S 125 90 ?	Завдання 3 x y z A 70 0 25 B 20 35 25 C 75 25 5 K 170 70 40 E 40 50 ? L 110 110 ? Q 150 10 ?
Завдання 0
Завдання 4 x y z A 125 110 70 B 35 65 55 C 85 0 85 D 20 125 40 E 155 65 0	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (АВ; ВС).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини Р (CЕ; D). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями ABED та BEFC призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AC та BS піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною Р (m Х n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз піраміди площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину циліндра та тора. Визначити її видимість на двох проекціях.

Варіант 30	Завдання 1 x y z A 155 10 12 B 100 10 12 C 135 10 50 K 120 65 35	Завдання 2 x y z A 145 10 10 B 75 45 10 C 145 80 10 K 100 40 40 S 110 ? 90	Завдання 3 x y z A 145 115 45 B 165 60 85 C 115 90 85 K 100 65 15 E 20 ? 90 L 55 ? 35 Q 80 ? 60
Завдання 0
Завдання 4 x y z A 45 35 20 B 150 50 60 C 125 0 85 D 160 65 0 E 20 120 55	Завдання 5	Завдання 6	Завдання 7
Завдання 8	Завдання 9	Завдання 10	Завдання 11

Завдання 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити.

Завдання 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій.

Завдання 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій.

Завдання 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині  (А, В, С).

Завдання 4. Через пряму АВ провести площину, перпендикулярно до заданої площини  ( CDE). Побудувати лінію перетину двох площин.

Завдання 5. Визначити кут між гранями BEDA та BEFC призми методом заміни площин проекцій.

Завдання 6. Визначити відстань між ребрами AB та SC піраміди методом плоскопаралельного переміщення.

Завдання 7. Визначити натуральну величину кута між прямою l та площиною Р (m || n) методом обертання навколо прямої рівня.

Завдання 8. Побудувати переріз призми площиною загального положення.

Завдання 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу.

Завдання 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях.

Завдання 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.