Умови задач к.1.0.Б - к.1.9.Б (оцінка п’ять балів)

Номер умови	R, cм
0	30
1	40
2	80
3	10
4	40
5	90
6	50
7	70
8	10
9	30

см/c.

3. Аналогічно знайдемо прискорення точки:

При с:

см/c²;

см/c²;

см/c².

4. Дотичне прискорення знайдемо, диференціюючи за часом рівність:

Одержимо:

Тоді:

При с:

см/c².

5. Нормальне прискорення точки:

При с:

см/c².

6. Радіус кривизни траєкторії:

При с:

см.

Відповідь:

см/c; см/c²; см/c²;

см/c²; см.

Побудуємо траєкторію руху точки за знайденим рівнянням еліпса:

Проведемо осі координат ху і виберемо масштаб для побудови еліпса (рис. 27.1). Позначаємо центр еліпса О (2;-1), проводимо допоміжні лінії, паралельні до осей х і у та відкладаємо малі і великі піввісі а = 3 см, b = 5 см у вибраному масштабі. Будуємо еліпс.

Позначимо на траєкторії точки М₀(2; 4) і М₁(-0,6; 1,5).

Далі обираємо масштаби швидкостей і прискорень. Від точки М₁ відкладаємо у вибраному масштабі проекції швидкості (з урахуванням знаків): - ліворуч від точки і - униз від точки. На одержаних векторах будуємо паралелограм швидкостей, діагональ якого є швидкістю . Цей вектор повинен пройти по дотичній до траєкторії. Аналогічно відкладаємо вектори проекцій прискорення, враховуючи знаки: - праворуч

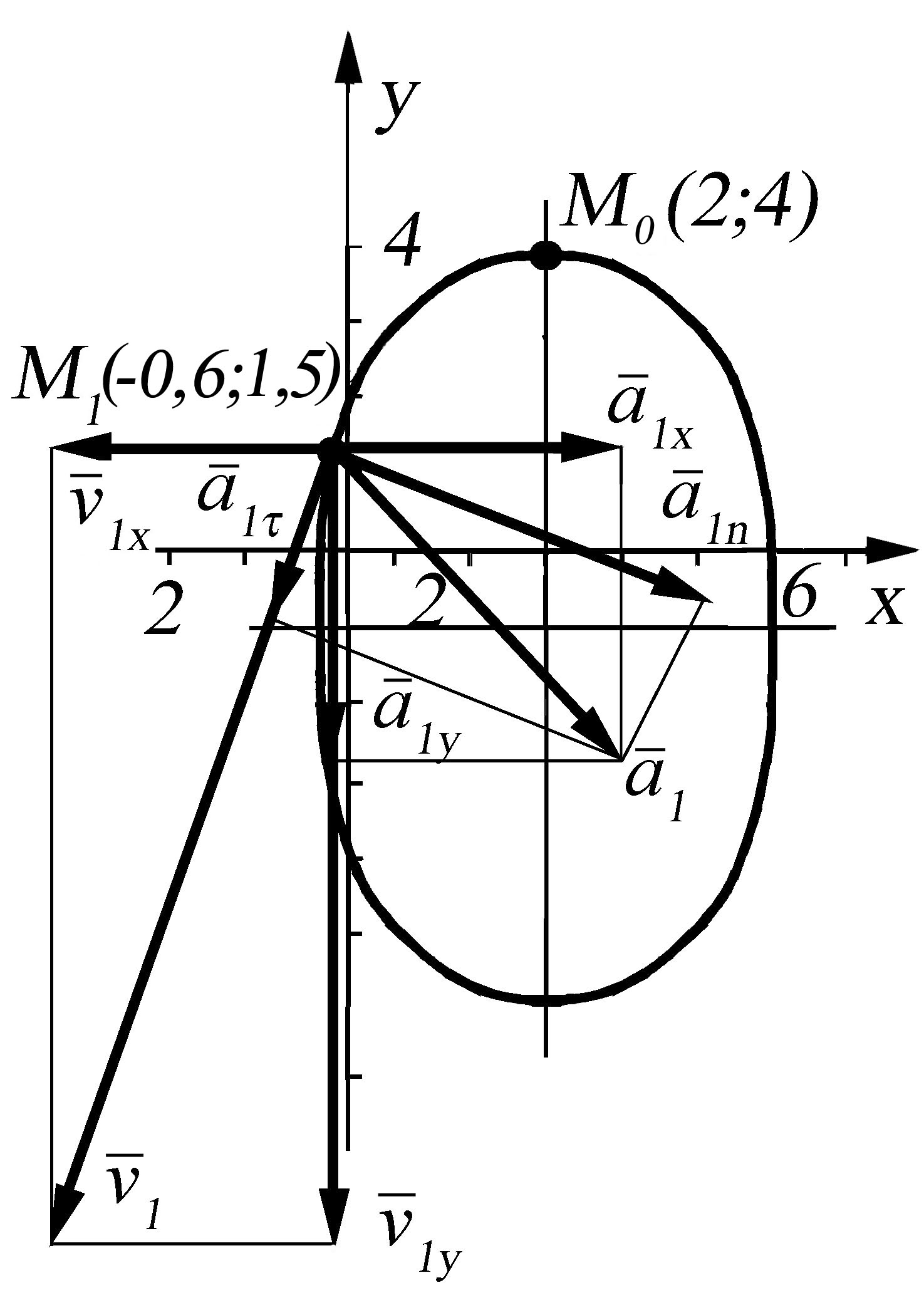
Рис. 27.1

від точки і - униз від точки. Будуємо паралелограм прискорень, діагональ якого є повним прискоренням точки .

Тепер будуємо вектор . Якщо при підрахунках має знак “мінус”, то відкладаємо цей вектор протилежно до вектора швидкості , а якщо знак „плюс” – то по вектору швидкості .

Вектор відкладаємо від точки М₁ у вибраному масштабі перпендикулярно до вектора у бік угнутості кривої (до центра її кривизни).

Якщо розрахунки та побудова виконані вірно, то діагоналлю паралелограма, побудованого на векторах і , буде вектор , одержаний попередньою побудовою.

Приклад розв’язання задачі К.1. Другий рівень складності

Спочатку необхідно розв’язати задачу першого рівня складності.

Тепер розглянемо задачу про рух матеріальної точки В у просторі. Закон руху точки В заданий рівняннями:

,

де х, у, – координати точки, виражені в сантиметрах; t – час у секундах.

Дано:

;

;

с.

Визначити: рівняння траєкторії точки; для моменту часу знайти швидкість і прискорення точки, а також її дотичне, нормальне прискорення та радіус кривизни траєкторії у відповідній точці.

Розв'язання 1. Знайдемо рівняння траєкторії:

Підставимо це значення в рівняння, що виражають координати х і z:

Як відомо з аналітичної геометрії, у просторі лінії відповідають два рівняння з трьома координатами. Таким чином, рівняння траєкторії точки в координатній формі будуть такими:

2. Знайдемо швидкість точки:

При с:

см/c; см/c; см/c;

см/c.

2. Аналогічно знайдемо прискорення точки:

При с:

см/c²;

см/c²;

см/c².

2. Дотичне прискорення точки:

При с:

см/c².

2. Нормальне прискорення точки:

При с:

см/c².

2. Радіус кривизни траєкторії:

При с:

см.

Відповідь:

см/c; см/c²; см/c²;

см/c²; см.

Приклад розв’язання задачі К.1. Третій рівень складності

Спочатку необхідно розв’язати дві задачі: першого та другого рівнів складності.

Розглянемо додаткову задачу про рух матеріальної точки по колу радіуса R за законом (тут S – криволінійна координата точки, виражена в сантиметрах; t – час у секундах).

Дано: см; см; с.

Знайти: швидкість, прискорення, тангенціальне та нормальне прискорення точки.

Розв'язання 1. Визначимо швидкість точки:

.

При с:

см/с.

2. Визначимо тангенціальне прискорення точки:

.

При с:

см/с².

3. Визначимо нормальне прискорення точки:

.

При с:

см/с².

4. Визначимо повне прискорення точки:

.

При с:

см/с².

Відповідь:

см/с; см/с²; см/с²; см/с².

229