
Модуль моменту сили
![]() ,
(5)
,
(5)
де
![]() —
кут між
—
кут між
![]() і
і
![]() ;
;
![]() — плече сили
— довжина перпендикуляра, опущеного з
точки О
на лінію дії сили
— плече сили
— довжина перпендикуляра, опущеного з
точки О
на лінію дії сили
![]() .
.
Момент сили відносно
нерухомої вісі
Z,
яка співпадає
з напрямком вектора
![]() ,
то момент сили зображається у вигляді
вектора, який співпадає з віссю:
,
то момент сили зображається у вигляді
вектора, який співпадає з віссю:
![]() .
(6)
.
(6)
Для нашого випадку плече сили дорівнює радіусу обода колеса R, тоді модуль моменту сили дорівнює
![]() . (7)
. (7)
З рівнянь (2) та (7) отримаємо кутове прискорення колеса:
![]() . (8)
. (8)
Для однорідного
диска (циліндра) радіуса
![]() і масою
і масою
![]() відносно осі, що збігається з віссю
диска, момент інерції дорівнює:
відносно осі, що збігається з віссю
диска, момент інерції дорівнює:
![]() ; (9)
; (9)
Момент інерції з виразу (9) підставляємо в вираз (8) і отримаємо вираз для розрахунку кутового прискорення:
![]() = (10)
= (10)
З рівняння кутової
швидкості визначаємо час
t,
після
початку
дії сили, коли колесо буде мати частоту
обертання
![]() :
:
![]() ,
при умові, що
,
при умові, що
![]() = 0. (11)
= 0. (11)
Дані умови задачі підставляємо в вирази (10) та (11) і отримаємо відповіді:
![]() =
=
![]() =
=
-
До краю стола прикріплений блок (див. рис. 1.78). Через блок перекинена невагома нитка, до кінців якої прикріплені вантажі. Один вантаж рухається по поверхні стола, а інший - вздовж вертикалі вниз. Визначити коефіцієнт тертя між поверхнею вантажу і столу, якщо маса кожного вантажу і маса блоку однакові і вантажі рухаються з прискоренням а = 5,6 м/с2. Силою тертя на блоці нехтувати.
1.78.
Рис. 1.78.
Дано
m1
= m2
=
а
= 5,6 м/с2

![]() =
=
![]()
![]() = ?
= ?
Запишемо основне рівняння динаміки руху усіх зв’язаних тіл:
 . (1)
. (1)
Момент сили знаходимо за формулою:
![]() , (2)
, (2)
де
![]() - радіус блоку.
- радіус блоку.
Момент інерції блоку визначаємо за формулою для диску, ось обертання якого проходить через його центр мас:
![]() , (3)
, (3)
а кутове прискорення можна визначити за формулою:
![]() . (4)
. (4)
З перших двох рівнянь системи (1) визначаємо сили натягу нитки і підставляємо в рівняння (2), в якому розписуємо момент сили:
![]() , (5)
, (5)
З останнього рівняння (5) визначаємо коефіцієнт тертя між поверхнею вантажу і столу:
![]() = (6)
= (6)
Дані умови задачі підставляємо в вираз (6) і отримаємо відповідь:
![]() =
=
-
Кулька масою m = 60 г, що прив'язана до кінця нитки довжиною L1 = 1,2 м, обертається з частотою
 =
2 с-1,
опираючись на горизонтальну площину.
Нитка скорочується, наближаючи кульку
до осі на відстань L2
= 0,6 м.
З якою частотою
=
2 с-1,
опираючись на горизонтальну площину.
Нитка скорочується, наближаючи кульку
до осі на відстань L2
= 0,6 м.
З якою частотою
 ,
буде при
цьому обертатися кулька? Яку роботу
здійснює
зовнішня сила, укорочуючи нитку?
,
буде при
цьому обертатися кулька? Яку роботу
здійснює
зовнішня сила, укорочуючи нитку?
1.79.
Дано
m
= 60 г L1
= 1,2 м L2
= 0,6 м
![]() =
2 с-1
=
2 с-1
![]() = ?
= ?
![]() = ?
= ?
Закон збереження моменту імпульсу в ізольованій механічній системі, якою можна вважати кульку, що рухається без тертя о горизонтальну поверхню, на яку вона опирається, має вигляд:
![]() , (1)
, (1)
де момент інерції
кульки визначаємо як для матеріальної
точки, тобто
![]() .
.
З рівняння (1) знаходимо вираз для розрахунку другої частоти:
![]() = (2)
= (2)
Роботу, яку здійснює зовнішня сила, укорочуючи нитку, визначаємо з зміни кінетичної енергії кульки:
![]() . (3)
. (3)
Дані умови задачі (виражені в одиницях системи СІ) підставляємо в вирази (2) та (3) і отримаємо відповіді:
![]() =
= ![]() =
=
-
Маховик, момент інерції якого J = 63,6 кгм2, обертається з кутовою швидкістю = 31,4 рад/с. Найти момент сил гальмування М, під дією якого маховик зупиняється через час t = 20 с. Маховик вважати однорідним диском.
1.80.
Дано
J
= 63,6 кгм2 0
= 31,4 рад/с t
= 20 с
![]() = ?
= ?
Основне рівняння динаміки обертального руху твердого тіла має вигляд:
![]() , (1)
, (1)
де
![]() — геометрична
сума моментів зовнішніх сил;
— геометрична
сума моментів зовнішніх сил;
![]() — момент інерції тіла;
— момент інерції тіла;
![]() — кутове
прискорення.
— кутове
прискорення.
Або в скалярному вигляді маємо
![]() , (2)
, (2)
де кутове прискорення дорівнює:
![]() . (3)
. (3)
Підставляємо прискорення з рівняння (3) у формулу (2) і визначаємо момент сил гальмування:
![]() =
=
-
Маховик радіусом R = 0,2 м і масою m = 10 кг зчеплений з мотором за допомогою привідного ременя. Сила натягу ременя, що йде без ковзання, Т = 14,7 Н. Яку частоту обертання буде мати маховик через час t = 10 с після початку руху? Маховик вважати однорідним диском. Тертям знехтувати.
1.81.
Дано
R
= 0,2 м m
= 10 кг Т
= 14,7 Н t
= 10 с
![]() = ?
= ?
Основне рівняння динаміки обертального руху твердого тіла має вигляд:
![]() , (1)
, (1)
де
![]() — геометрична
сума моментів зовнішніх сил;
— геометрична
сума моментів зовнішніх сил;
![]() — момент інерції тіла;
— момент інерції тіла;
![]() — кутове
прискорення.
— кутове
прискорення.
Або в скалярному вигляді для нашого випадку маємо
![]() , (2)
, (2)
де момент інерції однорідного диску дорівнює
![]() , (3)
, (3)
а прискорення дорівнює:
![]() . (4)
. (4)
Звідки отримаємо частоту обертання, яку буде мати маховик через час t після початку руху:
![]() . (5)
. (5)
Підставляємо прискорення з рівняння (2) та момент інерції з формули (3) у формулу (5) і отримуємо вираз для розрахунку частоти:
![]() = (6)
= (6)
Дані умови задачі підставляємо в вираз (6) і отримаємо відповідь:
![]() =
=
-
По дотичній до шківа маховика у вигляді диска діаметром D = 75 см і масою m = 40 кг прикладена сила F = 1 кН. Визначити кутове прискорення
 і частоту обертання
і частоту обертання
 маховика через час t
= 10 с після
початку
дії сили, якщо
радіус шківа r
= 12 см.
маховика через час t
= 10 с після
початку
дії сили, якщо
радіус шківа r
= 12 см.
1.82.
Дано
D
= 75 см m
= 40 кг t
= 10 с
![]() =
1 кН
=
1 кН![]() = 12 см
= 12 см
![]() = ?
= ?
![]() = ?
= ?
О
Рис. 1.82
![]() , (1)
, (1)
де
![]() — геометрична
сума моментів зовнішніх сил;
— геометрична
сума моментів зовнішніх сил;
![]() — момент інерції тіла;
— момент інерції тіла;
![]() — кутове
прискорення.
— кутове
прискорення.
Або в скалярному вигляді для нашого випадку маємо
![]() ,
(2)
,
(2)
де момент інерції однорідного диску дорівнює (момент інерції шківа не враховуємо бо незадана його маса):
![]() , (3)
, (3)
Робимо підстановку моменту інерції з виразу (3) у вираз (2) для отримання формули для розрахунку кутового прискорення:
![]() = (4)
= (4)
З
відомої формули прискорення визначаємо
частоту
обертання
![]() маховика через час t
після
початку
дії сили:
маховика через час t
після
початку
дії сили:
![]() . (5)
. (5)
Дані умови задачі підставляємо в вирази (4) та (5) і отримаємо відповіді:
![]() =
=
![]() =
=
-
Н
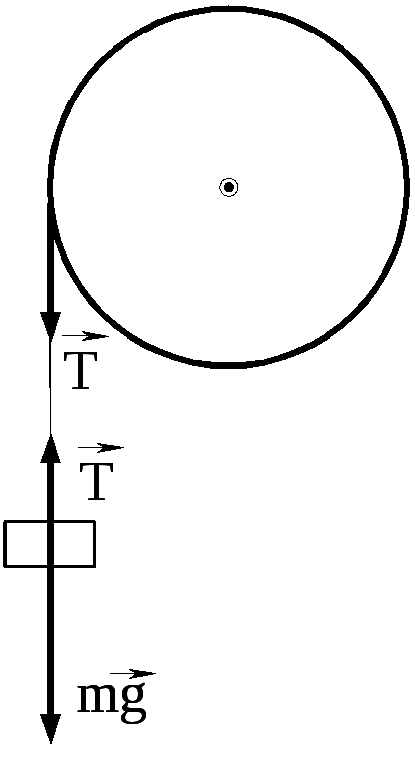
Рис. 1.83
а обід маховика діаметром D = 60 см намотаний шнур, до кінця якого прив'язаний вантаж масою m = 2 кг. Визначити момент інерції J маховика, якщо він обертаючись рівноприскорено під дією сили ваги вантажу, за час t = 3 с придбав кутову швидкість = 9 рад/с.
1.83.
Дано
D
= 60 см m
= 2 кг t
= 3 с
=
9 рад/с
![]() = ?
= ?
Основне рівняння динаміки обертального руху твердого тіла має вигляд:
![]() , (1)
, (1)
де
![]() - геометрична
сума моментів зовнішніх сил;
- геометрична
сума моментів зовнішніх сил;
![]() - момент інерції тіла;
- момент інерції тіла;
![]() - кутове
прискорення.
- кутове
прискорення.
Або в скалярному вигляді для нашого випадку маємо
![]() ,
(2)
,
(2)
Силу натягу шнура визначимо з рівняння руху вантажу:
![]() . (3)
. (3)
З відомої формули визначаємо кутове прискорення:
![]() . (4)
. (4)
Силу натягу шнура з формули (3), кутове прискорення з формули (4) підставляємо у формулу (2) і отримаємо момент інерції J маховика:
![]() = (5)
= (5)
Дані умови задачі підставляємо в вираз (5) і отримаємо відповіді:
![]() =
=
-
Нитка з прив'язаними до її кінців вантажами масами m1 = 50 г та m2 = 60 г перекинута через блок діаметром D = 4 см. Визначити момент інерції J блока, якщо під дією сили ваги вантажів він отримав кутове прискорення = 9 рад/с2. Тертям нитки по блоку знехтувати.
1.84.
Дано
m1
=
50 г m2
=
60 г D
= 4 см
=
9 рад/с2
![]() = ?
= ?
Запишемо основне рівняння динаміки руху усіх зв’язаних тіл:
 . (1)
. (1)
Момент сили знаходимо за формулою:
Рис. 1.84![]()

де
![]() - радіус блоку.
- радіус блоку.
Кутове прискорення блоку пов’язане з лінійним прискоренням точок його ободу формулою:
![]() . (3)
. (3)
З перших двох рівнянь системи (1) визначаємо сили натягу нитки і підставляємо в рівняння (2), в якому розписуємо момент сили:
![]() , (4)
, (4)
З останнього рівняння (4) визначаємо момент інерції J блока:
![]() = (6)
= (6)
Дані умови задачі підставляємо в вираз (6) і отримаємо відповідь:
![]() =
=
-
Стержень обертається навколо осі, що проходить через його середину, у відповідності з рівнянням = A t+B t3, де А = 2 рад/с, В = 0,2 рад/с3. Визначити момент сил, що буде діяти на стержень через t = 2 с після початку його руху. Момент інерції стержня J = 0,048 кг м2.
1.85.
Дано
t
= 2 с J
= 0,048 кг м2
![]() рад
рад
![]() = ?
= ?
Основне рівняння динаміки обертального руху твердого тіла має вигляд:
![]() , (1)
, (1)
де
![]() - геометрична
сума моментів зовнішніх сил;
- геометрична
сума моментів зовнішніх сил;
![]() - момент інерції тіла;
- момент інерції тіла;
![]() - кутове
прискорення.
- кутове
прискорення.
Або в скалярному вигляді для нашого випадку маємо
![]() ,
(2)
,
(2)
Кутове прискорення визначаємо як другу похідну від кута повороту стержня по часу:
![]() . (3)
. (3)
Підставляємо кутове прискорення з виразу (3) та дані умови задачі в вираз (2) і отримаємо відповіді:
![]() =
=
-
Визначити момент сили М, який необхідно прикласти до блока, що обертається з частотою
 = 12 с-1,
щоб він зупинився протягом часу t
= 8 с. Діаметр блоку D
= 30 см. Масу блоку m
= 6 кг
вважати
рівномірно розподіленою по ободу.
= 12 с-1,
щоб він зупинився протягом часу t
= 8 с. Діаметр блоку D
= 30 см. Масу блоку m
= 6 кг
вважати
рівномірно розподіленою по ободу.
1.85.
Дано
t
= 8 с D
= 30 см m
= 6 кг
![]() =
12 с-1
=
12 с-1
![]() = ?
= ?
Основне рівняння динаміки обертального руху твердого тіла має вигляд:
![]() , (1)
, (1)
де
![]() - геометрична
сума моментів зовнішніх сил;
- геометрична
сума моментів зовнішніх сил;
![]() - момент інерції тіла;
- момент інерції тіла;
![]() - кутове
прискорення.
- кутове
прискорення.
Або в скалярному вигляді для нашого випадку маємо
![]() ,
(2)
,
(2)
Середнє кутове прискорення визначаємо за формулою:
![]() (3)
(3)
оскільки блок зупинився.
Момент інерції блоку, маса якого рівномірно розподіленою по ободу, а вісь обертання проходить через його центр, дорівнює
![]() . (4)
. (4)
Підставляємо кутове прискорення з виразу (3), момент інерції з виразу (4) та дані умови задачі в вираз (2) і отримаємо відповіді:
![]() =
=
-
Циліндр, розташований горизонтально, може обертатися навколо осі, що співпадає з віссю циліндра. Маса циліндра
 = 12
кг. На циліндр намотали шнур, до якого
прив'язали гирю масою m2
= 1 кг. З яким прискоренням буде опускатися
гиря? Яка сила натягу шнура під час
руху гирі?
= 12
кг. На циліндр намотали шнур, до якого
прив'язали гирю масою m2
= 1 кг. З яким прискоренням буде опускатися
гиря? Яка сила натягу шнура під час
руху гирі?
Рис. 1.87
1.87.
Дано
m2
= 1 кг
![]() = 12
кг
= 12
кг
![]() = ?
= ?
![]() = ?
= ?
Основне рівняння динаміки обертального руху твердого тіла має вигляд:
![]() , (1)
, (1)
де
![]() - геометрична
сума моментів зовнішніх сил;
- геометрична
сума моментів зовнішніх сил;
![]() - момент інерції тіла;
- момент інерції тіла;
![]() - кутове
прискорення.
- кутове
прискорення.
Або в скалярному вигляді для нашого випадку маємо
![]() ,
(2)
,
(2)
де момент інерції циліндра навколо осі, що співпадає з віссю циліндра дорівнює
![]() , (3)
, (3)
Тоді
сила натягу шнура визначається з формули
(2) с використанням формули (3) та зв’язку
між кутовим та лінійним прискоренням
(![]() ):
):
![]() ,
(4)
,
(4)
З рівняння динаміки руху вантажу отримаємо силу натягу шнура:
![]() . (5)
. (5)
Порівнюючи праві частини рівнянь (4) і (5) отримаємо рівняння для розрахунку прискорення:
![]() . (6)
. (6)
Прискорення з виразу (5) підставляємо у формулу (4) і отримаємо вираз для розрахунку сила натягу шнура під час руху гирі:
![]() = (7)
= (7)
Дані умови задачі підставляємо в вирази (6) та (7) і отримаємо відповіді:
![]() =
=
![]() =
=
-
Через блок масою M = 200 г, виконаний у вигляді колеса, перекинена нитка, до кінців якої прив'язані вантажі масами m1 = 100 г і m2 = 300 г. Визначити прискорення, з яким будуть рухатися вантажі, і сили натягу нитки по обидві сторони блока.
1.88.
Дано
M
= 200 г m1
=
100 г m2
=
300 г
![]() = ?
= ?
![]() = ?
= ?
Запишемо основне рівняння динаміки руху усіх зв’язаних тіл:
Рис. 1.88
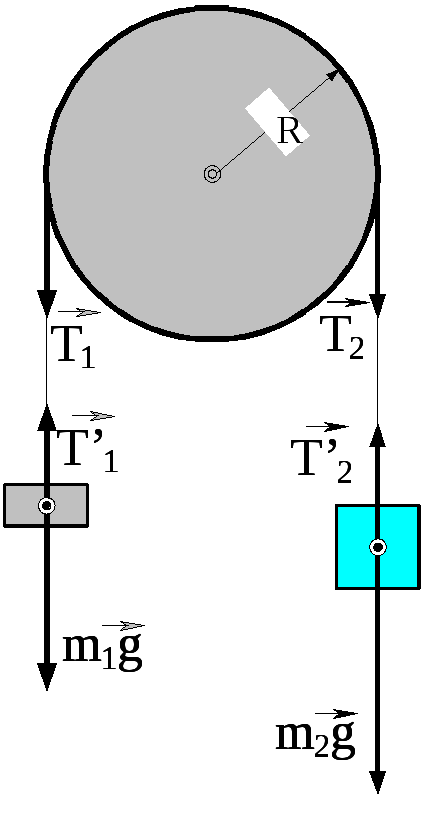
Момент сили знаходимо за формулою:
![]() , (2)
, (2)
де
![]() - радіус блоку.
- радіус блоку.
Кутове прискорення блоку пов’язане з лінійним прискоренням точок його ободу формулою:
![]() . (3)
. (3)
З перших двох рівнянь системи (1) визначаємо сили натягу нитки і підставляємо в рівняння (2), в якому розписуємо момент сили:
![]() , (4)
, (4)
З останнього рівняння (4) визначаємо момент інерції J блока:
![]() = (6)
= (6)
Дані умови задачі підставляємо в вираз (6) і отримаємо відповідь:
![]() =
=
-
Двом однаковим маховикам, що знаходяться в спокої, надали однакову кутову швидкість = 63 рад/с і надали їх самим собі. Під дією сил тертя перший маховик зупинився через одну хвилину, а другий зробив до повної зупинки N = 360 обертів. У скільки разів момент сил тертя у першого маховика був більшим ніж у другого?
1.89.
Дано
=
63 рад/с N
= 360 обертів
![]() = 1 хв
= 1 хв
![]() = ?
= ?
Основне рівняння динаміки обертального руху твердого тіла має вигляд:
![]() , (1)
, (1)
де
![]() - геометрична
сума моментів зовнішніх сил;
- геометрична
сума моментів зовнішніх сил;
![]() - момент інерції тіла;
- момент інерції тіла;
![]() - кутове
прискорення.
- кутове
прискорення.
Або в скалярному вигляді для нашого випадку маємо
![]() ,
(2)
,
(2)
Запишемо відношення моментів сил тертя
![]() . (3)
. (3)
Кутове прискорення першого маховика визначимо як середнє:
![]() . (4)
. (4)
Кутове прискорення другого маховика визначимо з кількості обертів, які він зробив до повної зупинки:
 . (5)
. (5)
Підставляємо кутові прискорення з виразів (4) та (5) у формулу (3) і отримаємо вираз для розрахунку:
![]() = (6)
= (6)
Дані умови задачі підставляємо в вираз (6) і отримаємо відповідь:
![]() =
=
-
Куля скочується з похилої площини висотою h = 90 см. Яку лінійну швидкість буде мати центр кулі у момент, коли вона скотиться з похилої площини?
1.90.
Дано
h
= 90 см
![]() = ?
= ?
Згідно з законом збереження механічної енергії для замкненої системи тіл, потенціальна енергія кулі переходить в її кінетичну енергію поступального та обертального руху:
![]() , (1)
, (1)
де
![]() - маса кулі;
- маса кулі;
![]() ,
,
![]() - лінійна і кутова швидкість кулі, які
пов’язані між собою рівнянням
- лінійна і кутова швидкість кулі, які
пов’язані між собою рівнянням
![]() ;
;
![]() - момент інерції кулі відносно її центру
мас.
- момент інерції кулі відносно її центру
мас.
Змінимо рівняння (1) з урахуванням наведених зв’язків:
![]() , (2)
, (2)
звідки отримаємо вираз для розрахунку швидкості:
![]() = (3)
= (3)
Дані умови задачі (виражені в системі одиниць СІ) підставляємо в вираз (3) і отримаємо відповідь:
![]() =
=
-
На верхній поверхні горизонтального диска, який може обертатися навколо вертикальної осі, прокладені по колу радіусом r1 =50 см рейки іграшкової залізниці. Маса диска
 = 10 кг, а його радіус R2
= 60 см. На рейки нерухомого диска був
поставлений заводний паровозик масою
= 10 кг, а його радіус R2
= 60 см. На рейки нерухомого диска був
поставлений заводний паровозик масою
 =
1 кг. Він почав рухатися відносно рейок
з швидкістю
=
1 кг. Він почав рухатися відносно рейок
з швидкістю
 =
0,8 м/с. З якою кутовою швидкістю буде
обертатися диск?
=
0,8 м/с. З якою кутовою швидкістю буде
обертатися диск?
1.91.
Дано
r1
=50 см R2
= 60 см
![]() =
10 кг
=
10 кг![]() =
1 кг
=
1 кг![]() =
0,8 м/с
=
0,8 м/с
![]() = ?
= ?
Закон збереження моменту імпульсу в ізольованій механічній системі має вигляд:
![]() . (1)
. (1)
У скалярному вигляді цей закон можна записати так:
![]() , (2)
, (2)
де
![]() - момент інерції заводного
паровозика, який вважаємо матеріальною
точкою;
- момент інерції заводного
паровозика, який вважаємо матеріальною
точкою;
![]() - його кутова швидкість;
- його кутова швидкість;
![]() - момент інерції лиска з паровозиком;
- момент інерції лиска з паровозиком;
![]() - його кутова швидкість.
- його кутова швидкість.
У рівняння (2) підставляємо приведені значення моментів інерції і кутової швидкості паровозика
![]() . (3)
. (3)
З рівняння (3) отримуємо вираз для розрахунку кутової швидкості з якою буде обертатися диск:
![]() = (4)
= (4)
Дані умови задачі (виражені в системі одиниць СІ) підставляємо в вираз (4) і отримаємо відповідь:
![]() =
=
-
Блок, що має форму диска масою
 =
0,4 кг,
обертається під дією сили натягу нитки,
до кінців якої підвішені вантажі
масами
=
0,4 кг,
обертається під дією сили натягу нитки,
до кінців якої підвішені вантажі
масами
 = 0,3 кг
та
= 0,3 кг
та
 = 0,7 кг.
Визначити сили натягу Т1
і Т2
нитки по обидві сторони
блоку.
= 0,7 кг.
Визначити сили натягу Т1
і Т2
нитки по обидві сторони
блоку.
1.92.
Дано
m1
=
0,3 кг
Рис. 1.92
![]() =
0,4 кг
=
0,4 кг
![]() =
0,7 кг
=
0,7 кг
![]() = ?
= ?
![]() = ?
= ?
Запишемо основне рівняння динаміки руху усіх зв’язаних тіл:
 . (1)
. (1)
Момент сили знаходимо за формулою:
![]() , (2)
, (2)
де
![]() - радіус блоку.
- радіус блоку.
Момент інерції диску відносно осі, яка проходить через його центр мас, визначається за формулою:
![]() . (3)
. (3)
Кутове прискорення блоку пов’язане з лінійним прискоренням точок його ободу формулою:
![]() . (4)
. (4)
З перших двох рівнянь системи (1) визначаємо сили натягу нитки:
![]() , (5)
, (5)
та
![]() , (6)
, (6)
і підставляємо в рівняння (2), в якому розписуємо момент сили згідно з виразом (3):
![]() , (7)
, (7)
З останнього рівняння (7) визначаємо прискорення грузів:
![]() . (8)
. (8)
Значення прискорення з виразу (8) підставляємо в вираз (5) та (6) і отримаємо вирази для розрахунку сили натягу Т1 і Т2 нитки по обидві сторони блоку:
![]() = (9)
= (9)
та
![]() = (10)
= (10)
Дані умови задачі підставляємо в вирази (9) та (10) і отримаємо відповіді:
![]() =
=
![]() =
=
-
Куля масою m = 1 кг, що котиться без ковзання, ударяється об стінку і відкочується від неї. Швидкість кулі до удару об стінку
 = 10 см/с,
після
удару -
= 10 см/с,
після
удару -
 = 8 см/с.
Найти кількість теплоти Q,
що виділилася при
ударі кулі об стіну.
= 8 см/с.
Найти кількість теплоти Q,
що виділилася при
ударі кулі об стіну.
1.93.
Дано
m
= 1 кг
![]() = 10 см/с
= 10 см/с![]() = 8 см/с
= 8 см/с
![]() = ?
= ?
Для спрощення розв’язку задачі, вважаємо що рух кулі відбувається у горизонтальному напрямку, тоді кількість теплоти Q, яка може виділитись при ударі кулі об стінку, дорівнюватиме зміні кінетичної енергії кулі:
![]() . (1)
. (1)
Кінетична енергія
кулі як до удару
![]() ,
так і після нього
,
так і після нього
![]() ,
складається з кінетичної енергії
поступального і обертального руху:
,
складається з кінетичної енергії
поступального і обертального руху:
 (2)
(2)
Оскільки куля котиться без ковзання, то між кутовою швидкістю її обертання та лінійною швидкістю руху центру мас кулі існує такий зв'язок:
![]() , (3)
, (3)
а момент інерції кулі відносно вісі, що проходить через його центр мас, визначається формулою:
![]() , (4)
, (4)
тоді систему рівнянь (2) можна записати так:
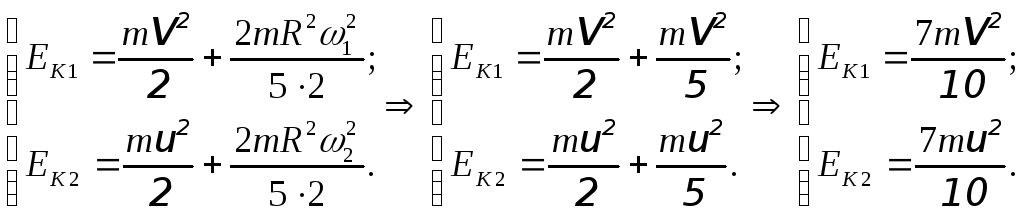 (5)
(5)
Отримані в (5) вирази для кінетичної енергії кулі до і після удару підставляємо у формулу (1) і отримаємо вираз для розрахунку кількість теплоти Q, що виділилася при ударі кулі об стіну:
![]() = (6)
= (6)
Дані умови задачі (виражені в системі одиниць СІ) підставляємо в вираз (6) і отримаємо відповідь:
![]() =
=
-
Диск діаметром D = 60 см і масою m = 1 кг обертається навколо осі, що проходить через його центр з частотою
 = 20 об/с. Яку роботу
А
треба здійснити, щоб зупинити
диск?
= 20 об/с. Яку роботу
А
треба здійснити, щоб зупинити
диск?
1.94.
Дано
D
= 60 см m
= 1 кг
![]() =
20
об/с
=
20
об/с
![]() = ?
= ?
Робота, яку треба здійснити, щоб зупинити диск дорівнюватиме зміні кінетичної енергії диску:
![]() , (1)
, (1)
а кінетична енергія обертового руху визначається за формулою:
![]() , (2)
, (2)
де момент інерції диску відносно осі, що проходить через його центр, дорівнює
![]() , (3)
, (3)
якщо диск зупиниться, то його кінетична енергія дорівнюватиме нулю, тоді вираз (1) матиме вигляд:
![]() , (4)
, (4)
де кутову швидкість визначають через частоту обертання диску:
![]() . (5)
. (5)
Вираз кутової швидкості з (5) підставляємо в формулу (4) і отримаємо вираз для розрахунку роботи:
![]() = (6)
= (6)
Дані умови задачі (виражені в системі одиниць СІ) підставляємо в вираз (6) і отримаємо відповідь:
![]() = =
= =
-
До кінців легкої і нерозтяжної нитки, перекиненої через блок, підвішені вантажі масою m1 = 0,2 кг і m2 = 0,3 кг. У скільки разів відрізняються сили, діючі на нитку по обидві сторони від блоку, якщо маса блоку m = 0,4 кг, а його вісь рухається вертикально вгору з прискоренням а = 2 м/с2 ? Силами тертя знехтувати.
1.95.
Дано
m1
=
0,2 кг
Рис. 1.95
![]() =
0,4 кг
=
0,4 кг
![]() =
0,3 кг
=
0,3 кг
![]() = ?
= ?
![]() = ?
= ?
Запишемо основне рівняння динаміки руху першого та другого тіл:
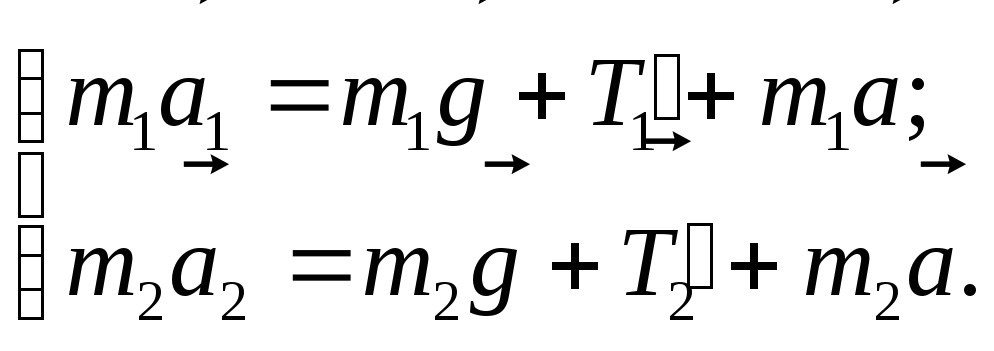 . (1)
. (1)
У скалярному вигляді в проекціях на напрям руху (вгору) ця система матиме вигляд:
 . (2)
. (2)
Звідки можна отримати сили натягу:
 . (3)
. (3)
Оскільки вантажі зв’язані, то їхні прискорення однакові, тому позначимо їх однією буквою:
![]() , (4)
, (4)
і отримаємо нову систему рівнянь (3):
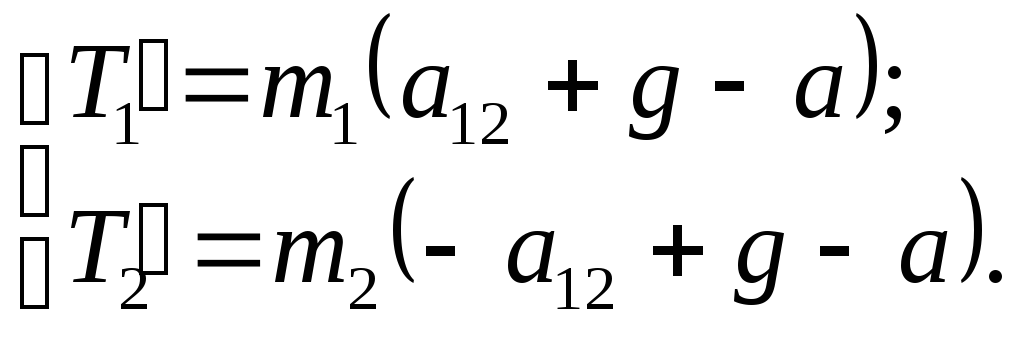 . (5)
. (5)
Запишемо основне рівняння динаміки обертального руху для блоку:
![]() , (6)
, (6)
Враховуючи,
що
![]() ,
,
![]() ,
,
![]() - момент інерції шківа (диску), а
- момент інерції шківа (диску), а
![]() для точок ободу шківа, та вирази з системи
(5), отримаємо з виразу (6) таке рівняння
для точок ободу шківа, та вирази з системи
(5), отримаємо з виразу (6) таке рівняння
![]() ,
(7)
,
(7)
звідки визначаємо прискорення вантажів:
 . (8)
. (8)
Дані умови задачі підставляємо в вираз (8), а отримане прискорення підставляємо у формули (5) і отримаємо відповіді:
![]() =
=
![]() =
=
-
Платформа у вигляді диска діаметром D = 3 м і масою m1 = 180 кг може обертатися навколо вертикальної осі. З якою кутовою швидкістю 1 буде обертатися ця платформа, якщо по її краю піде людина масою m2 = 70 кг з швидкістю
 =
1,8 м/с
відносно платформи?
=
1,8 м/с
відносно платформи?
1.96.
Дано
D
=
3 м
![]() =
70 кг
=
70 кг![]() =
180 кг
=
180 кг![]() =
1,8 м/с
=
1,8 м/с
![]() = ?
= ?
Для розв’язку задачі використаємо закон збереження моменту імпульсу в ізольованій механічній системі, який має вигляд:
![]() . (1)
. (1)
Для системи з двох тіл цей закон можна записати у вигляді:
![]() , (2)
, (2)
де
![]() - момент інерції людини,
яку вважаємо матеріальною точкою;
- момент інерції людини,
яку вважаємо матеріальною точкою;
![]() - його кутова швидкість;
- його кутова швидкість;
![]() - момент інерції диска і людини;
- момент інерції диска і людини;
![]() - його кутова швидкість.
- його кутова швидкість.
У рівняння (2) підставляємо приведені значення моментів інерції і кутової швидкості людини
![]() . (3)
. (3)
З рівняння (3) отримуємо вираз для розрахунку кутової швидкості з якою буде обертатися диск:
![]() = (4)
= (4)
Дані умови задачі (виражені в системі одиниць СІ) підставляємо в вираз (4) і отримаємо відповідь:
![]() =
=
-
Платформа, що має форму диска, може обертатися навколо вертикальної осі. На краю платформи стоїть людина. На який кут повернеться платформа, якщо людина піде вздовж краю платформи і, обійшовши її, повернеться в початкову точку? Маса платформи m1 = 280 кг, маса людини m2 = 80 кг.
1.97.
Дано
![]() =
280 кг
=
280 кг![]() =
80 кг
=
80 кг
![]() = ?
= ?
Кут, на який повернеться платформа, якщо людина піде вздовж краю платформи і, обійшовши її, повернеться в початкову точку, можна визначити за кутовою швидкістю обертового руху платформи і часу, за який людина пройде весь шлях, тобто довжину кола з радіусом диску:
![]() . (1)
. (1)
Для визначення кутової швидкості використаємо закон збереження моменту імпульсу в ізольованій механічній системі, який має вигляд:
![]() . (2)
. (2)
Для системи з двох тіл цей закон можна записати у вигляді:
![]() , (3)
, (3)
де
![]() - момент інерції людини,
яку вважаємо матеріальною точкою;
- момент інерції людини,
яку вважаємо матеріальною точкою;
![]() - його кутова швидкість;
- його кутова швидкість;
![]() - момент інерції лиска з людиною;
- момент інерції лиска з людиною;
![]() - його кутова швидкість;
- його кутова швидкість;
![]() - радіус диска.
- радіус диска.
У рівняння (3) підставляємо приведені значення моментів інерції і кутової швидкості людини
![]() . (4)
. (4)
З рівняння (4) отримуємо вираз для розрахунку кута повороту диска:
![]() = (5)
= (5)
Дані умови задачі (виражені в системі одиниць СІ) підставляємо в вираз (5) і отримаємо відповідь:
![]() =
=
-
Однорідний стержень довжиною
 = 1 м
може вільно обертатися навколо
горизонтальної осі, що проходить
через один
з
його кінців. У інший кінець стержня
ударяє куля масою m
= 7 г,
що летіла перпендикулярно стержню і
його осі. Удар кулі був абсолютно
непружним. Визначити масу стержня,
якщо
внаслідок попадання кулі він відхилиться
на кут
= 60°. Швидкість кулі була
= 1 м
може вільно обертатися навколо
горизонтальної осі, що проходить
через один
з
його кінців. У інший кінець стержня
ударяє куля масою m
= 7 г,
що летіла перпендикулярно стержню і
його осі. Удар кулі був абсолютно
непружним. Визначити масу стержня,
якщо
внаслідок попадання кулі він відхилиться
на кут
= 60°. Швидкість кулі була
 =
360 м/с.
=
360 м/с.
1.98.
Дано
m
= 7 г
=
60°
Рис.
1.98
![]() =
1 м
=
1 м![]() =
360 м/с.
=
360 м/с.
![]() = ?
= ?

Зробимо малюнок.
Оскільки
удар
кулі був абсолютно непружним, то куля
і відповідна точка стержня після удару
будуть рухатись з однаковою швидкістю
![]() .
Тобто за малий проміжок часу куля надає
стержню деяку кінетичну енергію:
.
Тобто за малий проміжок часу куля надає
стержню деяку кінетичну енергію:
![]() , (1)
, (1)
де момент інерції стержня відносно осі обертання згідно з формулою Штейнера дорівнює
![]() . (2)
. (2)
Завдяки
цієї енергії, стержень без кулі (за
умовою вона не застрягає в ньому)
повертається на кут
![]() ,
причому його центр тяжіння піднімається
на деяку висоту (див. рис. 1.98):
,
причому його центр тяжіння піднімається
на деяку висоту (див. рис. 1.98):
![]() . (3)
. (3)
При
відхиленні стержень на кут
![]() він буде мати потенціальну енергію, яка
дорівнює
він буде мати потенціальну енергію, яка
дорівнює
![]() . (4)
. (4)
Згідно з законом збереження енергії, можна порівняти праві частини рівнянь (1) та (4) і отримати
![]() . (5)
. (5)
