10.3. Взаємне положення двох прямих.

Паралельність прямих

Дві прямі паралельні, якщо:

1) їх закладання паралельні;

2) інтервали закладання рівні; Рис. 10.7

3) напрями зростання числових позначок однакові.

Приклад. Через т. С15 побудувати СD паралельно до АВ (рис. 10.7).

План розв’язання:

1. виконуємо градуювання АВ та визначаємо інтервал закладання АВ;

2. через точку С15 будуємо закладання СD, паралельно до закладання АВ;

3. на закладанні СD величиною інтервалу закладання АВ виконують градуювання.

Пересічні прямі:

1) у пересічних прямих закладання також пересічні;

2) ЧП точки перетину прямих (т. К) повинна відповідати ЧП інтервалів закладання обох прямих.

Приклад. Побудувати СD, пересічну до АВ (рис. 10.8).

Рис. 10.8 План розв’язання:

1. виконують градуювання АВ;

2. через будь-яку точку інтервалу закладання АВ будують закладання СD, пересічну до АВ і позначають т. К;

3. використовуючи ЧП т. К виконують довільне градуювання СD.

М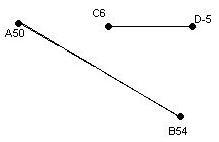имобіжні прямі

Дві прямі є мимобіжними, якщо не виконується хоча б одна з умов паралельності чи пересічності.

Приклад. Побудувати пряму СD, мимобіжну до АВ

Рис. 10.9 (рис. 10.9). СD мимобіжна АВ.

11. Пчп. Площина

11.1. Завдання площини на кресленні.В ПЧП площину задають наступними геометричними елементами:

Рис. 11.1 Рис. 11.2 Рис. 11.3 Рис. 11.4

1) трьома точками (рис. 11.1);

2) прямою і точкою, яка не належить до неї (рис. 11.2);

3) паралельними прямими (рис. 11.3);

4) пересічними прямими (11.4).

Але найбільш поширеним методом завдання площини є завдання за допомогою масштабу закладання площини (рис. 11.5).

Масштаб закладання – це проградуйована проекція лінії найбільшого схилу площини (пряма, перпендикулярна до горизонтальної

Рис. 11.5 площини).

Горизонталь площини – це лінія, яка з’єднує точки з однаковими ЧП.

На кресленні масштаб закладання площини приводять за допомогою тонкої та товстої лінії, на яких нанесене градуювання масштабу закладання. Завжди супроводжується лінійним масштабом.

В ПЧП положення площини у просторі визначають два параметри (рис. 11.6):

1) кут падіння α – це кут нахилу заданої

Рис. 11.6 площини до горизонтальної площини проекції;

Для його визначення необхідно:

- на масштабі закладання площини побудувати дві суміжні горизонталі;

- на першій горизонталі відкласти одиницю лінійного масштабу креслення;

- отриману точку з’єднати з суміжною точкою масштабу закладання площини, що і є рішенням задачі.

2)кут простирання β вимірюється за годинниковою стрілкою від північного напряму вертикальної вісі до правого (позитивного) напряму горизонталі площини.

11.2. Взаємне положення двох площин.

1) Паралельність площин.

Дві площини паралельні, якщо:

1) їх масштаби закладання паралельні;

2) інтервали масштабів закладання рівні;

3) напрями зростання ЧП однакові. Рис. 11.7

Приклад. Побудувати ∆║∑ (рис. 11.7).

1. ∆_і║∑_і.

2. l∆=l_∑.

3. напрями ЧП однакові.

Якщо не виконується хоча б одна з умов паралельності двох площин, вони перетинаються.

Для визначення лінії перетину двох площин Рис. 11.8

необхідно (рис. 11.8):

1) на масштабі закладання площини вибрати по дві точки з однаковими ЧП;

2) через ці точки побудувати по дві горизонталі до їх взаємного перетину;

3) отримані точки з’єднати прямою та проставити їх ЧП.

Приклад. Побудувати лінію перетину двох площин (рис. 11.8).

Г×∆=KL.