Креневич А.П.,Обвінцев О.В.C в задачах і прикладах

3.26. Скласти програми обчислення визначників порядку n:

3.3. Цикли за умовою

На відміну від циклу з лічильником, цикл за умовою виконується не наперед задану кількість разів, а доки істинною є деяка умова. У С є два типи циклів за умовою:

цикл з передумовою while (F) {

Q;

}

цикл з післяумовою do {

Q;

} while (F);

де F – умова, Q – тіло циклу. Обидва цикли виконують набір інструкцій Q, доки умова F залишається істинною. Різниця полягає лише в тому, що для циклу з передумовою перевірка умови F здійснюється до першого виконання тіла циклу Q. Для циклу ж з післяумовою перевірка умови F здійснюється вже після того, як виконається перший раз тіло циклу Q. Цикли з післяумовою здебільшого використовують у випадках, коли умова F є невизначеною до початку виконання циклу.

Зауважимо, що цикл з післяумовою легко отримується з циклу з пе-

До циклів за умовою також належить і цикл з виходом. Окремої конструкції даний тип циклів у С не має. Його моделювання здійснюється за допомогою оператора break. Як тільки програмі трапляється цей оператор, вона припиняє роботу циклу та переходить до виконання наступного оператора, що йде після циклу. Як приклад використання цього оператора наведемо моделювання циклу з виходом з допомогою циклу з передумовою. Нагадаємо, що у С будь-яке ненульове значення арифметичного виразу означає Істину.

Приклади розв'язання задач

Приклад 3.16. Задана непорожня послідовність ненульових цілих чисел, за якою йде 0. Визначити кількість змін знака в цій послідовності. Наприклад, у послідовності 1, −34, 8, 14, −5, 0 знак змінюється тричі.

Розв'язок. Оскільки кількість членів послідовності наперед невідома, то очевидно, що для введення членів послідовності необхідно використати цикл з умовою. Умовою продовження циклу є те, що введене з клавіатури число не є нулем. Тут зручніше використати цикл з післяумовою, оскільки до початку виконання циклу невідомо, яке саме число ввів користувач.

У програмі використаємо допоміжну змінну p, у якій будемо запам'я- товувати попередній член послідовності.

#include <iostream.h> void main(){

int a, p = 0, z = 0; do {

cin >> a;

if (a * p < 0) z++; p = a;

} while (a != 0);

cout << ”кількість знакозмін” << z <<'\n';

}

Наведемо модифікацію попередньої програми з використанням циклу з виходом.

#include <iostream.h> void main(){

int a, p = 0, z = 0; do {

cin >> a;

if (a == 0) break; if (a * p < 0) z++; p = a;

} while (1);

cout << ”кількість знакозмін” << z <<'\n';

}

Приклад 3.17. Послідовність задано рекурентним співвідношенням

x0 = 1, x1 = 0, x2 = 1,

xn = xn−1 + 2xn−2 + xn−3 , n ³ 3.

Створити програму для знаходження номера найменшого члена цієї послідовності, який перевищує число a.

Розв'язок. Оскільки послідовність xn задано рекурентним співвідношенням третього порядку, то для обчислення її довільного елементу

потрібні чотири змінні. Нехай змінна x пробігає послідовність {xn : n ³ 1},

тоді умовою завершення циклу є умова x > а, отже, цикл має виконуватися, доки виконується умова x <= a. Таким чином, маємо програму

#include <iostream.h> void main(){

int n, x, x1, x2, x3, a; cin >> a;

x1 = 1; x2 = 0; x3 = 1; n = 2; do {

n++;

x = x1 + 2*x2 + x3; x3 = x2;

x2 = x1;

x1 = x;

} while (x <= a);

cout << "n = " << n <<'\n';

}

Приклад 3.18. Створити програму для "обернення" (запису в оберненому порядку цифр) заданого натурального числа.

Розв'язок. Нехай у цілочисельній змінній n міститься натуральне число. Скористаємося рекурентним співвідношенням

y0 = 0;

yk = 10 yk −1 + ak ,

де ak – k-та цифра числа n при розгляді цифр справа наліво. Таким чином, програма матиме вигляд:

}

cout << k <<'\n';

}

Приклад 3.19. Маємо ціле n > 2. Знайти всі прості числа з діапазону [2, n]. Розв'язок. Нехай m послідовно набуває значень цілих чисел із діапа-

зону [2, n]. Тоді m буде простим числом, якщо воно не має дільників у діапазоні [2, m ] . Ураховуючи це, напишемо програму:

#include <iostream.h> void main(){

while (n <= 2); // введенню даних. cout << 2 << ", ";

m = 3;

while (m <= n){ p = 1;

k = 3;

while (k * k <= m) { if (m % k == 0) {

p = 0; break;

}

k = k + 2;

}

if (p) cout << m <<", "; m = m + 2;

}

cout << "\n";

}

Приклад 3.20. Написати програму, яка визначає, чи є задане натуральне число n досконалим, тобто рівним сумі всіх своїх дільників, крім самого цього числа (напр., числа 6 і 28: 6 = 1 + 2 + 3, 28 = 1 +2 +4 + 7 + 14).

Розв'язок. Шукатимемо суму S усіх дільників заданого числа n. Якщо S = n, то число, яке перевіряємо, є досконалим. Програму можна написати, використовуючи одну з двох ідей. Перша полягає у знаходженні дільників числа n у діапазоні [1, n/2]. Відповідно до другої ідеї пошук проводиться у діапазоні [1, n ] , і якщо дільник знайдено, то до суми S

додаються як дільник, так і частка.

Напишемо програму згідно з першою ідеєю. У змінній S цілого типу підрахуємо суму дільників, числа, що міститься у змінній n. Використаємо змінну k, яка пробігатиме всі цілі значення в проміжку від 1 до n/2.

if (S == n) cout << "Число є досконалим\n." ; else cout << "Число не є досконалим.\n";

}

Напишемо програму згідно з другою ідеєю. Цього разу змінна k пробігатиме всі цілі значення в проміжку від 1 до sqrt(n). У програмі слід врахувати окремо граничні випадки k = 1 і k=sqrt(n).

}

k = k + 1;

}

if (k * k == n) S += k; // випадок k = sqrt(n) if (S == n) cout << "Число є досконалим\n."; else cout << "Число не є досконалим.\n";

}

Слід зауважити, що програма, написана згідно з першою ідеєю, має коротший та очевидніший запис, проте друга – виконуватиметься значно швидше, оскільки діапазон пошуку дільників суттєво вужчий.

Приклад 3.21. За допомогою розвинення функції у ряд Тейлора обчислити з точністю ε > 0 її значення для заданого значення x.

Зауваження. У загальному випадку обчислення значень алгебраїчних функцій перебуває поза межами даного посібника та вимагає від читача додаткових знань із теорії чисельних методів [9].

Розв'язок. Зафіксуємо параметр х. Розглянемо послідовність

yn = ∑n xk . k =0 k!

Очевидно, що yn → y якщо n → ∞.

Під наближеним із точністю ε значенням границі послідовності yn розумітимемо такий член yN послідовності, що виконується співвідношення

Послідовність yn можна задати рекурентним співвідношенням:

З огляду на рекурентне співвідношення бачимо, що умова (3.6) для yn набуде вигляду |ak| < e. Члени послідовності yn шукатимемо за допомогою циклу за умовою, яка є запереченням умови (3.6). Тоді програма:

#include <iostream.h> #include <math.h> void main(){

}

cout << y << '\n';

}

У вищенаведеній програмі було підключено бібліотеку math.h, де міститься реалізація багатьох математичних функцій. Зокрема, там міститься функція fabs, яка обчислює модуль дійсного числа.

Зауваження. З огляду на попереднє зауваження, слід зазначити, що продемонстрований підхід для інших функцій може призводити до хибних результатів. Тому надалі для таких функцій у формулюванні задачі буде вказано, що потрібно розуміти під наближеним значенням.

Приклад 3.22. Знайти корінь рівняння tgx = x на відрізку [0.001, 1.5] із заданою точністю ε, використовуючи метод ділення відрізка навпіл.

Розв'язок. Метод бісекції (або ділення відрізка навпіл) – один із найпростіших чисельних методів розв'язання нелінійних рівнянь вигляду

f (x) = 0,

де від функції f (x) вимагається лише неперервність. Якщо відомо, що на деякому відрізку існує єдиний корінь цього рівняння, то очевидно, що на кінцях відрізка має бути функція з різними знаками. Поділивши відрізок навпіл, візьмемо ту половину, для якої на кінцях функція набуватиме значень різних знаків. Якщо середина відрізка виявиться нулем функції, то процес завершується. Якщо задано точність обчислення ε, то процедуру поділу слід виконувати, доки довжина відрізка не стане меншою за ε, а наближеним значенням вважають середину цього відрізка.

Отже, для розв'язання рівняння tgx = x розглянемо функцію

}

// корінь – середина останнього відрізка [l,r] x = (l + r) / 2;

cout << x << "\n";

}

Задачі для самостійної роботи

3.30.Для довільного цілого числа m > 1 знайти найбільше ціле k, за якого 4k < m.

3.31.Для заданого натурального числа n одержати найменше число

вигляду 2r, яке перевищує n.

3.32.Визначити, зі скількох від'ємних чисел починається задана послідовність чисел.

3.33.Дано непорожню послідовність різних натуральних чисел, за

якою йде 0. Визначити порядковий номер найменшого з них.

3.34.Дано непорожню послідовність різних дійсних чисел, серед яких

єпринаймні одне від'ємне число, за якою йде 0. Визначити величину найбільшого серед від'ємних членів цієї послідовності.

3.35.Дано непорожню послідовність із натуральних чисел, за

якою йде 0. Обчислити суму тих із них, порядкові номери яких – числа Фібоначчі.

3.36. Маємо дійсне число a. Скласти програму обчислення:

а) серед чисел 1, 1+12, 1+12 +13, ... першого, більшого за a;

б) такого найменшого n, що 1+12 +...+1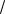n >a. 3.37. Скласти програми обчислення:

а) найбільшого числа Фібоначчі, яке не перевищує число a;