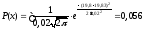1.3 Исследование точности и стабильности технологических процессов обработки

Выполнить исследование точности и стабильности технологического процесса точения Ø20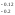детали типа ролик на одношпиндеольном токарно-револьверном автомате.

Для выполнения такого исследования взята выборка последовательно обработанных 58 деталей. По результатам измерений наружного диаметра ролика сформирован интервальный ряд. Этот ряд имеет К=9 интервалов с шагом h=0.01 мм. Значения середин интерваловx- от 19.815 до 19.895 мм. Частоты интервалов (числа деталей, попавших в интервал)nследуют в порядке возрастания номера интервала 2,2,5,9,14,13,8,4,1 . Значения середин интервалов х заданы дискретным аргументом от 19.815 с шагом 0.01, а также приведены частотыn, расчет среднего арифметическогоx, и среднего квадратичного отклоненияS.

Выявляем наибольшее и наименьшее значение выборки: х_min,x_max

x_max= 23; х_min =1

Определяем размах варьирования выборки:

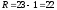
N>50 обработку эмпирических данных рекомендуется вести по значениям, сгруппированным вКнепересекающихся интервалов.

Определяем приближенное количество интервалов группирования:

К = 1+ 3,3lgN

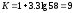
Определяем величину интервала группирования ∆х:

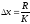
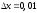
После этого строим гистограмму частот nи по виду ее делается вывод о предполагаемом теоретическом распределении, хорошо описывающем наблюдаемое, т.е. статистическое.

Рисунок 1.1 − Гистограмма частот

Основные этапы исследования следующие:

- формируем интервальный ряд (х_i;n_i),

где х_i;n_iсоответственно значение размераi-той детали и частость;

- Вычисляем основные характеристики: х_а – математическое ожидание (среднее арифметическое) иS– выборное среднеквадратическое отклонение;

,

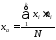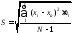
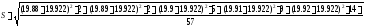
- вычисляем теоретические (выравнивающие) частоты nt_i в предположении нормального закона распределения

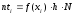
где 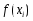- функция плотности распределения случайной величины (размера);

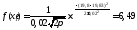
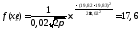
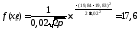
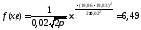
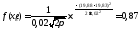
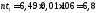
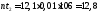
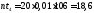
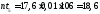
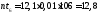
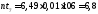
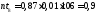
- сравниваем визуально эмпирические 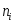и теоретические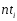частоты построением гистограммы частот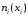ина одном графике;

- производим проверку нулевой гипотезы, т.е. гипотезы о соответствии предполагаемого нормального распределения наблюдаемому по критериям Колмогорова и Пирсона

Критерий Колмогорова вычисляем следующим образом:

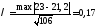
Расчетное значение критерия Колмогорова 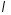сравниваем с, взятым из таблиц квантилей распределения Колмогорова (Приложение 1), гдеР – уровень значимости, который рекомендуется в пределахР= 0,2…0,3. Если<, то нулевая гипотеза принимается.

Расчетное значение критерия Пирсона:

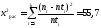
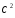сравниваем с квантилями распределения Пирсона (Приложение 2), которые определяются в зависимости от Р – уровня значимости и числа степеней свободыf=K-3.Если<, то нулевая гипотеза принимается.

После этого проводится сравнение результатов наблюдения с требованиями чертежа. Допуск на размер по чертежу и достоверный диапазон рассеивания наблюдаемого размера (6×S) сравниваются вычислением коэффициента точностиК_m:

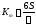
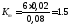
Кm>1, то точность процесса не соответствует требованиям чертежа.

После этого оценивается точность настройки технологического процесса сравнением допустимой погрешности настройки 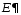и фактической:

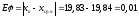
, имеет место брак.

Для принятия решения об изменении технологического процесса с целью повышения точности обработки детали, вычисляется вероятность брака. Для этого находится диапазон размеров, которые выходят за поле допуска и вычисляется вероятность попадания размеров в этот диапазон (Х_Н…Х_В):