19. Потери при внезапном расширении трубы (при).

Поток сам себе создаёт постепенно расширяющийся жидкий контур, в котором скорость уменьшается , ф статическое давление возрастает. Турбулентные пульсации подсасывают жидкость из кольцевого пространства расположенного между жидким контуром и стенкой трубы большего диаметра и в нём появляются вихри и обратные токи. Считаяи пренебрегая потерями на трение на 1-2 из-за малой его протяженности расчитаем потери при внезапном расширении несжимаемой жидкости. Можно записать уравнение Бернулли.

и выбирая ось отсчёта координаты z по оси трубы можно записать, что:

; ;.

, подставим (*) в последнее уравнение:

- потери на скорость

(**) – это теорема Борда – Кирно: Потери полного давления при внезапном расширении несжимаемой жидкости равны скоростному напору потерянной скорости, их ещё называют потерями на удар.

20.Течение газа в канале с внезапным расширением: при ρ≠const.

Будем рассматривать дозвуковое течение λ<1.

1)

2) →x

3)

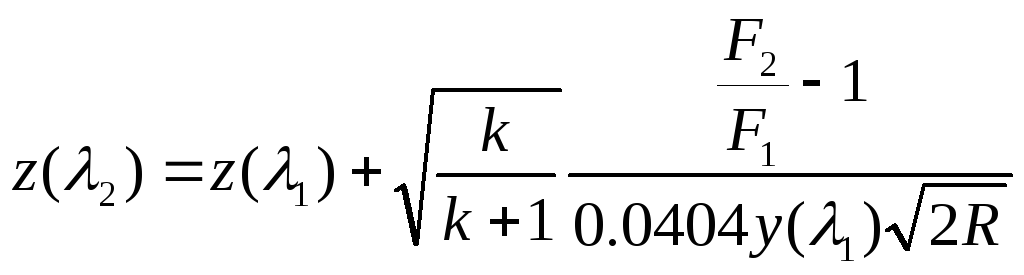
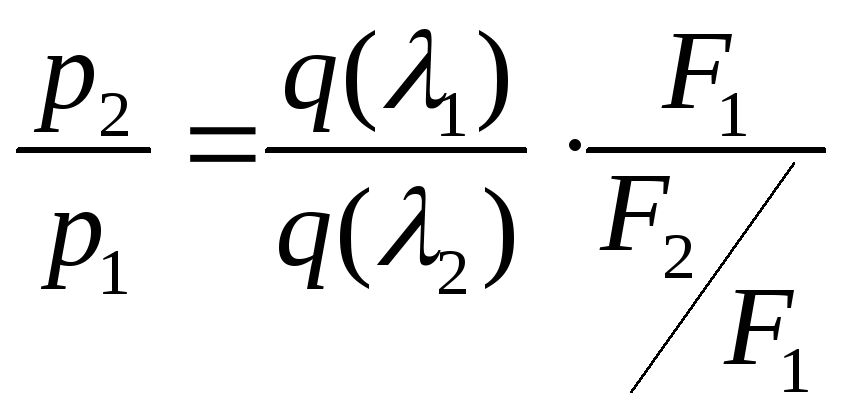
21. Уравнение энергии в форме энтальпии и его анализ.

; - потенциальная энергия уравнения. Для газа обычно.- полная энтальпия.- потенц. энергия,

- кинетическая энергия.

т.к. работа (трения) затрачивается на преодоление сил трения, диссинируется в теплоту и при адиаб. течении воспринимается самим газом, т.е., но противоположны по знаку => их из последнего уравнения можно исключить.

при =>

Все параметрыдолжны иметь один индекс.

Т.е. изменение полной энтальпии газа на участке 1-2 равно энергии с которой газ обменивается на данном участке с внешней средой.

Тогда для энергоизолир течения

Тогда для энергоизолированного течения ,=>в энергоизолир. течении энтальпия исохраняют пост. значение независимо от величины потерь, но наличие трения сказывается на характере термодинамических процессов протекающих в газе и проявляется при вычислении в ур-нии Бернулли интеграллаДля энергоизолированного течения ур-ние (*) можно записать в виде:, т.е. ускорение энергоизолированного потока происходит за счёт уменьшения энтальпии и сопров. понижением тем-ры. Единств. ист. ускорения или торможения газа для энергетически изолированного потока является разница давлений, она расходуется на преодоление трения

, при

; ,

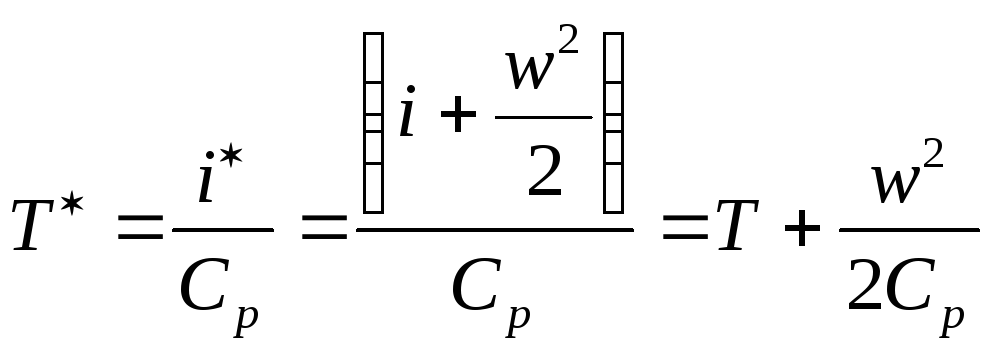
22. Преобразование полной энтальпии в кинетическую энергию потока. Максимальная скорость. Критическая скорость.

Для энергетически изолированного перевода газа из состояния покоя в состояние движения с параметрамиw, i ,T необходимо расходовать часть полной энтальпии . Формула для расчёта скорости течения газа:.

: При энергетически изолированном течении скорость будет достигнута тогда, когда полная энтальпия будет полностью превращена в кинетическую энергию, т.е. когда газ расшириться до абсолютного вакуумаT=0, p=0 и=0. Безразмерная скорость критическая скорость– это скорость потока, равная местной скорости потока.. все параметры становятся критическими (и т.д.);;;;;

23. Связь между характерными и безразмерными скоростями.

; , где- приведённая скорость – отн-е скорости потока к крит-й скорости.- отн-е ск-ти потока к макс-й ск-ти.

=> . Разделим на, =>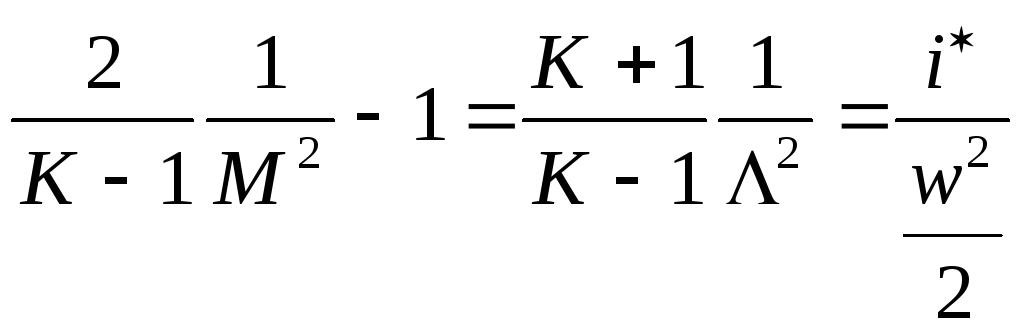безразмерные скоростихарактеризуют степень преобразования полной энтальпии газа в его кинетическую энергию в дан точке любого потока, т.е. имеют один физич смысл. => М/уесть однознач связь и задание одного из них опрт два других.