35 Формула тяги врд

36. Прямой скачок уплотнения. Вывод формулы для расчёта параметров течения за скачком уплотнения.

Прямой скачёк уплотнения – это скачёк, фронт которого перпендикулярен к векторам скорости перед скачком и заскачком. Прямой скачёк возникает, когда скорость газа при переходе через скачёк не меняет своего направления.

Течение энергоизо-лированное в струйке 1) скорость на прямом скачке уменьшается. 2) Ур-ние кол-ва движения в полных импульсах:;;За прямым скачком уплотнения скорость всегда дозвуковая:..

3) Увеличение газа,;

.4. Увеличение температуры газа .

5) Повышение давления

после преобразования , чем больше, тем сильнее скачёк; при,. Видно, что изменение всех параметров на скачке является функцией от;. В скачках уплотнения при ударном сжатии имеет место преобразование механической энергии в тепловую.

37. Косые скачки уплотнения. Треугольники скоростей на фронте скачка. Температура частичного торможения.

Косые скачки уплотнения – это скачки фронт которых составляет с вектором скорости сверхзвукового набегающего потока угол , отличный от прямого. КСУ возникают например при обтекании плоского клинка.

Скорость КС изменяется по величине и направлению, поэтому рассматривается треугольники скоростей. - угол фронт,- угол отклонения;;;

- угол между фронтом косого скачка и вектора скорости .,;;;.

КСУ можно представить как ПСУ для нормальной составляющей скорости сносимый вдоль фронта скачка со скоростью . КСУ можно рассчитывать как ПСУ. если в них все параметры (и т.д.) Заменить на пар-ры связанные с норм-ми составляющими скор-й () Температура частичного торможения – это температура, которую примет газ при не полном его торможении, а при частичномэнергоизолированном торможении только нормальная соситовляющая скорости. Такую темп-ру покажет термометр. движущийся вдоль скачка со скоростью .::;.

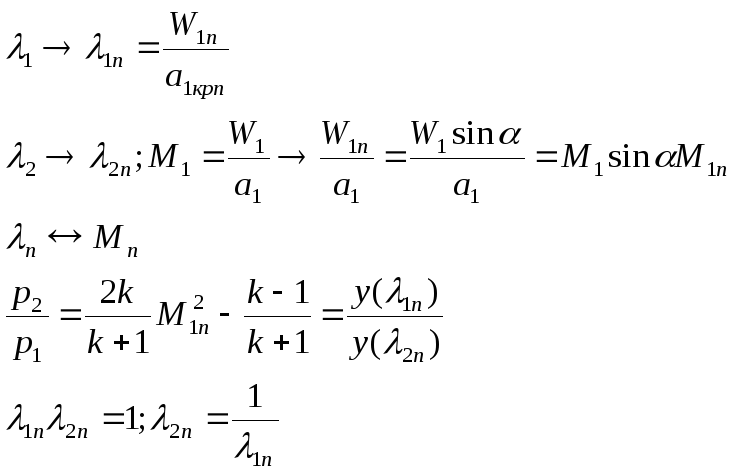
38. Отклонение потока в косом скачке. Диаграмма и её анализ.

; ;;;.

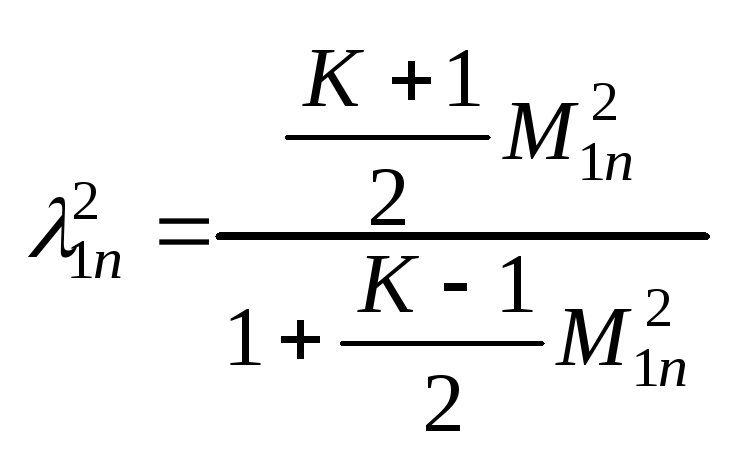- угол отклонения. Диаграмма - диаграмма зависимости угла КСУ от угла отклонения потока.

Одному и тому же числу M и углу отклонеия потока соотв. два возможных положения скачка. Скачки с меньшими углами(ветви 2-6) называются слабыми скачкамиусложнения, скорость за ними остаётся сверхзвуковой. ПриКСУ выражается в характеристики, на которых отклонения потока очень малы. В точкахв имеет место второй предел слабых скачков, за которыми . Скачки с большими(ветвив-а) называются сильными косыми скачками уплотнения, скорость за ними дозвуковая . принаблюдаются самые сильные КСУ. обычно на практике реализуются слабые косые скачки уплотнения (а-в).

т. а – общая для всех чисел М и соответствует прямому скачку.

т. с – разделяет область сильных скачков, за кот-ми М₂>1 М₂=λ₂=1

т. d – ограничивает снизу область слабых скачков ω=0, а α=α₁=arcsin(1/M₁)

При ω<ω_max устойчивыми являются только скачки, соответствующие участку bd.

39. Уравнение расхода газа через гдф: вывод. Характер измерения гдф, входящих в уравнении расхода.

для критического сечения струйки и для любого другого сечения;.

Введём ГДФ - приведённый расход.;

Каждому значению соответствуют два значения- одно меньше, другие больше единицы.

.

- пост. для данного газа к-т

;;