1. Методы Лагранжа и Эйлера для описания движения жидкости.

Есть два метода изучения движения жидкости: Лагранжа и Эйлера. В методе Лагранжа изучается движения каждой индивидуальной частицы, её путь, траектория, т.е. линия, по которой частица передвигается. Положение каждой частицы в момент времени t₀ задаётся координатами a,b,c. Движение опр-но, если изв-ны ф-и: или векторная функция:. Аргументa,b,c,t – переменные Лагранжа. Поток жидкости по Лагранжу описывается совокупностью траекторий отдельных частиц. По методу Эйлера изучается движение различных жидких частиц в фиксированных точках пространства. Скорость W задаётся как функция координат на оси – u,v,w; -переменные Эйлера. Между переменными Эйлера и Лагранжа есть связь:Можно найти поле ускорений

;

/=/ во времени

изменение скорости в пространстве

- оператор Набле.

следовательно ускорение можно представить в виде: .

В проекциях на оси координат

2. Закон сохранения массы. Уравнение неразрывности в интегральной и дифференциальной форме.

Выделим в жидкости произвольный замкнутый жидкий объём V, масса которого закон сохранения массы:.

Это уравнение справедливо для изолированной системы и выражает то, что масса произвольного изолированного объема с течение времени не изменяется, хотя сам объект может деформироваться. С помощью представлений Эйлера можно вывести уравнение неразрывности, выражающее закон сохранения массы. Рассмотрим поток жидкости через неподвижную пространственную область, объёмом V и ограниченную поверхностью F. Выделим площадку ,- единичный вектор внешней нормали иF секундная масса протекающая через dF:

. Если жидкость втекает в объём, то произведение отрицательно, а если вытекает – положительно.

Изменение массы в объёме V за единицу времени: в эл. объёмеdV измен. массы:

тогда секундное изменение массы в объёме V:. Приравняем последние уравнения. По формуле Острар Гаусса:- интегральное уравнение неразрывности.

- Дифференциальная форма уравнения неразрывности.

Если учесть, что:

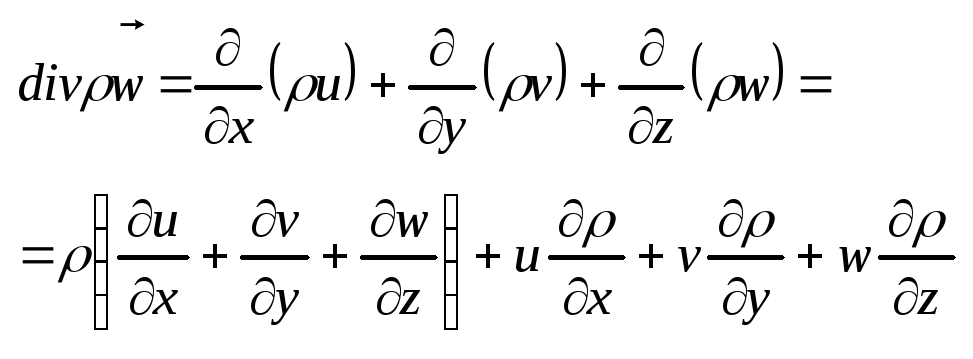
то: .

Для несжимаемой жидкости, где:

Для установившегося течения , т.е. для несжимаемой жидкости или для установившегося течения сжимаемой жидкости поток массы через замкнутый контр. поверхность равен 0.

3. Первая теорема Гельмгольца

Теорема: скорость перемещения любой точки жидкой частицы в данный момент времени можно рассматривать как результат сложения векторов скоростей поступательного, вращательного течения с полюсом О, находящегося в самой частице, и осью, проходящей через этот полюс, и скоростью деформационного движения, изменяющего скорость и размер частицы.

Доказательство:

Рассмотрим движение бесконечно малой жидкой частицы, имеющей форму параллелепипеда. С течением времени рёбра параллелепипеда могут скашиваться и растягиваться.

составляющие скорости движения частиц.

Точка a:

Точка d:

Точка b:

Точка e:

Рассмотрим скашивание ребра ab в плоскости xOy (из-за разности скоростей точек a и b вдоль оси x). За время dt скашивание характеризуется отрезком . Для ребраad: . Полное скашивание в точкеa: . Угловую деформацию принято характеризовать как ½ этой величины. Тогда скорость угловой деформации:;;;.

Поворот биссектрисы равен ,

Тогда условие скорости вращения ;;линейные деформации.

Рассмотрим удлинение ребра ad.

Разность скоростей точек a и d вдоль оси x: , удлинение:. Относительное удлинение:скорость относительного удлинения.

Перемещение частицы из точки а в точку g характеризуется радиус вектором: .

, ,

. Прибавим в правую часть () это скорость вращ. движения с угловой скоростью.

распишем и получим для:.

Аналогично:

, .

Это формулировка теоремы Гельмгольца: Первое слагаемое – поступательное движение: второе слагаемое и третье – деформационное движение (линейная, угловая). Последнее слагаемое – вращательное движение.