
|
|
|
Практика №1 |
|
Регрессионные модели |
|
|
Практика № 01.
Регрессионные модели
Решим на конкретном примере задачу регрессионного анализа, то есть, опираясь на имеющиеся экспериментальные данные, построим модель (определим функцию черного ящика), по которой вход преобразуется в выход (см. рис. П-01.1).
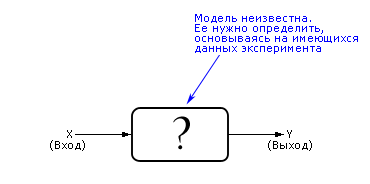
Рис. П-01.1. Схема одномерной регрессионной модели
Решение задачи регрессионного анализа
1) Пусть в результате проведения экспериментальных измерений мы получили набор из n = 8 экспериментальных точек. Отобразим их на рис. П-01.2.
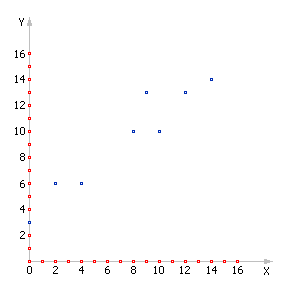
Рис. П-01.2. График экспериментальных данных
Занесем полученные данные в табл. П-01.1.
|
Таблица П-01.1. Экспериментальные данные |
|||||||||||||||||||||||||||
|
2)
Рассматривая экспериментальные данные,
предположим, что они подчиняются
линейному закону; выдвигаем гипотезу:
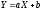 .
.
3) Запишем уравнение ошибки и суммарной ошибки:
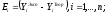
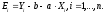
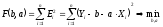
4)
Для нахождения экстремума приравняем
частные производные функции
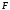 по переменным
по переменным
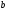 и
и
 к нулю (условие экстремума):
к нулю (условие экстремума):
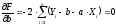
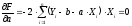
После раскрытия скобок получим систему из двух линейных уравнений:
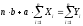
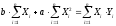
Для удобства вычислений составим табл. П-01.2.
|
Таблица П-01.2. Таблица промежуточных вычислений |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Для нахождения коэффициентов b и a методом Крамера представим систему в матричной форме:
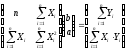
Подставляя конкретные значения из табл. П-01.2, получим:

Находим значения b и a:
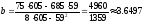
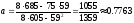
Итак, найденные значения b = 4960/1359 = 3.65 и a = 1055/1359 = 0.78 обеспечивают прохождение графика Y = aX + b как можно ближе одновременно ко всем экспериментальным точкам.
Таким образом, мы получили следующее линейное уравнение: Y = 0.78X + 3.65.
5) Теперь необходимо проверить, имеем ли мы право принять полученную гипотезу Y = 0.78X + 3.65 как верную, или же она должна быть отклонена. Для этого необходимо рассчитать ошибку Ei между точками заданной экспериментальной и полученной теоретической зависимости (см. табл. П-01.3), суммарную ошибку F и значение σ по формулам:
Ei = Yi – b – aXi, i = 1, …, n
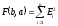
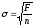
|
Таблица П-01.3. Вычисление ошибок между точками заданной экспериментальной и полученной теоретической зависимости |
|||||||||||||||||||||||||||||||||||||||||||||
|
Суммарная ошибка составляет:
F = 0.4225 + 0.6241 + 0.5929 + 0.0121 + 5.4289 + 2.1025 + 0.0001 + 0.3249 = 9.5080.
Значение σ = sqrt(9.5080/8) = 1.09. Найдем значение S = σ/cos(arctg(a)) = 1.09/cos(arctg(0.78)) = 1.38.
Если в полосу, ограниченную линиями Y = 0.78X + 3.65 – 1.38 и Y = 0.78X + 3.65 + 1.38 попадет 68.26% или более из всех экспериментальных точек, то можно сделать вывод о том, что наша гипотеза о линейности верна.
Окончательные рассчеты (см. табл. П-01.4) показывают, что 6 точек из 8 (то есть 75%) попадают в полосу, ограниченную линиями Y = 0.78X + 3.65 – 1.38 и Y = 0.78X + 3.65 + 1.38, из чего заключаем: зависимость между входом и выходом модели линейная, то есть выдвинутая нами гипотеза верна.
|
Таблица П-01.4. Проверка попадания точек внутрь заданного интервала |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Наконец, дадим графическую иллюстрацию нашим расчетам (рис. П-01.3).
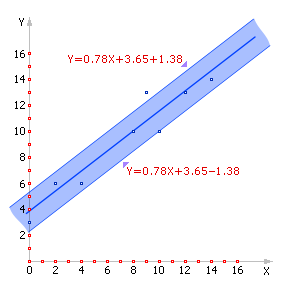
Рис. П-01.3. Найденная линейная зависимость с обозначенным интервалом [–S; +S]
В заключение отметим, что разобранный выше пример — учебный. Поэтому мы ограничились очень небольшим числом экспериментальных точек. В реальных условиях для обеспечения достоверности результатов исследования нужно брать гораздо большее число экспериментальных точек.
Варианты заданий:
Определить функцию черного ящика, по которой вход преобразуется в выход методом регрессионного анализа.
|
№1
|
№2
|
№3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
№4
|
№5
|
№6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
№7
|
№8
|
№9
|
Системы линейных уравнений
1. Основные понятия
Уравнение
называется линейным, если оно
содержит неизвестные только в первой
степени и не содержит произведений
неизвестных, т.е. если оно имеет вид  ,
,
где
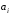 (
(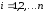 ),
),
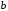 – числа.
– числа.
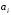 называются коэффициентами уравнения,
называются коэффициентами уравнения,
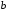 называется свободным членом. Если
называется свободным членом. Если
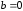 ,
то уравнение называется однородным.
В противном случае уравнение называется
неоднороным.
,
то уравнение называется однородным.
В противном случае уравнение называется
неоднороным.
В этом параграфе мы будем рассматривать
систему
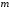 линейных уравнений с
линейных уравнений с
 неизвестными, т.е. систему вида
неизвестными, т.е. систему вида
 (1)
(1)
Обозначим через
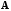 и
и
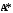 следующие матрицы:
следующие матрицы:
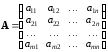 и
и
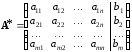 .
.
Матрицу
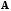 называют основной матрицей системы
(1), а матрицу
называют основной матрицей системы
(1), а матрицу
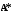 –
расширенной матрицей системы (1).
–
расширенной матрицей системы (1).
Пусть
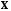 – матрица-столбец неизвестных,
– матрица-столбец неизвестных,
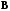 – матрица-столбец свободных членов,
т.е.
– матрица-столбец свободных членов,
т.е.
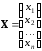 и
и
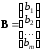 .
.
Тогда систему (1) можно записать в виде
матричного уравнения
 .
Его называют матричной формой
системы (1).
.
Его называют матричной формой
системы (1).
Упорядоченный набор чисел
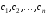 называется решением системы (1)
если он обращает в тождество каждое
уравнение системы. Если система линейных
уравнений имеет хотя бы одно решение,
то ее называют совместной. Система
линейных уравнений, не имеющая решений,
называется несовместной.
называется решением системы (1)
если он обращает в тождество каждое
уравнение системы. Если система линейных
уравнений имеет хотя бы одно решение,
то ее называют совместной. Система
линейных уравнений, не имеющая решений,
называется несовместной.
Если система совместна, то она имеет либо одно решение, либо множество решений. Система, имеющая единственное решение, называется определенной. Система, имеющая множество решение, называется неопределенной.
Критерии совместности и определенности системы дают следующие две теоремы
ТЕОРЕМА (Кронекера – Капелли). Система линейных уравнений (1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы, т.е.
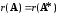 .
.
ТЕОРЕМА (критерий единственности решения). Система линейных уравнений (1) имеет единственное решение тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы и равен числу переменных, т.е.
 .
.
2. Методы решения систем линейных уравнений
1) Матричный метод.
ОПРЕДЕЛЕНИЕ. Обратной к матрице
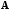 называется матрица, обозначаемая
называется матрица, обозначаемая
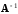 ,
такая, что
,
такая, что
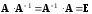 .
.
СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
1) Если
матрица
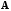 имеет обратную, то
имеет обратную, то
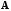 и
и
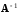 – квадратные одного порядка.
– квадратные одного порядка.
Действительно,
чтобы существовали произведения
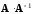 и
и
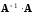 необходимо, чтобы матрицы
необходимо, чтобы матрицы
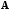 и
и
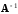 имели соответственно размеры
имели соответственно размеры
 и
и
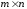 .
Тогда матрица
.
Тогда матрица
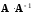 будет иметь размер
будет иметь размер
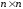 ,
а матрица
,
а матрица
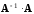 – размер
– размер
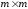 .
Но для равенства
.
Но для равенства
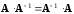 необходимо, чтобы размеры матриц
необходимо, чтобы размеры матриц
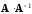 и
и
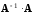 совпадали, т.е.
совпадали, т.е.
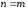 .
.
2) Если обратная матрица существует, то она единственная.
Действительно,
если предположить, что существует две
матрицы
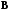 и
и
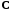 обладающие свойством
обладающие свойством
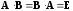 и
и
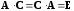 ,
,
то
будет существовать и произведение
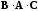 ,
причем
,
причем
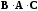

и
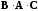
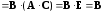 .
.
Следовательно, 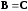 .
.
3) Если
матрица
 имеет обратную, то определитель матрицы
имеет обратную, то определитель матрицы
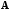 отличен от нуля.
отличен от нуля.
Действительно,
так как
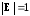 и для любых квадратных матриц
и для любых квадратных матриц
 и
и

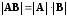 ,
то
,
то
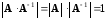
и,
следовательно,
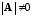 и
и
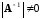 .
.
Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.
Условие
невырожденности матрицы
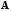 оказалось не только необходимым для
существования ее обратной матрицы, но
и достаточным. Т.е. справедлива следующая
теорема.
оказалось не только необходимым для
существования ее обратной матрицы, но
и достаточным. Т.е. справедлива следующая
теорема.
ТЕОРЕМА.
Пусть
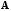 – квадратная матрица порядка
– квадратная матрица порядка
 .
Матрица
.
Матрица
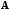 имеет обратную тогда и только тогда,
когда ее определитель
имеет обратную тогда и только тогда,
когда ее определитель
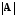 отличен от нуля. Причем обратная матрица
отличен от нуля. Причем обратная матрица
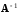 может быть найдена по формуле:
может быть найдена по формуле:
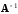
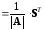 ,
,
где
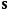 – матрица из алгебраических дополнений
элементов матрицы
– матрица из алгебраических дополнений
элементов матрицы
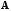 ,
т.е.
,
т.е.
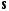
 .
.
Матрица
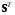 называется союзной (или
присоединенной, или взаимной)
для матрицы
называется союзной (или
присоединенной, или взаимной)
для матрицы
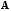 .
.
ПРИМЕР. Найти матрицу, обратную к матрице
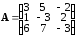 .
.
Так
как определитель матрицы
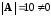 ,
то матрица имеет обратную. Найдем
алгебраические дополнения элементов
матрицы
,
то матрица имеет обратную. Найдем
алгебраические дополнения элементов
матрицы
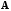 .
Получим:
.
Получим:
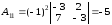 ,
,
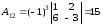 ,
,
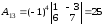 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
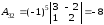 ,
,
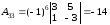 .
.
Следовательно, 
и 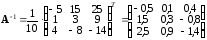 .
.
Рассмотрим
теперь систему линейных уравнений, в
которой число уравнений
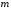 и число неизвестных
и число неизвестных
 совпадает и
совпадает и
 .
Тогда:
.
Тогда:
1)
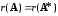
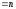 и, следовательно, такая система имеет
единственное решение.
и, следовательно, такая система имеет
единственное решение.
2)
Матрица
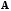 имеет обратную матрицу
имеет обратную матрицу
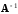 .
.
Покажем,
как можно найти решение этой системы с
помощью обратной матрицы
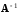 .
Запишем систему в матричной форме:
.
Запишем систему в матричной форме:
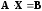 (2)
(2)
Умножим
обе части равенства (2) на
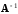 слева. Получим:
слева. Получим:
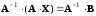 ,
,
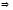
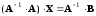 ,
,
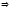
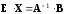 ,
,
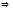
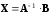 . (3)
. (3)
Таким
образом, если в системе линейных уравнений
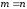 и
и
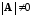 ,
то система имеет единственное решение,
которое можно найти по формуле (3).
Нахождение решения по формуле (3)
называют матричным методом
решения системы.
,
то система имеет единственное решение,
которое можно найти по формуле (3).
Нахождение решения по формуле (3)
называют матричным методом
решения системы.
ПРИМЕР. Решить матричным методом систему
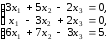
Матрица системы имеет вид
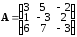 .
.
Эта
матрица невырожденная (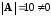 ),
и, следовательно, решение может быть
найдено матричным методом. Имеем (см.
предыдущий пример):
),
и, следовательно, решение может быть
найдено матричным методом. Имеем (см.
предыдущий пример):
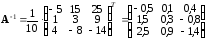
и 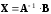
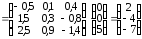 .
.
Таким
образом, получили
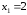 ,
,
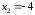 ,
,
 .
.
