Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таразский государственный университет им. М.Х. Дулати

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika-2_Tmo_ee_aiu_ret__3_3_Kr_Rus_2015

.pdf

Скачиваний:

Добавлен:

06.03.2016

Размер:

1.69 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Документ СМК	Ф 11/13-1.04-2015

Тестовое задание	Редакция 4
Тестовое задание	Дата введения 10.01.2015
	Дата введения 10.01.2015

ТАРАЗСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ М.Х. ДУЛАТИ

Кафедра «Математика»

Тестовое задание (2015г.) №

По дисциплине «Математика-2» (3 кредита) (3+3)

Для студентов 1 курса, специальностей

5В072400-«Технологические машины и оборудование», 5В071800-«Электроэнергетика», 5В070200- «Автоматизация и управление», 5В071900-«Радиотехника электроника и телекоммуникации»,

1. Найти область определения функции z ln(4 4x y 2 )

А) внутренняя часть параболы y 2 4x 4 , кроме точек параболы

B) внешняя часть параболы y 2 4x 4 ,

включая точки параболы С) вся плоскость, кроме точек параболы

D) внутренняя часть параболы y 2 4x 4 , включая точки параболы

E) внешняя часть параболы y 2 4x 4 , кроме точек параболы

2. Найти область определения функции

z	1


	1 x2 y 2
	1 x2 y 2

А) внутренняя часть окружности x 2 y 2 1, кроме точек окружности

B) внутренняя часть окружности x 2 y 2 1, включая точки окружности

С) внешняя часть окружности x 2 y 2 1, включая точки окружности

D) точки окружности x 2 y 2 1

E) внешняя часть окружности x 2 y 2 1, кроме точек окружности

3. Найти область определения функции z y x :

А) полуплоскость x 0 B) полуплоскость x 0

С) полуплоскость x 0 D) полуплоскость x 0 E) полуплоскость x 0

4. Найдите значение функции

z 3x 2 y 2x 2xy2 5 в точке P 0, 4 :

А) 5

B) 1

С) 0

D)7

E)17

5. Найдите значение функции

z х у х z у z в точке P 1, 2,3

А) -2 B) -14 С) -10 D) 30 E) 2

6. Вычислить предел lim		x 2		y 2

	4 x		2	y	2	2
x 0	4 x			y		2
x 0
y 2
A) -4
B) 9
C) 18
D) -40
E)

7. Вычислить предел lim	x2	( y 2)2 1 1
7. Вычислить предел lim		x2	( y 2)2
x 0		x2	( y 2)2
y 2

A)12

B)0

D)9

E)20

8. Функция z f (x, y) непрерывная в каждой

точке некоторой области D называется.. А) непрерывной в области D

B) дифференцируемой в области D С) ограниченной в области D

D) кусочно-непрерывной в области D E) монотонной в области D

9. По формуле dz fx dx fy dy вычисляется

А) полный дифференциал функции z f (x, y) B) частная производная от функции z f (x, y) по переменной x

С) частная производная от функции z f (x, y) по переменной у

D) частный дифференциал функции z f (x, y) E) частный дифференциал функции

u f (x, y, z)

10. Полный дифференциал функции

u f (x, y, z) вычисляется по формуле

A)	du	f	dx	f	dy	f	dz
		x		y		z
B)	du	f	x	f	y	f	z
		dx		dy		dz
C)	du	f	f		f
		x	y		z

D)du dx dy dz

E)du fx dx fy dy

11.Функция, имеющая дифференциал в каждой точке некоторой области D называется

А) дифференцируемой в области D B) непрерывной в области D

С) кусочно-непрерывной в области D D) убывающей в области D

Е) неограниченной в области D

12.Найти fx функции f x2 e3y sin x :

А) 2x cosx

В) 3e3 y

С)

D) cos x

E) 30

13. Найти

дf

функции f

x y

ду

А)

(х у)2

2 у

(х у)2

С)

(х у)2

2 у

(х у)2

(x y)2

14. Найти

f ( 1;1) функции f е3x 2 у :

А) 3е

B) 3е

С) - 2е

D) - 2е 1

Е) 2е 2

дf

х 2

15. Найти

функции f

ду

А)

С)

у 2

х 2

Е)

у 2

х 2

16. Найти

дf

функции f

х у :

ду

А) х у nх

B) ух у 1

С) х у nу

D) xxу 1

Е) у nх

дf

17. Найти ду функции f arctg(xy) :

A) 1 х 2 у 2

B) 1 х 2 у 2

1 C) 1 х 2 у 2

D) cоs2 (xу) E) arctg х

18. Найти df (1;1) функции f ух2 :

А) dx 2dу

1 1

B)2 dx 2 dу

С) dx 2dу

D) dx dу

Е) f 12 dx dy

19. Найти df (1;2;0) функции f n(xy z) :

А) dx 12 dy 12 dz

B)dx 2dy dz

C)12 dy 2dz

D)2dx 2dy

E)12 dx dy dz

20. Найти df ( 1;1) функции f е3х 2 у :

А) 3dx 2dy е 5

B)dx dy е 5

C)3dx 2dy е 1

D)2dx 3dy е 1

E)dx dy е5

21. Если z f (x, y) - дифференцируемая функция своих аргументов x и y , а x x(t) и y y(t) являются дифференцируемыми функциями от аргумента t , то производная

сложной функции z f (x(t), y(t)) находится по формуле:

A) dz z dx z dy dt x dt y dt

B)dzdt dxdz dxdt dydz dydt

C)dz z x z y dt x t y t

22. Если z f (x, y)

- дифференцируемая

функция своих аргументов x и y , а x x(u, ) и

y y(u, ) , то частная производная z сложнойu

функции z f (x(u, ), y(u, )) находится по

формуле:

A) z z x z yu x u y u

B) z dz x dz y

u dx u dy u

C) z z dx z dy

u x du y du

D) z x yu u u

E) z z zu x y

23. Если z f (x, y) - дифференцируемая функция своих аргументов x и y , а x x(u, ) и

y y(u, ) , то частная производная z сложнойv

функции z f (x(u, ), y(u, )) находится по формуле:

E) z dz x dz ydx dy

24. Функция z z(x, y) называется неявной функцией от x и y , если она задается уравнением..

A)F (x, y, z) 0

B)F (x, y) 0

C)F ( y, z) 0

D)F (x, y, z) C

E)Z (x, y) C

25. Частной производной z неявной функции

z z(x, y) :

A) z Fx'

x Fz'

B)z Fx'

x Fz'

C)z Fx'x

D)z F

x Fx'

E)z Fx'

x F

26. Указать формулу нахождения частной

производной z неявной функции z z(x, y) :y

A) z Fy'

x Fz'

B)z Fy'

x Fz'

C)z F

x Fy'

D)z Fy'x

E)z Fy'

x F

27. Указать неявные функции z z(x, y) :

x 2 y 2 z 2 2xz 1; z x 2 y 2 ; 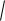x 2 3y 2 2

A) x 2 y 2 z 2 2xz 1; xyz3 x y z

B) x 2 y 2 z 2 2xz 1;

z 3xyz a

C)z x 2 y 2

D)z x2 y 2 ; xyz3 x y z

E) 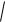x2 3y2 2 y2 x3 ; z 3xyz a

28. Полный дифференциал неявной функции z z(x, y) находится по формуле:

A) dz xz dx yz dy

B) dz z z

x y

C)dz dxdz dx dydz dy

D)z xz dx yz dy

E)dz dxdz dydz

29. Найти dzdt функции z 4x 3 xy y 2 , где x t 2 , y 3 2t :

A)dzdt 6t 5 6t 2 8t

B)dzdt 3t 4 t 2 6t

C)dzdt 6t 5 4t 4 4t 3 8t

D)dzdt 2t 2

E)dzdt 12t 2 8t

30. Найти dzdt функции z e xy , где x 3t 1, y t 1:

2(3t 2)e (3t 1)(t 1)

e(3t 1)(t 1)

4 e(3t 1)(t 1)

2(5t 1)e(3t 1)(t 1)

y z

; z 3xyz a; xyz

3(t 1)e(3t 1)(t 1)

31. Найти частную производную

функции z x ln y , где x u v ,

A)	z			u	ln u
	u			u

B)	z		u		ln u
	u

C)	z	ln u				u
	u					u

D)z ln uu

E)z (1 u ) ln uu

32. Найти частную производную функции z x ln y , где x u ,

z сложной

y u v :

z сложной

y u :

A)	z			u	ln u


B)	z		u		ln u

				u
C)	z	ln u				u
						u

D)z 1 u

E)z (u ) ln u

33. Найти частную производную z сложной

функции z x2 y , если x u 2v , y 2u v :

A)z 2(u 2 )(3u )

B)z (u 2 )(2 u 2 )u

C)z 3u

D)z 2(u 2 )2u

E)z (u 2 )(2u 4 7u 6 2 )u

34. Найти частную производную z сложной функции z x2 y , если x u 2v , y 2u v :

A) z (2 u)(7u 6 )

B)		z	5u(u 2 )
B)			5u(u 2 )

C)		z	(u 2 )(6u 2	8u u 4 2 2 )
C)	u		(u 2 )(6u 2	8u u 4 2 2 )
	u
D)		z	(u 2 )(9u 2 )
D)			(u 2 )(9u 2 )

E)		z	1
E)			1

35. Найти частную производную	z	сложной
	u

функции z x xy , если x u ,		y u :

A)z 2u 1u

B)z 1 uu

C)z 2uu

D)z 1 2u 2 2u

E)z (u )(u 1)u

36. Найти частную производную z сложной функции z x xy , если x u , y u :

A)z 1 2

B)z 1 2u

C)z 2

D)z 1 2

E)z 1 2u u 2 u 2 2

37. Найти частную производную z неявной

функции z 3 3x 2 y 5 :

A)	z	2xy
	x	z 2

B)z 6xy

C)z 6xyx z 3


D)	z		2xy
	x		3z 2

E)	z	2x
	x		z 2

38. Найти частную производную функции z3 3x2 y 5 :

A)	z	x 2
	y	z 2

B)z 3x2y

C)z x 2 y

y z 2

D) z 3x2

y z 3

E)z 3(x 2 z 2 )y

39. Найти частную производную функции xz y 2 z 2 0

A)	z	z
	x	x 2 y 2 z

B)z zx


C)	z		x
C)	x	x	2z
	x	x	2z
D)	z			x
D)	x		x 2 y 2 z 2
	x		x 2 y 2 z 2
E)	z		x 2 y 2 z
E)	x		z
	x		z

40. Найти частную производную функции xz y 2 z 2 0

A)	z	2 yz2
	y	x 2 y	2 z

B)z 2 yz2y

C)	z	yz2
	y	x 2 y 2 z

D)z 2 yy

z неявной

E)	z	x 2 yz2 z
	y		2 yz	2

41. Найти			2 z	функции z x3 y 2xy2 :
			x 2

A)2 z 6xyx 2

B)2 z 2 y(3x 2)x2

C)2 z 2 y(3x y)x 2

D)2 z 6xx 2

E)2 z 6 yx 2 y 2x 2

2 z

42.Найти y x функции z sin xy :

A)		2 z	cos xy xysin xy
A)		y x	cos xy xysin xy
		y x
B)		2 z	x2	sin xy
B)	y x		x2	sin xy
	y x
C)		2 z	cos y
C)	y x		cos y
	y x
D)		2 z	cos xy y sin xy
D)		y x	cos xy y sin xy
		y x
E)		2 z	sin xy
E)	y x		sin xy
	y x
			2 z
43. Найти y 2				функции

z 4x3 3x2 y 3xy2 y3

A)2 z 6(x y)y 2

B)2 z 4x3 3x 2 6x 6 yy 2

C)2 z 2(x 3y)y 2

D)2 z 2 y(3 x)y 2

E)2 z 3x 2 3y 2 6xyy 2

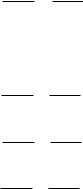
44. Найти				2 z		функции	z x3 y 2 xy5 5x y
44. Найти				x y		функции	z x3 y 2 xy5 5x y
				x y
A)		2 z	6x2 y 5y 4
A)		x y	6x2 y 5y 4
		x y
B)		2 z	2x3 20xy3
B)	x y		2x3 20xy3
	x y
C)		2 z	6x		2 y
C)	x y		6x		2 y
	x y
D)		2 z	3x		2 y 5y5
D)		x y	3x		2 y 5y5
		x y
E)		2 z	5y 4
E)	x y		5y 4
	x y

45. Укажите все частные производные второго порядка функции z f (x, y) :

А)

2 z

x 2

x y

y x

y 2

2 z

x 2

y 2

С)

2 z

x y

y 2

2 z

y ,

y x

3 z

2 z

Е)

x ,

x 2 y

y 2

46. Если смешанные частные производные

второго порядка

2 z

непрерывны, то

x y

y x

они…

2 z 2 z

A)x y y x

B)	2 z	2 z
	x y	y x

C)2 z 2 z Cx y y x

D)2 z 2 z 1x y y x

E)2 z 2 z zx y y x

47. Указать формулу вычисления дифференциала второго порядка d 2 z для функции z f (x, y) :

d 2 z

dx2

2 f

dxdy

2 f

dy2

x 2

x y

y 2

d 2 z

2 f

dxdy

dy2

x 2

y 2

x y

d 2 z

d 2 f

x 2 2

d 2 f

x y

d 2 f

y 2

dx2

dx y

dy2

D) d 2 z

dx2

x y

d 2 z

2 f

dy2

x y

y 2

48. Указать необходимые условия экстремума в точке Р(х0 , у0 ) функции z f (x, y) :

		f x ,						y
					0				0		0
			x								0
А)			x
		f x , y							0
					0				0		0
			y								0


		2 f x						, y				0
B)							0			0		0
B)			x 2
		f x0 , y0 0
		f x0 , y0 0
С)		2 f x			0	, y			0		0
С)					0				0		0
		y 2
		f (x0 , y0 )									0
			x								0
D)			x
D)				2		f
						f			0
			x y						0
			x y

	2 f x0							, y0				0

			x				2
E)			x
E)	2 f x0							, y0
	2 f x0							, y0				0
			y				2					0
							2

49. Если стационарная точка Р0 (х0 , у0 ) является точкой минимума функции z f (x, y) и

A z	xx	P	, B z	xy	P ,	C z	yy	P ,	AC B 2
	xx	0		xy	0		yy	0
, то…
А) 0,			A 0
B) 0,			A 0
С) 0,			A 0

D) 0,	A 0
Е) 0,	A 0

50. Если стационарная точка Р0 (х0 , у0 ) является точкой максимума функции z f (x, y) и

A z	xx	P	, B z	xy	P	, C z	yy	P ,	AC B 2
	xx	0		xy	0		yy	0
, то…
А) 0,			A 0
B) 0,			A 0
С) 0,			A 0
D) 0,			A 0
Е) 0,			A 0

51. Найти стационарную точку Р(х0 , у0 ) функции z x2 xy y 2 x y 1 :

A)P( 1;1)

B)P( 1;3)

		1		1
C)	P		;

		2		2

D)P ;2 3

E)P(0; 0) 1

52. Найти точку экстремума Р(х0 , у0 ) функции z (x 2)2 2 y 2 10 :

A)P(2; 0) точка максимума

B)P(7; 0) точка максимума

C) не имеет точек экстремума

D)P( 2; 0) точка максимума

E)P( 2;1) точка максимума

53. Найти стационарную точку Р(х0 , у0 )

функции z x2 xy y 2 9x 6 y 20 :

A)P( 4;1)

B)P(8; 7)

		2	2		1
C)	P			; 4

			5		5

D)P 4 ;32

E)P( 8; 1)1

54. Найти точки экстремума Р(х0 , у0 ) функции z x2 y 2 xy x y :

A) P( 1; 1) точка максимума

1 1

B)P ; точка максимума

3 3

C)P(1; 1) точка максимума

1 1

D)P ; точка максимума

3 3

E) P( 3; 1) точка максимума

55. Наибольшее значение функции

z y x 2 y 2 x 14 y в точке максимума

P(4; 4) равно:

A)28

B)-1

C)4

D)-20

E)7

56. Найти точку Р(х0 , у0 ) , в которой функция

z x2 xy y 2 6x 9 y принимает наименьшее значение:

A)P(1; 4)

B)P(17; 4)

C)P(3; 92)

D)P( 7;8)

E)P(5; 7)

57. Найти стационарную точку Р(х0 , у0 ) функции z 1 6x x2 xy y 2 :

A)P(4; 2)

B)P( 4; 2)

C)P(3; 0)

D)P(15; 3)

	14		;	7
E)	P
E)	P
		3		3

58. Наибольшее значение функции

z xy(6 x y) в точке максимума P(2; 2) равно:

A)8

B)2

C)4

D)-4

E)-1

59. Найти точку Р(х0 , у0 ) , в которой функция

z xy x 2 y 2 9 принимает наибольшее значение:

A) P(0; 0)

	18		;	9
B)	P
B)	P
		5		5

C)P(0; 2)

D)P2 (2;0)

E)P(0; 2)

60. Наименьшее значение функции

z x2 y xy x y в точке минимума P( 1; 1) равно:

A)-1

B)10

C)50

D)-40

E)0

61.Уравнение называется дифференциальным относительно некоторой искомой функции, если оно содержит…

A) хотя бы одну производную искомой функции B) только одну производную искомой функции C) производные 1-го и 2-го порядка искомой функции

D) производную 1-го порядка искомой функции E) аргумент и производную 2-го порядка искомой функции

62.Дифференциальное уравнение называется обыкновенными, если…

A) искомая функция y является функцией

одного аргумента x

B) искомая функция y зависит от нескольких аргументов

C) искомая функция y является четной функцией

D) искомая функция y является монотонной функцией

E) искомая функция y зависит только от двух аргументов

63. Дифференциальным уравнением первого порядка называется уравнение вида…

A)F (x, y, y ' ) 0

B)F (x, С) 0

C)F (x, y, y ' ) C

D)F (x, y) 0

E) F (x, y ' ,С) 0

64. Общим решением дифференциального уравнения первого порядка называется функция…

A)y x, C

B)y x

C)y f (x, y)

D)y x

Е) y (C)

65. Общий интеграл дифференциального уравнение первого порядка имеет вид:

A)Ф(x, y, C) 0

B)y (x, C)

C)Ф(x, y) C

D)y (x, C)

E)F (x, y' ,C) 0

66.Порядок дифференциального уравнения совпадает …

A) с порядком наивысшей производной, входящей в уравнение

B) со степенью аргумента x искомой функции C) с числом равным сумме производных функции, входящей в уравнение

D) с порядком низшей производной, входящей в уравнение

E) со степенью искомой функции в уравнении

67.Дифференциальное уравнение вида

x M 2 y dx N1 x N 2 y dy 0 называется…M1

А) уравнением с разделяющимися переменными В) однородным уравнением

C)линейным уравнением

D)уравнением Бернулли

E)уравнением Лагранжа

68. Укажите уравнения с разделяющимися переменными

а) y / 2ху	б) y /	у	е х	в) y / y(1 х)
а) y / 2ху	б) y /	х	е х	в) y / y(1 х)
		х
A) а,в
B) б
С) а,б
D) б,в
E) а,б,в

69. Дифференциальное уравнения вида

	/		y
y		f		называется..

			x

А) однородным уравнением В) линейным уравнением

C)уравнением Бернулли

D)уравнением Клеро

E) уравнением с разделяющимися переменными

70. Для решения однородного уравнения применяется подстановка :

A)y ux , где u u(x) -неизвестная функция

B)y uv , где u u(x) , v v(x) -неизвестные функции

С) y ux , где u u(x) -неизвестная функция

D)y uv , где u u(x) , v v(x) -неизвестные функции

E)y 1z , где z z(x) -неизвестная функция

71. Функция f (x, y) называется однородной измерения m относительно x и y , если

A)f ( x, y) m f (x, y)

B)f ( x, y) m 1 f (x, y)

C)f ( x, y) mf (x, y)

D)f ( x, y) m f (x, y)

E)f ( x, y) f (x, y)

72. Определить вид дифференциального уравнения x 2 y / y 0 :

А) уравнение с разделяющимися переменными В) однородное уравнение

C)линейное уравнение

D)уравнение Бернулли

E) уравнение в полных дифференциалах

73. Найдите общее решение дифференциального уравнения 2xydx dy 0 :

А)	y Ce x2
В)	y e x2
С)	y e x

D) e x2 1 y

Е) y e x2

74. Найдите общее решение дифференциального уравнения e x 3 y dy dx

	3 y			1
A) e		3 C
				e x

B) e3 y 3 e x C
C) e 3 y			x

		3
D) e3 y		e x C

E) e3 y 13 (x ln C)

75. Найдите частное решение дифференциального уравнения xdy ( y 5)dx, y(1) 1

A)y 6x 5

B)y 4x 5

C)y x 5

D)y x

E)y 4x 5

76. Определить вид дифференциального уравнения y xy/ 1 x2 y :

A) уравнение с разделяющимися переменными B) уравнение в полных дифференциалах

С) уравнение Бернулли

D)однородное уравнение

E)линейное уравнение

77. Определить вид дифференциального

уравнения xy/ y xe x :

A) однородное уравнение B) линейное уравнение

С) уравнение с разделяющимися переменными

D)уравнение в полных дифференциалах

E)уравнение Бернулли

78. Найдите общее решение дифференциального

уравнения dy x 2 y : dx x

A)y x(xC 1)

B)y x(1 x 2 2C )

C)y x 2 C

D)y 3x (3xC 1)

E)y x(3xC 1)

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.03.2016434.69 Кб32dinarbook-russian.pdf
#
06.03.201626.46 Кб68GREAT BRITAIN реферат.docx
#
06.03.20161.05 Mб10imp 2013-2014. rus.doc
#
06.03.2016140.8 Кб4Istoria.doc
#
06.03.201647.97 Кб23matanaliz.docx
#
06.03.20161.69 Mб17Matematika-2_Tmo_ee_aiu_ret__3_3_Kr_Rus_2015.pdf
#
06.03.2016322.05 Кб8Maтериаловедение.doc
#
06.03.2016354.02 Кб9mishina_-_logistika._konspekt_lekciy.pdf
#
06.03.20161.96 Mб25NSU-Конспект лекции каз.doc
#
06.03.2016243.71 Кб4nura SMO.doc
#
06.03.2016291.82 Кб72Rukovodstvo_dlya_nizhnikh_bondazhistov_i_bondazhnykh_modeley.pdf