Математика-2 ТМО+ЭЭ+АиУ+РЭТ (3+3 кр) рус 2015
.docA)
B)
С)
D)
E)
102.
Сколько произвольных постоянных может
содержать общее решение уравнения вида
A)
B) 1
С)
D)
E) 2
103.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
104.
К какому виду преобразуется уравнение
после подстановки
A)
B)
С)
D)
E)
105.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
106.
К какому виду преобразуется уравнение
после подстановки:
A)
B)
С)
D)
E)
107.
Определить порядок дифференциального
уравнения
A) 3
B) 22
С) 51
D) 13
E) 6
108.
Определить порядок дифференциального
уравнения
A) 4
B) 2
С) 6
D) 3
E) 1
109.
Определить порядок дифференциального
уравнения
A) 3
B) 20
С) 10
D) 40
E) 5
110.
Найти общее решение уравнения
A)
B)
С)
D)
E)
111.
Решите уравнение
А)
В)
С)
D)
Е)
112.
Решите уравнение
A)
B)
C)
D)
Е)
113.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
114.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
115.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
116.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
117.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
118.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
119.
Для решения дифференциального уравнения
применяется подстановка:
A)
B)
С)
D)
E)
120.
Если
и
частные решения линейного дифференциального
уравнения 2-го порядка с постоянными
коэффициентами
,
то его общее решение имеет вид:
A)
B)
С)
D)
E)
121.
Частные решения
и
линейного дифференциального уравнения
2-го порядка с постоянными коэффициентами
дифференциального уравнения
обладают свойством…
A)
B)
С)
D)
E)
122.
Если корни
и
характеристического
уравнения действительны и различны
(
),
то общее решение дифференциального
уравнения
имеет вид:
A)
B)
С)
D)
E)
123.
Если корни
и
характеристического
уравнения действительны и равны (
),
то общее решение дифференциального
уравнения
имеет вид:
A)
B)
С)
D)
E)
124.
Если корни
и
характеристического
уравнения комплексно сопряженные числа
(
),
то общее решение дифференциального
уравнения
имеет вид:
A)
B)
С)
D)
E)
125.
Общее решение неоднородного линейного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами
имеет вид:
A)
B)
С)
D)
E)
126.
Если правая часть дифференциального
уравнения
имеет вид
,
где
-
многочлен
-й
степени и
не
является корнем характеристического
уравнения, то частное решение
имеет
вид (
-
многочлен
-й
степени):
A)
B)
С)
D)
E)
127.
Если правая часть дифференциального
уравнения
имеет вид
,
где
-
многочлен
-й
степени и
является корнем характеристического
уравнения кратности
,
то частное решение
имеет
вид (
-
многочлен
-й
степени):
A)
B)
С)
D)
E)
128.
Если правая часть дифференциального
уравнения
имеет вид
,
где
,
-
многочлены
-й
степени и
не
является корнем характеристического
уравнения, то частное решение
имеет
вид (
,
- многочлены
-й
степени):
A)
B)
С)
D)
E)
129.
Если правая часть дифференциального
уравнения
имеет вид
,
где
,
-
многочлены
-й
степени и
является корнем характеристического
уравнения кратности
, то частное решение
имеет
вид (
,
- многочлены
-й
степени):
A)
B)
С)
D)
E)
130.
При решении неоднородного дифференциального
уравнения 2-го порядка с постоянными
коэффициентами
методом Лагранжа неизвестные функции
определяются из системы уравнений:
A)
B)
C)
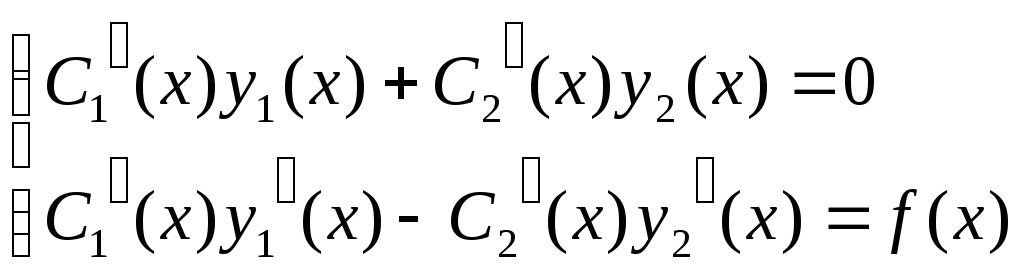
D)
E)
131.
Найти общее решение дифференциального
уравнения
A)
B)
C)
D)
E)
132.
Найти общее решение дифференциального
уравнения
A)
B)
C)
D)
E)
133.
Найти общее решение дифференциального
уравнения
A)
B)
C)
D)
E)
134.
Найти общее решение дифференциального
уравнения
A)
B)
C)
D)
E)
135.
Найти общее решение дифференциального
уравнения
A)
B)
C)
D)
E)
136.
Найти общее решение дифференциального
уравнения
A)
B)
C)
D)
E)
137.
Определить вид частного решения
дифференциального уравнения
A)
B)
C)
D)
E)
138.
Определить вид частного решения
дифференциального уравнения
A)
B)
C)
D)
E)
139.
Определить вид частного решения
дифференциального уравнения
A)
B)
C)
D)
E)
140.
Определить вид частного решения
дифференциального уравнения
A)
B)
C)
D)
E)
141.
Предел интегральных сумм
при
условии
,
где
-диаметр
ячейки
называется
А)
двойным интегралом от функции
по
области
В)
повторным интегралом от функции
по
области
С)
поверхностным интегралом от функции
по
координатам
D)
криволинейным интегралом первого рода
от функции
по
области
Е)
криволинейным интегралом второго рода
от функции
по
области
142.
Двойной интеграл от функции
по замкнутой ограниченной области
в
декартовых координатах имеет вид:
A)
B)
C)
D)
Е)
143. Какие функции интегрируемы в смысле двойного интеграла?
A) функции, непрерывные в ограниченной области
B) функции, монотонные в ограниченной области
C) разрывные функции в ограниченной области
D) функции, кусочно-непрерывные
E) функции, неограниченной области.
144. Укажите свойство двойного интеграла:
A)
B)
,
где
- площадь области
C)
D)
E)
145. Укажите свойство двойного интеграла (С-постоянная):
A)
B)
C)
D)
Е)
146.
Если область интегрирования
двойного
интеграла разбита на две области
и
,
то
равен..