Математика-2 ТМО+ЭЭ+АиУ+РЭТ (3+3 кр) рус 2015
.doc|
Документ СМК |
Ф 11/13-1.04-2015 |
|
|
Тестовое задание |
Редакция 4 |
|
|
Дата введения 10.01.2015 |
Таразский государственный университет имени М.Х. Дулати
Кафедра «Математика»
Тестовое задание (2015г.) №
По дисциплине «Математика-2» (3 кредита) (3+3)
Для студентов 1 курса, специальностей
5В072400-«Технологические машины и оборудование», 5В071800-«Электроэнергетика», 5В070200- «Автоматизация и управление», 5В071900-«Радиотехника электроника и телекоммуникации»,
1.
Найти область определения функции
А)
внутренняя часть параболы
,
кроме точек параболы
B)
внешняя часть параболы
,
включая точки параболы
С) вся плоскость, кроме точек параболы
D)
внутренняя часть параболы
,
включая точки параболы
E)
внешняя часть параболы
,
кроме точек параболы
2.
Найти область
определения функции
А)
внутренняя часть окружности
,
кроме точек окружности
B)
внутренняя часть окружности
,
включая точки окружности
С)
внешняя часть окружности
,
включая точки окружности
D)
точки окружности
E)
внешняя часть окружности
,
кроме точек окружности
3.
Найти область определения функции
:
А)
полуплоскость
B)
полуплоскость
С)
полуплоскость
D)
полуплоскость
E)
полуплоскость
4.
Найдите значение функции
в
точке
:
А)
B)
С) 0
D)
E)
5.
Найдите значение функции
в точке
А) -2
B) -14
С) -10
D) 30
E) 2
6.
Вычислить предел
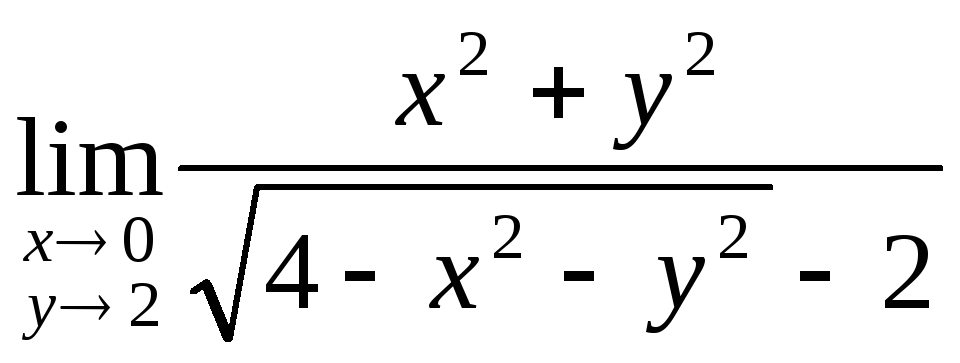
A) -4
B) 9
C) 18
D) -40
E)
7.
Вычислить предел
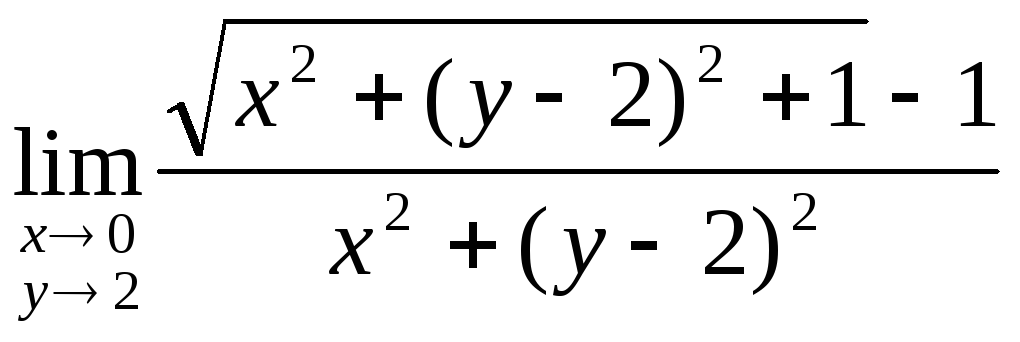
A)
B) 0
C)
D) 9
E) 20
8.
Функция
непрерывная
в каждой точке некоторой области
называется..
А)
непрерывной в области
B)
дифференцируемой в области
С)
ограниченной в области
D)
кусочно-непрерывной в области
E)
монотонной в области
9.
По формуле
вычисляется
А)
полный дифференциал функции
B)
частная производная от функции
по переменной
С)
частная производная от функции
по переменной у
D)
частный дифференциал функции
E)
частный дифференциал функции
10.
Полный дифференциал функции
вычисляется по формуле
A)
B)
C)
D)
E)
11.
Функция, имеющая дифференциал в каждой
точке некоторой области
называется
А)
дифференцируемой в области
B)
непрерывной в области
С)
кусочно-непрерывной в области
D)
убывающей в области
Е)
неограниченной в области
12.
Найти
функции
:
А)
В)
С)
D)
E) 30
13.
Найти
функции
:
А)
B)
С)
D)
E)
14.
Найти
функции
:
А)
B)
С)
D)
Е)
15.
Найти
функции
:
А)
B)
С)
D)
Е)
16.
Найти
функции
:
А)
B)
С)
D)
Е)
17.
Найти
функции
:
A)
B)
C)
D)
E)
18.
Найти
функции
:
А)
B)
С)
D)
Е)
19.
Найти
функции
:
А)
B)
C)
D)
E)
20.
Найти
функции
:
А)
B)
C)
D)
E)
21.
Если
-
дифференцируемая функция своих
аргументов
и
,
а
и
являются дифференцируемыми функциями
от аргумента
,
то производная сложной функции
находится по формуле:
A)
B)
C)
D)
E)
22.
Если
- дифференцируемая функция своих
аргументов
и
,
а
и
,
то частная производная
сложной функции
находится по формуле:
A)
B)
C)
D)
E)
23.
Если
- дифференцируемая функция своих
аргументов
и
,
а
и
,
то частная производная
сложной функции
находится по формуле:
A)
B)
C)
D)
E)
24.
Функция
называется неявной функцией от
и
,
если она задается уравнением..
A)
B)
C)
D)
E)
25.
Частной производной
неявной функции
:
A)
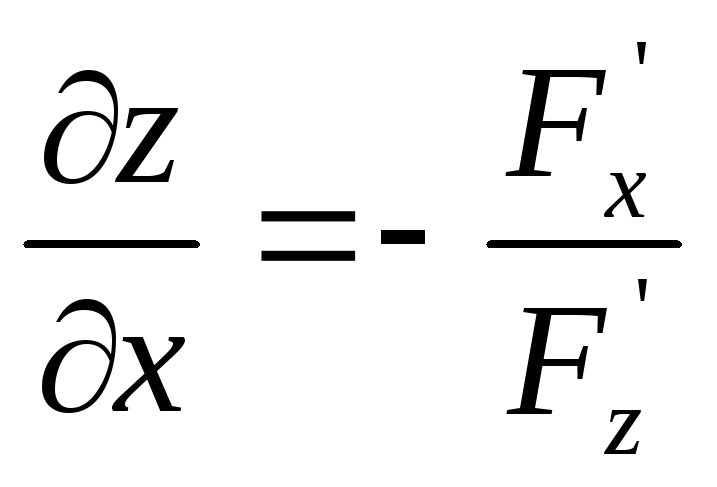
B)
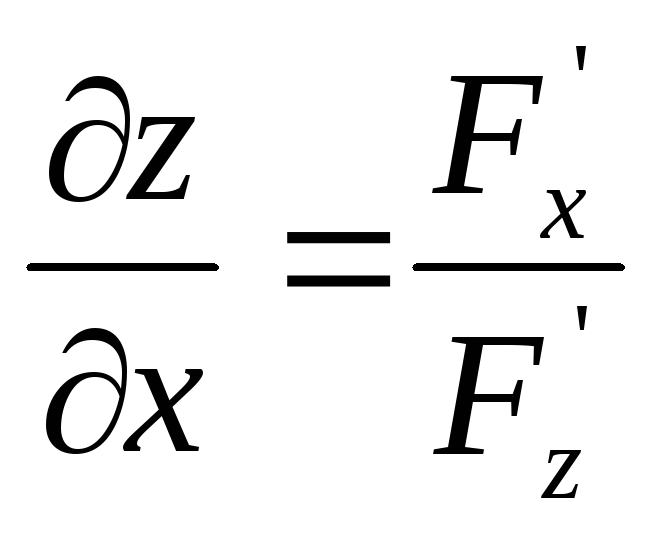
C)
D)
E)
26.
Указать формулу нахождения частной
производной
неявной функции
:
A)
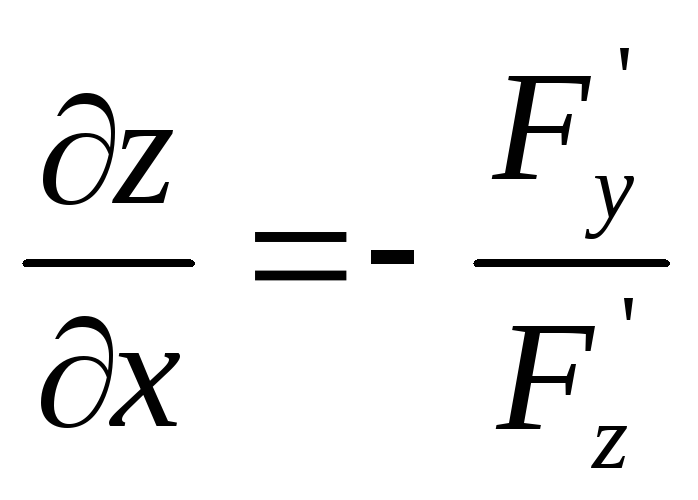
B)
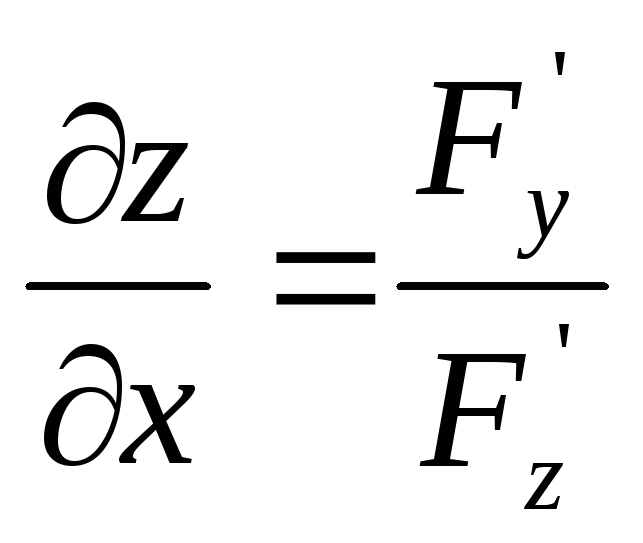
C)
D)
E)
27.
Указать неявные функции
:
A)
B)
C)
D)
E)
28.
Полный дифференциал неявной функции
находится по формуле:
A)
B)
C)
D)
E)
29.
Найти
функции
,
где
:
A)
B)
C)
D)
E)
30.
Найти
функции
,
где
:
A)
B)
C)
D)
E)
31.
Найти частную производную
сложной функции
,
где
,
:
A)
B)
C)
D)
E)
32.
Найти частную производную
сложной функции
,
где
,
:
A)
B)
C)
D)
E)
33.
Найти частную производную
сложной функции
,
если
,
:
A)
B)
C)
D)
E)
34.
Найти частную производную
сложной функции
,
если
,
:
A)
B)
C)
D)
E)
35.
Найти частную производную
сложной функции
,
если
:
A)
B)
C)
D)
E)
36.
Найти частную производную
сложной
функции
,
если
:
A)
B)
C)
D)
E)
37.
Найти частную производную
неявной функции
:
A)
B)
C)
D)
E)
38.
Найти частную производную
неявной функции
:
A)
B)
C)
D)
E)
39.
Найти частную производную
неявной функции
A)
B)
C)
D)
E)
40.
Найти частную производную
неявной функции
A)
B)
C)
D)
E)
41.
Найти
функции
:
A)
B)
C)
D)
E)
42.
Найти
функции
:
A)
B)
C)
D)
E)
43.
Найти
функции
A)
B)
C)
D)
E)
44.
Найти
функции
A)
B)
C)
D)
